Файл: Точек, являющихся образом множества объектов, и множества линий.docx

Остались не вычеркнутыми элементы:

l₀₁=7: l₀₅+l₅₁=13+10=23>7;

l₀₂=5: l₀₅+l₅₂=13+8=21>5;

l₀₃=3: l₀₅+l₅₃=13+2=15>3;

l₀₄=9:l₀₅+l₅₄=13+10=23>9;

l₀₆=8: l₀₅+l₅₆=13+7=20>8;

l₀₇=18: l₀₅+l₅₇=13+12=25>18;

l₁₂=2: l₁₅+l₅₂=10+8=18>2;

l₁₃=4: l₁₅+l₅₃=10+10=20>4;

l₁₄=6: l₁₅+l₅₄=10+10=20>6;

l₁₆=8: l₁₅+l₅₆=10+7=17>8;

l₁₇=15: l₁₅+l₅₇=10+12=27>15;

l₂₃=2: l₂₅+l₅₃=8+10=18>2;

l₂₄=4: l₂₅+l₅₄=8+10=18>4;

l₂₆=6: l₂₅+l₅₆=8+7=15>6;

l₂₇=13: l₂₅+l₅₇=8+12=20>13;

l₃₄=6: l₃₅+l₅₄=10+10=20>10;

l₃₆=5: l₃₅+l₅₆=10+7=17>5;

l₃₇=15: l₃₅+l₅₇=10+12=22>15;

l₄₆=10:l₄₅+l₅₆=10+7=17>10;

l₄₇=9: l₄₅+l₅₇=10+12=22>9;

l₆₇=10:l₆₅+l₅₇=7+12=19>10.

Очевидно, никаких изменений в обеих матрицах не следует.
р=6

L 6	x0	x1	x2	x3	x4	x5	x6	x7
x0	0	7	5	3	9	13	8	18
x1	7	0	2	4	6	10	8	15
x2	5	2	0	2	4	8	6	13
x3	3	4	2	0	6	10	5	15
x4	9	6	4	6	0	10	10	9
x5	13	10	8	10	10	0	7	12
x6	8	8	6	5	10	7	0	10
x7	18	15	13	15	9	12	10	0

---

Остались не вычеркнутыми элементы:

l₀₁=7: l₀₆+l₆₁=8+8=16>7;

l₀₂=5: l₀₆+l₆₂=8+6=14>5;

l₀₃=3: l₀₆+l₆₃=8+5=13>3;

l₀₄=9:l₀₆+l₆₄=8+10=18>9;

l₀₅=13: l₀₆+l₆₅=8+7=15>13;

l₀₇=18: l₀₆+l₆₇=8+10=18=18;

l₁₂=2: l₁₆+l₆₂=8+6=14>2;

l₁₃=4: l₁₆+l₆₃=8+5=13>4;

l₁₄=6: l₁₆+l₆₄=8+10=18>6;

l₁₅=10: l₁₆+l₆₅=8+7=15>10;

l₁₇=15: l₁₆+l₆₇=8+10=18>15;

l₂₃=2: l₂₆+l₆₃=6+5=11>2;

l₂₄=4: l₂₆+l₆₄=6+10=16>4;

l₂₅=6: l₂₆+l₆₅=6+7=13>6;

l₂₇=13: l₂₆+l₆₇=6+10=16>13;

l₃₄=6: l₃₆+l₆₄=5+10=15>6;

l₃₅=10: l₃₆+l₆₅=5+7=12>10;

l₃₇=15: l₃₆+l₆₇=5+10=15=15;

l₄₅=10:l₄₆+l₆₅=10+7=17>10;

l₄₇=9: l₄₆+l₆₇=10+10=20>9;

l₅₇=12:l₅₆+l₆₇=7+10=17>12.

Очевидно, никаких изменений в обеих матрицах не следует.
р=7

L7	x0	x1	x2	x3	x4	x5	x6	x7
x0	0	7	5	3	9	13	8	18
x1	7	0	2	4	6	10	8	15
x2	5	2	0	2	4	8	6	13
x3	3	4	2	0	6	10	5	15
x4	9	6	4	6	0	10	10	9
x5	13	10	8	10	10	0	7	12
x6	8	8	6	5	10	7	0	10
x7	18	15	13	15	9	12	10	0

1   ...   9   10   11   12   13   14   15   16   17

---

Остались не вычеркнутыми элементы:

l₀₁=7: l₀₇+l₇₁=18+15=33>7;

l₀₂=5: l₀₇+l₇₂=18+13=31>5;

l₀₃=3: l₀₇+l₇₃=18+15=33>3;

l₀₄=9:l₀₇+l₇₄=18+9=27>9;

l₀₅=13: l₀₇+l₇₅=18+12=30>13;

l₀₆=8: l₀₇+l₇₆=18+10=28>18;

l₁₂=2: l₁₇+l₇₂=15+13=28>2;

l₁₃=4: l₁₇+l₇₃=15+15=30>4;

l₁₄=6: l₁₇+l₇₄=15+9=24>6;

l₁₅=10: l₁₇+l₇₅=15+12=27>10;

l₁₆=8: l₁₇+l₇₆=15+10=25>15;

l₂₃=2: l₂₇+l₇₃=13+15=28>2;

l₂₄=4: l₂₇+l₇₄=13+9=22>4;

l₂₅=8: l₂₇+l₇₅=13+12=25>8;

l₂₆=6: l₂₇+l₇₆=13+10=23>6;

l₃₄=6: l₃₇+l₇₄=15+9=24>6;

l₃₅=10: l₃₇+l₇₅=15+12=27>10;

l₃₆=5: l₃₇+l₇₆=15+10=25>5;

l₄₅=10:l₄₇+l₇₅=9+12=21>10;

l₄₆=10: l₄₇+l₇₆=9+10=19>10;

l₅₆=7:l₅₇+l₇₆=7+10=17>12.

Очевидно, никаких изменений в обеих матрицах не следует.

Таким образом, результат решения задачи совпадает с результатом при р=4, поскольку последние изменения в прокладке кратчайших маршрутов для данного графа завершились после исследования x₄ в качестве базовой вершины:

L7

x0

x1

x2

x3

x4

x5

x6

x7

 7

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

7

5

3

9

13

8

18

x0

x0

x3

x3

x3

2x3

х3

х3

1x4

x1

7

0

2

4

6

10

8

15

x1

x3

x1

x2

x2

x2

x2

x2

x4

x2

5

2

0

2

4

8

6

13

x2

x3

x1

x2

x3

x4

x5

x6

x4

x3

3

4

2

0

6

10

5

15

x3

x0

x2

x2

x3

3x2

x2

x6

x4

x4

9

6

4

6

0

10

10

9

x4

x3

x2

x2

x2

x4

x5

x2

x7

x5

13

10

8

10

10

0

7

12

x5

x3

x2

x2

x2

x4

x5

x6

x7

x6

8

8

6

5

10

7

0

10

x6

x3

x2

x2

x3

x2

x5

x6

x7

x7

18

15

13

15

9

12

10

0

x7

x4

x4

x4

x4

x4

x5

x6

x7

---

По матрице ||L⁷(n, n)|| можно найти длину кратчайшего перехода между любой парой вершин исходного графа. Например, между вершинами х₀ и х₇длина кратчайшего перехода l₀₇=18, между вершинами х₁ и х₆ длина кратчайшего перехода l₁₆=8.

По матрице ||ν⁷(n, n)|| можно сформировать переход, соответствующий кратчайшему маршруту. Рассмотрим эту задачу на примере вершин х₀ и х₇ (вершины перехода выделены в результирующей матрице переходов зеленым цветом):

• 
  переход х₀ - х₇ выполняется через вершину х₄, смежную с вершиной х₇, – получаем фрагмент перехода (х₄, х₇) длиной 9;
  
• 
  переход х₀ – х₄ выполняется через вершину х₃, смежную с вершиной х₀, – получаем фрагмент перехода (х₀, х₃) длиной 3;
  
• 
  переход х₃ – х₄ выполняется через вершину х₂, смежную с обеими вершинами, – получаем фрагмент перехода (х₃, х₂, х₄) длиной 2+4=6.
  

В результате «соединения» фрагментов переходов получается переход ν₀₇=(х₀, х₃, х₂, х₄, х₇).

Для вершин х₁ и х₆ переход х₁ - х₆ выполняется через вершину х₂, смежную обеим вершинам, – сразу получаем результат - переход ν₁₆=(х₁, х₂, х₆).
При решении практических задач возникает необходимость поиска нескольких путей, частично упорядоченных по возрастанию относительно кратчайшего. Такие задачи возникают при врéменной загруженности канала на определенном участке или неисправности узла. Для решения подобных задач разработаны обобщенные алгоритмы Флойда, которые в данном курсе не рассматриваются.

---

3.4. Поиск критического пути в графе

Графовые моделичасто используются для управления некоторым проектом, например, учебным процессом.

Каждый проект имеет, как правило, большой перечень работ и большое число соисполнителей с указанием продолжительности и стоимости каждой работы, последовательности и согласованности исполнения. В случае учебного процесса эти работы включают:

1. 
   разработку основной образовательной программы по направлению подготовки,
   
2. 
   составление календарного плана;
   
3. 
   распределение учебной нагрузки между кафедрами и преподавателями;
   
4. 
   формирование расписания;
   
5. 
   обучение студентов;
   
6. 
   защиту выпускной квалификационной работы.
   

Для сложного проекта необходимо:

1. 
   устанавливать последовательность и сроки использования ограниченных ресурсов,
   
2. 
   координировать работы соисполнителей,
   
3. 
   анализировать компромиссные решения по затратам и срокам исполнения,
   
4. 
   предвидеть возможные срывы и задержки каждой работы и проекта в целом.
   

С целью управления проектами был разработан метод сетевого планирования и управления (СПУ), задача которого состоит в том, чтобы средствами графовых моделей наглядно и системно отобразить, исследовать и оптимизировать последовательность и взаимозависимость работ.

В качестве такой графовой модели используется ориентированный граф и разработанные методы и модели его анализа и исследования.

Граф, используемый в СПУ, имеет одну вершину–исток, которая представляет начало работ по всему проекту, и одну вершину–сток, которая представляет окончание всего проекта, т.е. является сетевой моделью.

На рисунке представлена упрощенная сетевая модель проекта:



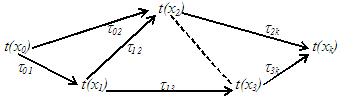
Между истоком сети x₀ и стоком сети x_kесть множество вершин–событий x₁, x₂, x₃, фиксирующих начало и/или окончание одной или нескольких работ в моменты времени t(x_i), а множество дуг – это работы, имеющие продолжительность τ

---