ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2190
Скачиваний: 4
УДК 004.42
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ДВИЖЕНИЯ
ОБЪЕКТОВ НА ПАНОРАМНЫХ СНИМКАХ
А.В. Войцеховский
Дальневосточный Федеральный Университет
Россия, 690091, Владивосток, Суханова 8
E-mail:
artvc@myopera.com
Ключевые слова:
компьютерное зрение, панорамные снимки, определение
параметров движения, определение пространственных характеристик
Введение
В современном мире очень часто появляются задачи автоматического слеже-
ния за местностью. Они относятся к классу задач компьютерного зрения. В этой
работе рассматривается проблема определения параметров движения объектов на
панорамных снимках акваторий, полученные стационарными поворотными каме-
рами. Для решения проблемы анализа снимков требовалось найти и разработать
алгоритмы, которые позволяют выяснить пространственные параметры движения
объектов, анализируя имеющуюся серию панорамных снимков. Целью работы стало
создание основанного на этих алгоритмах программного средства, которое анали-
зирует снимки местности, определяет движущиеся объекты и их характеристики:
расстояние до них, географические координаты, скорость и направление движения,
приблизительные размеры, а также строит горизонтальный снимок местности для
каждой фотографии камеры.
Рис. 1.
Структура объектов предметной области
1.
Анализ предметной области
В качестве ресурсов для разработки имеются панорамные снимки территорий
и акваторий, полученные стационарными поворотными камерами, подключенными
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
46
к сетям передачи данных. В процессе анализа предметной области были выделены
следующие объекты: камера, объект на снимке, снимок и модель Земли. С помо-
щью языка онтологий были формализованы приведенные объекты и описана их
структура и связи.
2.
Алгоритмы
Перед началом анализа изображения к нему применяется алгоритм бинариза-
ции. Используется адаптивная пороговая бинаризация, т.к. на снимках могут быть
различные тона в зависимости от погодных условий. Для выделения объектов на
снимках применяется алгоритм построения скелета объект [1]. Благодаря нахожде-
нию скелетов с помощью алгоритма восьми масок, скелеты объектов получаются
связными взвешенными графами. Это позволяет находить объект на разных сним-
ках, даже если он изменяет свое направление относительно предыдущего положе-
ния. Для определения расстояния до объекта используются коэффициенты прямого
линейного преобразования. С помощью них становится возможным соотносить ми-
ровые координаты и координаты изображения. Также для этого требуется знать
одну мировую координату точки на снимке, или высоту камеры [2, 3]. Необходи-
мо иметь данные об оптических характеристиках камеры: вертикальный и гори-
зонтальный углы обзора и фокусное расстояние. Для определения географических
координат объекта используется адаптированный метод Гельмерта [4]. Этот метод
по известным широте и долготе начальной точки, заданному азимуту и дистанции
до конечной точки находит ее широту и долготу. Система должна преобразовывать
наклонные снимки, которые создаются береговыми стационарными поворотными
камерами, в горизонтальные. В фотограмметрии это решается с помощью метода
трансформирования координат [5, с. 67].
3.
Проектирование и реализация
3.1.
Проект
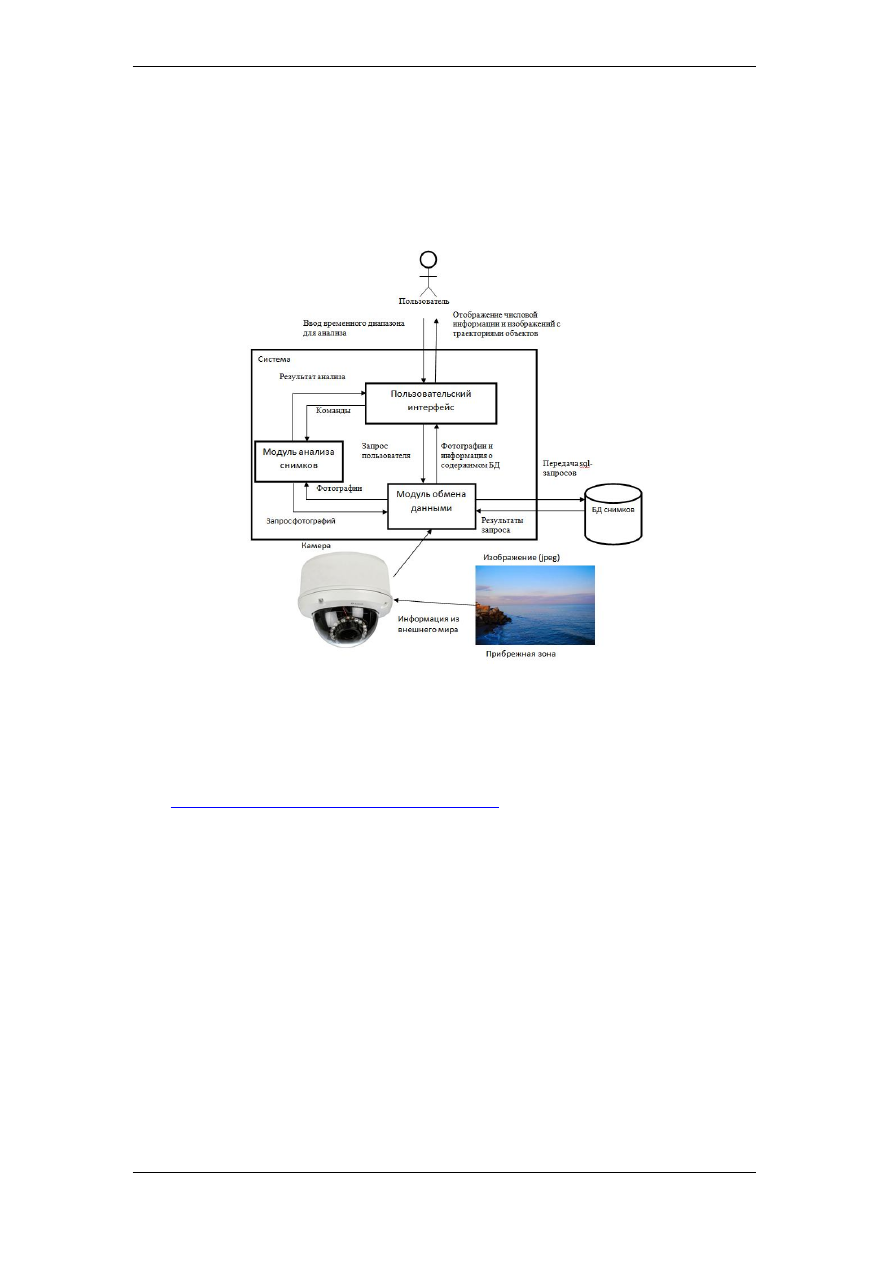
Составлена архитектурно-контекстная диаграмма программного средства (рис.
2). Архитектурно-контекстная диаграмма представляет схему взаимодействия ком-
понентов системы между собой, а так же схему взаимодействия пользователя с си-
стемой.
3.2.
Средства реализации
В качестве языка реализации выбран C++, так как C++ программы отлича-
ются высокой производительностью. Для разработки модуля анализа изображений
используется библиотека компьютерного зрения OpenCV 4.4. Она содержит сред-
ства для доступа к данным изображений, преобразования их в различные фор-
маты. Включая в себя большое множество различных операций преобразования
цифровых снимков библиотека исключает необходимость реализации многих функ-
ций, ускоряя разработку. так же преимуществом OpenCV является использование
оттестированных и оптимизированных функции обработки цифровых снимков. В
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
47
качестве СУБД выбран MySQL 5.6. Причиной выбора стала поддержка MySQL
реляционной модели данных. Так как в базе данных не предполагается хранить
больших объемов информации, то MySQL полностью подходит для реализации дан-
ного программного средства. В результате была спроектирована система, которая
использует перечисленные методы для определения параметров движения объек-
тов на серии панорамных снимков. На реальных снимках опробованы алгоритмы
бинаризации, выделения и сравнения скелетов объектов.
Рис. 2.
Архитектурно-контекстная диаграмма
Список литературы
1.
Выделение и анализ скелетов объектов на цветных снимках.
http://swsys.ru/index.php?page=article&id=2198
.
2.
R. A. Holman, T. C. Lippmann, P. V. O’Neill, and K. Hathaway, “Video estimation of
subaerial beach pro?les” // Marine Geology. 1991. Vol. 97, P. 225–231.
3.
R. A. Holman, A. H. Sallenger, Jr., T. C. Lippmann, and J. W. Haines, “The application of
video image processing to the study of nearshore processes” // Oceanography. 1993. Vol.
6, P. 85, P. 78–85
4.
Charles F. F. Karney Algorithms for geodesics SRI International / 201 Washington Rd,
Princeton, NJ 08543-5300, USA, P. 43–46.
5.
Назаров А.С. Фотограмметрия: учебное пособие для студентов вузов. Мн.: ТетраСи-
стемс, 2006. 368с.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
УДК 51-76:57.03
МОДЕЛИРОВАНИЕ ПЛАНКТОННОГО
СООБЩЕСТВА С УЧЕТОМ
ВЕРТИКАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
ЗООПЛАНКТОНА
Е.Е. Гиричева
Институт автоматики и процессов управления ДВО РАН
Россия, 690041, Владивосток, Радио 5
E-mail:
evg.giricheva@yandex.ru
Ключевые слова:
математическое моделирование, трофические взаимо-
действия
В работе моделируется взаимодействие фитопланктона и зоопланктона в
вертикальном столбе воды. Динамика сообщества рассматривается с учетом
активных перемещений популяции зоопланктона, обусловленных суточной
вертикальной миграцией и таксисом.
Введение
При моделировании взаимодействия планктонного сообщества необходимо учи-
тывать неоднородность распределения популяций по глубине. Перемещение особей
связано с пассивным движением, вызванным диффузией, а также активными пе-
ремещениями зоопланктона. Они могут быть обусловлены различными причинами,
среди которых суточные вертикальные миграции и таксис. Зоопланктон совершает
суточные перемещения, поднимаясь ночью к поверхности, а днем опускаясь на глу-
бину. Это связано с уходом в светлое время суток от хищников [1,2,3,4,5]. Таксис -
это активные перемещения хищника в направлении жертвы. В работе рассматрива-
ется взаимодействие популяций планктона под влиянием активных вертикальных
перемещений зоопланктона. Исследуется влияние суточных миграций и таксиса на
распределение популяций в вертикальном столбе воды и динамику их биомассы.
1.
Описание модели
Рассмотрим модель взаимодействия фитопланктона (P) и зооплантона (Z) с
учетом биогенов (N) в верхнем перемешанном слое воды. Пассивные перемещения
компонентов описываются турбулентной диффузией с коэффициентами
D
1
, D
2
, D
3
.
Активное движение зоопланктона по глубине представлено суточными миграция-
ми со скоростью
v
(
t, x
)
и таксисом -
∂
∂x
(
w
(
t, x
)
Z
∂P
∂x
)
, который описывается в соот-
ветствии с предположением о пропорциональности скорости перемещения хищника
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
49
градиенту плотности популяции жертв [6,7,8,]. Изменение плотности биомассы ком-
понент опишем системой дифференциальных уравнений типа "реакция-адвекция-
диффузия":
∂N
∂t
=
D
1
∂
2
N
∂x
2
+
Q
1
(
N
0
−
N
1
) +
β
(
m
P
P
+
m
Z
Z
+
γZ
2
)
−
µ
P
N
K
N
+
N
P
;
∂P
∂t
=
D
2
∂
2
P
∂x
2
+
µ
P
N
K
N
+
N
P
−
µ
Z
P
K
P
+
P
Z
−
(
m
P
+
Q
2
)
P
;
∂Z
∂t
=
D
2
∂
2
Z
∂x
2
−
v
(
t, x
)
∂Z
∂x
−
∂
∂x
(
w
(
t, x
)
Z
∂P
∂x
)+
+
µ
Z
P
K
P
+
P
Z
−
γZ
2
−
(
m
Z
+
Q
3
)
Z.
(1)
Изменение концентрации биогенов в каждой точке области происходит за счет под-
тока и одтока вещества со скоростью
Q
1
, реминерализации отмершей органики с ко-
эффициентом
β
и потребления фитопланктоном, описываемого функцией Михаэли-
са-Ментен с параметрами:
µ
P
- максимальная скорость роста фитопланктона и
K
N
-
константа полунасыщения фитопланктона по биогенам. Увеличение биомассы фи-
топланктона происходит в процессе фотосинтеза при участии биогенов, а убыль - в
результате выедания зоопланктоном (функция Холлинга с параметрами:
µ
Z
- мак-
симальная скорость выедания зоопланктоном фитопланктона и
K
P
- константа по-
лунасыщения зоопланктона), естественной смертности (
m
P
- удельная смертность)
и вымывания из рассматриваемой области со скоростью
Q
2
. Биомасса зоопланктона
растет за счет выедания фитопланктона и убывает из-за естественной смертности
(
m
Z
- удельная смертность), выедания рыбами и другими организмами, не учтен-
ными в модели, а также внутривидовой конкуренции (с удельной скоростью
γ
) и
вымывания со скоростью
Q
3
. В качестве пространственной области будем рассмат-
ривать отрезок [0,1].Граничные условия означают изолированность рассматривае-
мого трофического сообщества:
∂N
∂x
(
t,
0) =
∂N
∂x
(
t,
1) = 0
,
∂P
∂x
(
t,
0) =
∂P
∂x
(
t,
1) = 0
,
∂Z
∂x
(
t,
0) =
∂Z
∂x
(
t,
1) = 0
.
2.
Численные расчеты
Время измеряем в сутках, все моделируемые компоненты рассматриваются в
единицах азота:
mmol N m
−
3
. Исходя из литературных данных [9,10], определяются
значения основных параметров системы (1):
β
= 0
.
2
,
α
= 0
.
75
,
γ
= 0
.
3
,
K
N
= 0
.
5
,
K
P
= 1
,
m
P
= 0
.
08
,
m
Z
= 0
.
02
,
Q
1
=
Q
2
=
Q
3
= 0
.
01
,
N
0
= 10
,
¯
µ
P
= 1
,
µ
Z
= 0
.
5
.
Неоднородность распределения фитопланктона по глубине учтем, определив коэф-
фициент роста как функцию глубины:
µ
P
= ¯
µ
P
e
−
δx
.
Для численного решения задачи (1) использована неявная конечноразностная схема
второго порядка точности по x и первого по t. Полагаем, что зоопланктон находится
у поверхности первые 4 часа суток, затем в течение 8 часов опускается на глубину
и через 4 часа вновь в течение 8 часов поднимается к поверхности. Рассмотрим
следующие варианты поведения зоопланктона.
Вариант 1
. Таксис только ночью,
хищничество - весь день.
Вариант 2
. И таксис, и хищничество - только ночью.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.