ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2192
Скачиваний: 4
55
Обозначим за
h
= [
h
1
(0)
, . . . , h
1
(
n
1
)
, . . . , h
N
(0)
, . . . , h
N
(
n
N
)]
T
вектор, объединя-
ющий импульсные характеристики, вносящие вклад от каждого входного воздей-
ствия, за
u
= [
u
1
(
t
)
, . . . , u
1
(
t
−
n
1
)
, . . . , u
N
(
t
)
, . . . , u
N
(
t
−
n
N
)]
T
- вектор, объединя-
ющий соответствующие, из уравнения(5),
h
значения входных воздействий. Урав-
нение (5) перепишется в виде:
y
=
u
T
h
(6)
Количество коэффициентов в векторе
h
равно
N
P
k
=1
n
k
, соответственно, при наличии
N
P
k
=1
n
k
измерений выхода y уравнение (6) можно записать в векторно-матричной
форме:
Y
=
Uh
,
(7)
где
Y
- вектор, содержащий измерения выхода
y
, а
U
- матрица, содержащая из-
меренные входы
u
, соответствующие определенному выходу
y
из (5). Из (7)можно
найти
h
:
h
=
U
−
1
Y
(8)
Полученные значения импульсных характеристик верны при отсутствии шумов,
но в реальных условиях такая ситуация встречается очень редко. Для преодоле-
ния проблемы зашумленности и более точной оценки импульсных характеристик
используется рекуррентное оценивание [5]. За начальное условие для рекуррент-
ного оценивания принимается значение
h
, полученное из (8). По последующим
измеренным значениям выхода
y
i
=
y
i
(
t
)
и соответствующим ему входам
u
i
=
[
u
1
(
t
)
, . . . , u
1
(
t
−
n
1
)
, . . . , u
N
(
t
)
, . . . , u
N
(
t
−
n
N
)]
T
, не участвовавшим в определе-
нии
h
из (8), получаем уравнение модели объекта в блочном виде [6]:
"
Y
i
−
1
y
i
#
=
"
U
i
−
1
u
T
i
#
h
i
+1
и в итоге алгоритм рекуррентного оценивания имеет вид:
P
i
=
U
T
i
−
1
U
i
−
1
−
1
,
P
i
+1
=
P
i
−
P
i
u
i
u
T
i
P
i
u
i
+ 1
−
1
u
T
i
P
(9)
,
h
i
+1
=
h
i
+
P
i
+1
u
i
y
i
−
u
T
i
h
i
(10)
Формулы (9)-(10) позволяют вычислить новую оценку параметров
h
i
+1
, если за-
даны: a) предыдущие оценки параметров
h
i
и оценки
P
i
; b) новая информация
об измерениях
u
T
i
,
y
i
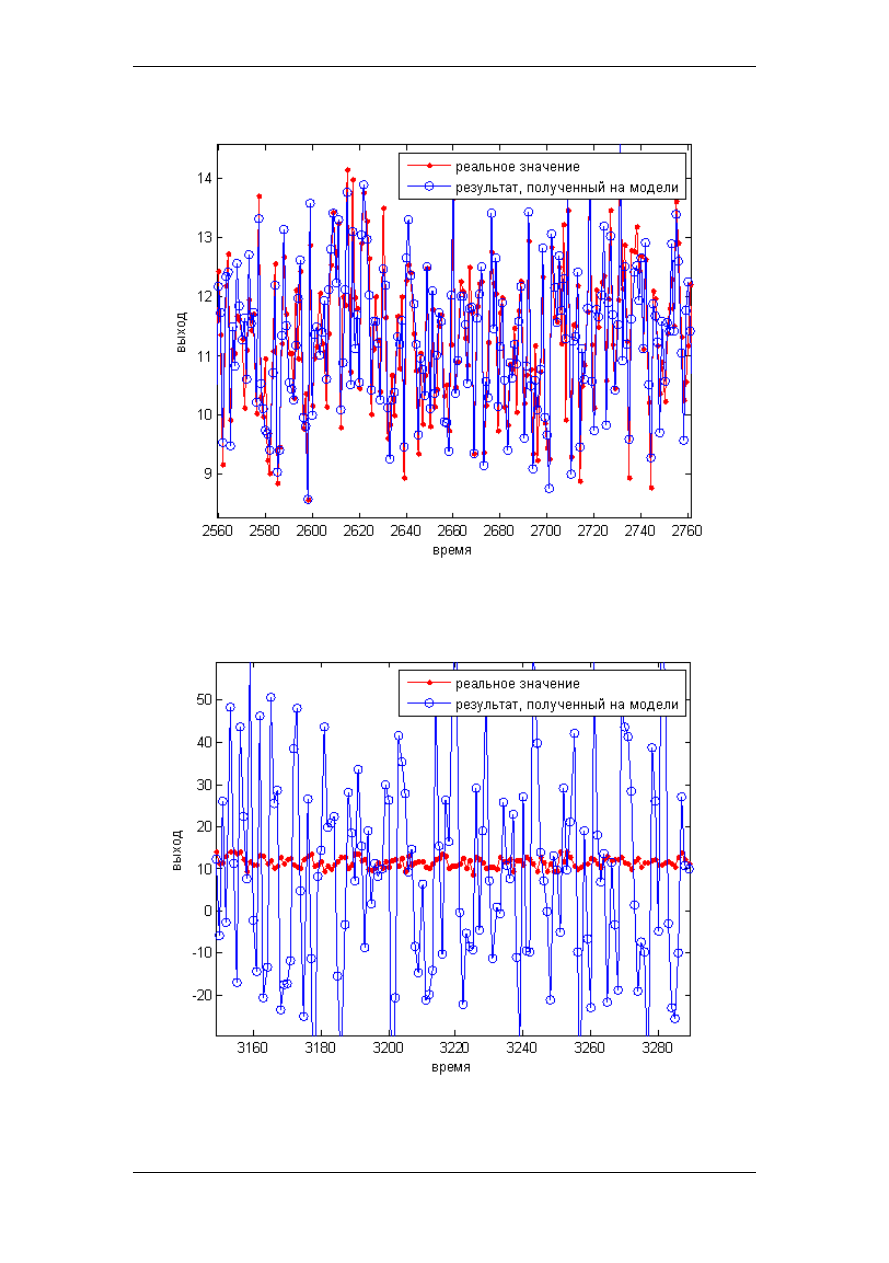
. На рис. 2 представлен результат применения описанного
алгоритма определения импульсной характеристики, смоделированной в системе
MATLAB. Для получения выборок входящих воздействий и выхода использовался
объект управления, описывающийся уравнением:
y
=
0
.
1813
z
−
0
.
1887
u
1
+
1
.
984
z
−
0
.
7165
u
2
Помехи на выходе генерировались случайным образом из диапазона от 0 до 1. Глу-
бина модели для импульсных характеристик от обоих входов
n
= 40
. В реальных
условиях глубина модели заранее неизвестна, но при выборе
n
больше реального
значения, значения импульсной характеристики вычисляются с той же точностью,
но с большими временными затратами на вычисления. Значения выхода, вычис-
ленного без использования рекуррентного оценивания, с помощью уравнения (8)
представлены на рис. 3.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
56
Рис. 2.
Результат применения описанного алгоритма
Рис. 3.
Значения выхода, вычисленного без
использования рекуррентного оценивания
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
57
Заключение
Предложенная процедура оценивания импульсной характеристики может быть
легко реализована в реальных условиях. В используемом алгоритме идентификации
отсутствует необходимость применять специальные тестовые сигналы, а достаточ-
но наличия результатов пассивного эксперимента. В дальнейшем планируется рас-
пространение предложенного алгоритма на случай влияния внешних неизмеряемых
возмущений различного типа.
Список литературы
1.
Дилигенская А.Н. Идентификация объектов управления. - Самара: Самарский го-
сударственный технический университет, 2009. 136с.
2.
Бокс Д., Дженкинс Г. Анализ временных рядов. Прогноз и управление. - М.: Мир,
1974. Вып. 1. 406с.
3.
Гроп Д. Методы идентификации систем. - М.: Мир, 1979, 302с.
4.
Ли Р. Оптимальные оценки, определение характеристик и управление. - М.: Наука,
1966. 190с.
5.
Сейдж Эндрю П., Мелса Джеймс Л. Идентификация систем управления. - М.Наука,
1974. 248с.
6.
Кафедра «Автоматика и телекоммуникации». Опорный конспект по курсу «Моде-
лирование и идентификация объектов систем автоматики». - Донецк: Донецкий Го-
сударственный Технический Университет, 2007. 31с.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
УДК 51-76
ИССЛЕДОВАНИЕ СВОЙСТВ РЕШЕНИЙ
В МОДЕЛИ МИКРОБИОЛОГИЧЕСКОЙ
ДИНАМИКИ
Г.В. Гренкин
Дальневосточный федеральный университет
Россия, 690950, Владивосток, Суханова 8
E-mail:
glebgrenkin@gmail.com
Ключевые слова:
фитопланктон, математическая модель, дифференци-
альные уравнения, равновесные решения, СЛАУ, метод Гаусса
В работе рассматривается математическая модель, описывающая динами-
ку численности сообщества видов фитопланктона, конкурирующих за пита-
тельные вещества. Модель представляет собой систему дифференциальных
уравнений. Описан алгоритм поиска равновесных решений системы диф-
ференциальных уравнений. Описан алгоритм решения системы линейных
алгебраических уравнений для случая, когда матрица системы может быть
квадратной вырожденной либо прямоугольной.
Введение
Фитопланктон составляет основу жизни в водоемах. Биопродуктивность вод-
ной экосистемы определяется продукцией фитопланктона. Изучение фитопланкто-
на позволяет понять наиболее масштабные процессы в экосистемах. В свою очередь,
фитопланктон в наибольшей степени зависит от питательных минеральных веществ
(биогенов). При изучении состояния и функционирования фитопланктона важную
роль в настоящее время играют данные дистанционных методов зондирования по-
верхности морей и океанов. В частности, искусственные спутники Земли позволяют
получить данные о содержании минеральных веществ и хлорофилла в поверхност-
ном слое. Данные о хлорофилле дают возможность оценить содержание фитопланк-
тона и дать грубую оценку первичной продукции. Данные о минеральных веществах
(на основе азота, фосфора, кремния и других химических элементов), составляю-
щих материальную основу для построения растительных организмов в процессе фо-
тосинтеза, дают возможность оценить характеристики продукционных процессов
фитопланктона. На этом этапе полезны математические модели динамики числен-
ностей (биомасс) основных видов фитопланктонного сообщества. В данной работе
рассматривается математическая модель, описывающая динамику численности со-
общества видов фитопланктона, конкурирующих за питательные вещества. Подоб-
ные математические модели используются также в описании динамики микробных
культур в лабораторных экспериментах. Модель представляет собой систему нели-
нейных дифференциальных уравнений. Рассматриваются уравновешенные стацио-
нарные решения, далее называемые равновесиями. Оказывается, что эти решения
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
59
достаточно подробно характеризуют фазовый портрет системы дифференциальных
уравнений. Разработана программная система, в которой реализован предложенный
в [1] алгоритм поиска равновесий. Разработан модуль для решения СЛАУ методом
Гаусса для случая, когда матрица системы может быть квадратной вырожденной
или прямоугольной.
1.
Математическая модель
В модели выделены биологические виды фитопланктона и группы минераль-
ных питательных веществ. Фитопланктон представлен
m
видами, их концентрации
в среде обозначены
y
i
для вида
i
. Минеральное питание растительных организмов
разбивается на
n
групп сходных веществ (на основе азота, фосфора, кремния и
т.п.). Питательные вещества предполагаются не взаимозаменяемыми. Содержание
веществ типа
j
в среде обозначается
z
j
, их содержание в клетке вида
i
обозна-
чается через
q
ij
. Эту величину называют клеточной квотой. В водоеме в летний
период фитопланктон обитает в верхней части столба воды, выше скачка темпера-
туры и плотности, называемого термоклином. Минеральные питательные вещества
поступают снизу под влиянием процессов разной природы, с такой же скоростью
содержимое верхней части водного столба в силу несжимаемости воды выбывает
из наблюдаемой зоны. В этом случае можно использовать данную модель, усред-
няя все характеристики по пространству. Концентрации фитопланктона и биогенов
будем измерять в г
/
м
3
, внутриклеточные концентрации питательного вещества в
г вещества
г сырой массы фитопланктона
, а время в сутках. Для живого организма та или
иная стратегия деятельности определяется не только окружающей средой, но и его
состоянием. Внутреннее состояние организма можно характеризовать по-разному.
В нашем случае как индикатор предлагается использовать внутриклеточное содер-
жание питательных веществ на основе минеральных соединений во внешней среде
— клеточную квоту
q
ij
. Потребление пищи микроорганизмами осуществляется с
удельной скоростью
v
ij
(
z
j
, q
ij
)
, а рост биомассы происходит с удельной скоростью
µ
ij
(
q
ij
)
при возможном ограничении, сформулированном как принцип «узкого ме-
ста» Либиха. Этот принцип считается дискуссионным, но в ряде ситуаций он лучше
других объясняет процессы роста биомассы вида. Скорость роста отдельного вида,
согласно принципу Либиха, ограничена скоростью роста наименее производительно-
го субстрата (биогена). Модель динамики масс компонентов системы приобретает
форму
dy
i
dt
=
min
j
=1
,...,n
µ
ij
(
q
ij
)
−
D
y
i
,
dz
j
dt
=
D
(
z
(0)
j
−
z
j
)
−
m
X
i
=1
v
ij
(
z
j
, q
ij
)
y
i
,
dq
ij
dt
=
v
ij
(
z
j
, q
ij
)
−
q
ij
·
min
j
=1
,...,n
µ
ij
(
q
ij
)
(1)
для
i
= 1
, . . . , m
,
j
= 1
, . . . , n
. Через
D
обозначена скорость протока вещества в
системе, через
z
(0)
j
— содержание минеральных питательных веществ во входящем
потоке. Конкретизация функций модели (1) в приложениях осуществляется на ос-
нове формулы М. Друпа для удельной скорости роста организмов:
µ
ij
(
q
ij
) =
µ
(0)
ij
1
−
q
ij
q
ij
.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.