ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2212
Скачиваний: 4
125
β
= 0
.
005
системы (2)) синхронизация колебаний наступает через временя
t
= 1800
(103.5 периодов для первого сообщества и 102 периода для второго). На языке нели-
нейной динамики говорят о различной длине переходного процесса к устойчивому
синхронному состоянию [3]. В системе устанавливаются стационарные колебания,
соответствующие движению фазовой точки вдоль предельно цикла (рис. 1). Значе-
ния системы на фазовых портретах обоих сообществ, начиная с указанного момента
времени, совпадают, что так же указывает на полную синхронизацию. Точкой си-
него (красного) цвета на рис. 1 обозначены начальные условия, черного цвета –
значение системы в рассматриваемый момент времени. Стрелками указано направ-
ление движения по фазовой кривой. С течением времени моментальные значения
Рис. 1.
Фазовый портрет системы (2) при
β
= 0
.
005
численности особей и фазы колебаний сближаются, разность фаз стремится к ну-
лю (точки фазовой кривой начинают двигаться по одной траектории), при этом,
разность моментальных амплитуд через указанный промежуток времени падает до
нуля (рис. 2). Возникает полная взаимная синхронизация колебаний, то есть, рас-
сматриваемые сообщества в равной степени воздействуют друг на друга и взаимно
подстраивают свои ритмы. На графиках, соответствующих фигурам Лиссажу вид-
но, что из асинхронного режима развитие сообществ переходит в квазипериодиче-
ский, затем колебания через указанный промежуток времени начинают синхронизи-
роваться, графики приближаются и сливаются с прямой, которая является биссек-
трисой угла и соответствует полной синхронизации колебаний (рис. 3). С увеличе-
нием значений параметра связи синхронизация наступает намного раньше. Очень
сильная связь стремиться сделать состояния обоих осцилляторов идентичными. В
процессе увеличения относительной доли миграции, можно выделить предельное
значение (
β
= 0
.
4)
, в котором синхронизация наступает максимально быстро (на
втором периоде (рис. 4)), при переходе через это значение количество периодов до-
стижения синхронизации увеличивается. Фигуры Лиссажу соответствует ситуации,
когда частоты и периоды колебаний через небольшой промежуток времени (
t
= 25
)
полностью совпадают - наступает полная взаимная синхронизация (биссектриса уг-
ла на фазовом портрете (рис. 5)). В этом случае полная взаимная синхронизация
колебаний наблюдается уже на втором периоде колебаний, т.е. фазовые портреты
полностью совпадают через отрезок времени
t
= 25
. Через указанный период вре-
мени две траектории сливаются в одну и только спустя время
t
= 60
получившаяся
кривая приближается к предельному циклу и сливается с ним (рис. 6).
3.
Выводы
Таким образом, показано, что введение коэффициента миграции в модель Базы-
кина типа «ресурс-потребитель», который является параметром связи между двумя
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
126
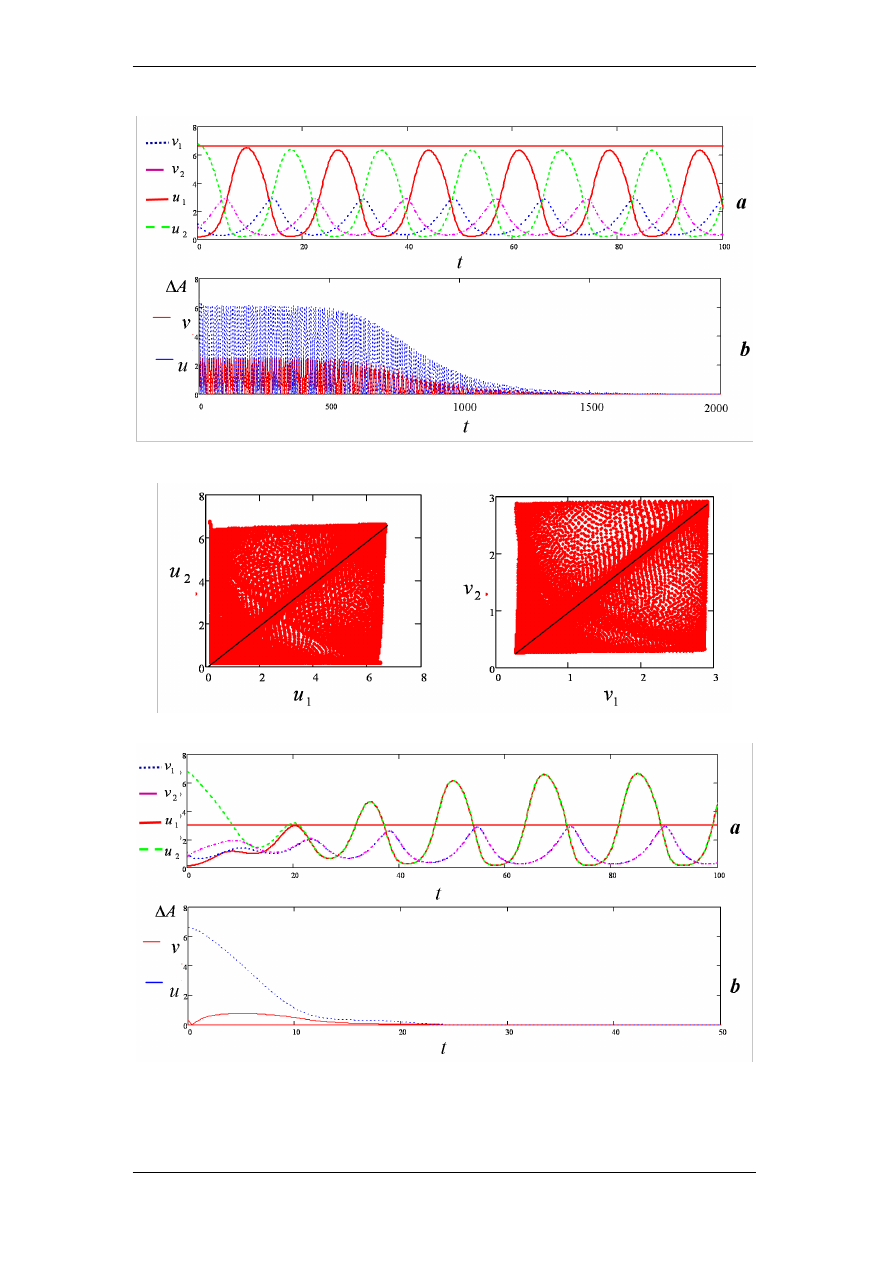
Рис. 2.
a) динамика системы (2) при
β
= 0
.
005
, b) разности моменталь-
ных амплитуд двух не связанных сообществ
Рис. 3.
Фигуры Лиссажу системы (2) при
β
= 0
.
005
Рис. 4.
a) динамика системы (2) при
β
= 0
.
4
, b) график разности момен-
тальных амплитуд двух рассматриваемых сообществ
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
127
Рис. 5.
Фигуры Лиссажу системы (2) при
β
= 0
.
4
Рис. 6.
Фазовый портрет системы (2) при
β
= 0
.
4
подобными соседними сообществами, приводит к синхронизации колебаний рассмат-
риваемых систем. От величины данного коэффициента зависит скорость синхрони-
зации этих систем (с увеличением значений
β
синхронизация наступает быстрее).
Найдено максимальное значение относительной доли миграции, соответствующее
наиболее быстрой синхронизации колебаний рассматриваемых сообществ, при пере-
ходе через которое время достижения полной синхронизации увеличивается.
Иссле-
дования проведены при финансовой поддержке РФФИ (региональный проект 11-01-
98512-р_восток_а).
Список литературы
1.
Базыкин А.Д.. Математическая биофизика взаимодействующих популяций. М., На-
ука, 1985.- 181с.
2.
Ризниченко Г.Ю. Математические модели в биофизике и экологии. Москва-Ижевск,
ИКИ, 2003, -184 с.
3.
Пиковский А. Розенблюм М. Куртс Ю. Синхронизация. Фундаментальное нели-
нейное явление. Пер.с англ. А.С. Пиковского, М.Г.Розенблюма.-М. ТЕХНОСФЕРА,
2003.-496с.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
УДК 519.2
О ПРОБЛЕМАХ ПРИБЛИЖЕННОГО
ВЫЧИСЛЕНИЯ МОМЕНТОВ И
ВОССТАНОВЛЕНИЯ ФУНКЦИИ
РАСПРЕДЕЛЕНИЯ ВЕРХНЕЙ
ЛЕСТНИЧНОЙ ВЫСОТЫ
Т.В. Лазовская
ВЦ ДВО РАН
Россия, 680000, Хабаровск, Ким-Ю-Чена, 65
ИПММ ФГБОУ ВПО "СПбГПУ"
Россия, 195251, Санкт-Петербург, Политехническая, 29
E-mail:
tatianala@list.ru
С.В. Нагаев
Институт математики им. С.Л. Соболева СО РАН
Россия, 630090, Новосибирск, Коптюга, 4
E-mail:
nagaev@math.nsc.ru
Ключевые слова:
метод моментов, лестничная высота, непрерывная
дробь, формула Бруно, уравнение Фробениуса, числа произвольной точно-
сти
Рассматривается задача приближенного вычисления моментов и функции
распределения верхней лестничной высоты. Предложены алгоритмы для
вычисления моментов по формулам из [5], в том числе поиска решений урав-
нения Фробениуса. Для восстановления функции распределения применя-
ется метод П.И. Чебышева, основанный на непрерывных дробях. Решается
проблема вычислений с произвольной точностью.
О методе моментов
Пусть известны и конечны первые
2
m
моментов
b
k
=
b
Z
a
x
k
f
(
x
)
dx, k
=0
,
1
, . . . ,
2
m
−
1
,
вероятностного распределения с плотностью
f
(
x
)
. В работе [1] П.Л. Чебышев полу-
чает решение для задачи приближенного вычисления соответствующей функции
распределения
F
(
v
) =
v
Z
a
f
(
x
)
dx,
a < v < b.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
129
Введем вспомогательные понятия. Непрерывной дробью будем называть выражение
вида
a
0
+
1
a
1
+
1
a
2
+
...
,
(1)
где
a
0
, a
1
, . . .
– конечная или бесконечная последовательность. Конечная непре-
рывная дробь
V
n
W
n
=
a
0
+
1
a
1
+
1
a
2
+
...
+
1
a
n
называется
n
-ой (порядка
n
) подходящей дробью для непрерывной дроби (1). При
этом
V
n
называют числителем, а
W
n
– знаменателем
n
-й подходящей дроби. В ра-
ботах [1] – [3] П.Л.Чебышев раскладывает функцию
P
2
m
−
1
k
=0
b
k
z
k
+1
в непрерывную
J
-дробь с подходящими дробями специального вида
ϕ
k
(
z
)
ψ
k
(
z
)
=
1
α
1
z
+
β
1
+
1
α
2
z
+
β
2
+
...
+
1
α
k
z
+
β
k
,
где
α
i
, β
i
– вещественные числа. Рассматривая для каждого фиксированного
v
функции аргумента
z
Φ
0
(
z
) =
ϕ
m
(
z
)
Z
(
z
)
−
ϕ
m
−
1
(
z
)
,
Φ
1
(
z
) =
ψ
m
(
z
)
Z
(
z
)
−
ψ
m
−
1
(
z
)
,
(2)
Z
(
z
) = (
z
−
v
)
γ
+
ψ
m
−
1
(
v
)
ψ
m
(
v
)
,
(3)
где
γ
= max
1
a
−
v
ψ
m
−
1
(
a
)
ψ
m
(
a
)
−
ψ
m
−
1
(
v
)
ψ
m
(
v
)
,
1
b
−
v
ψ
m
−
1
(
b
)
ψ
m
(
b
)
−
ψ
m
−
1
(
v
)
ψ
m
(
v
)
,
(4)
П.Л.Чебышев доказал, что
F
(
v
)
−
E
v
a
−
0
Φ
0
(
z
)
Φ
1
(
z
)
<
1
2
Φ
0
(
v
)
Φ
0
1
(
v
)
,
(5)
под
E
v
a
−
0
g
(
z
)
подразумевается сумма вычетов функции
g
(
z
)
в особых точках, при-
надлежащих интервалу
[
a, v
)
. Таким образом, имеем следующую схему приближен-
ного вычисления функции распределения: найти функции
Φ
i
(
z
)
по формулам (2) –
(4), затем корни многочлена
Φ
1
(
z
)
и сумму вычетов из (5). Числитель и знаменатель
подходящих дробей вычисляются по формулам из теоремы 7.15 книги [6],
ψ
n
(
z
) =
1
H
(1)
n
b
0
b
1
· · ·
b
n
b
1
b
2
· · ·
b
n
+1
·
·
· · ·
·
b
n
−
1
b
n
· · ·
b
2
n
−
1
1
z
· · ·
z
n
,
(6)
где
H
(1)
n
=
b
0
b
1
· · ·
b
n
−
1
b
1
b
2
· · ·
b
n
·
·
· · ·
·
b
n
−
1
b
n
· · ·
b
2
n
−
2
, n
= 1
,
2
, . . . .
(7)
ϕ
n
(
z
) =
ψ
n
(
z
)
b
0
z
+
b
1
z
2
+
· · ·
+
b
2
n
−
1
z
2
n
+
γ
(
n
)
2
n
z
2
n
+1
+
· · ·
.
(8)
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.