ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 06.04.2021
Просмотров: 2223
Скачиваний: 4
УДК 519.688
ПАРАЛЛЕЛЬНЫЙ ВЫЧИСЛИТЕЛЬНЫЙ
АЛГОРИТМ УЛУЧШЕНИЯ КАЧЕСТВА
ГИДРОАКУСТИЧЕСКИХ ИЗОБРАЖЕНИЙ
А.А. Сущенко
Дальневосточный федеральный университет
Россия, 690091, Владивосток, Октябрьская 27
E-mail:
fon_shtirlits@mail.ru
А.Е. Ковтанюк
Институт прикладной математики ДВО РАН
Россия, 690041, Владивосток, Радио 7
Дальневосточный федеральный университет
Россия, 690091, Владивосток, Октябрьская 27
E-mail:
ankov@imcs.dvgu.ru
Ключевые слова:
компьютерное моделирование, подводная робототехни-
ка, интерполяционные формулы, MPI
Предлагается параллельный алгоритм метода двойной фильтрации улучше-
ния качества гидроакустических изображений. Исследуется эффективность
предложенного алгоритма.
Введение
К настоящему времени на базе Института проблем морских технологий ДВО
РАН создан ряд автономных необитаемых подводных аппаратов (АНПА), прошед-
ших государственную сертификацию в соответствии со стандартом ISO-9001. С их
помощью решается целый ряд задач: картографирование дна, обзорно-поисковые
работы, мониторинг участков дна и мониторинг состояния подводных сооружений
(трубопроводов, кабель-трасс и т.д.). Подобные работы ведутся уже более 40 лет,
и до сих пор актуальной является проблема обработки и улучшения качества изоб-
ражений, полученных с гидролокатора бокового обзора (ГБО) АНПА. Известно,
что гидроакустический канал является весьма специфическим вследствие нестаци-
онарности рефракционных и иных физических эффектов, что проявляется в виде
многолучевости, интерференции и может приводить не только к сильным искажени-
ям получаемого изображения, но и к его полной потере. Изображение, полученное
ГБО, имеет множество дефектов в виде импульсных шумов и низкоамплитудных
помех (белого шума). В работах [1,2] предложен метод двойной фильтрации улуч-
шения качества гидроакустических изображений, полученных с ГБО АНПА. Ал-
горитм основывается на теории интерполяции функций с финитным спектром [3].
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
216
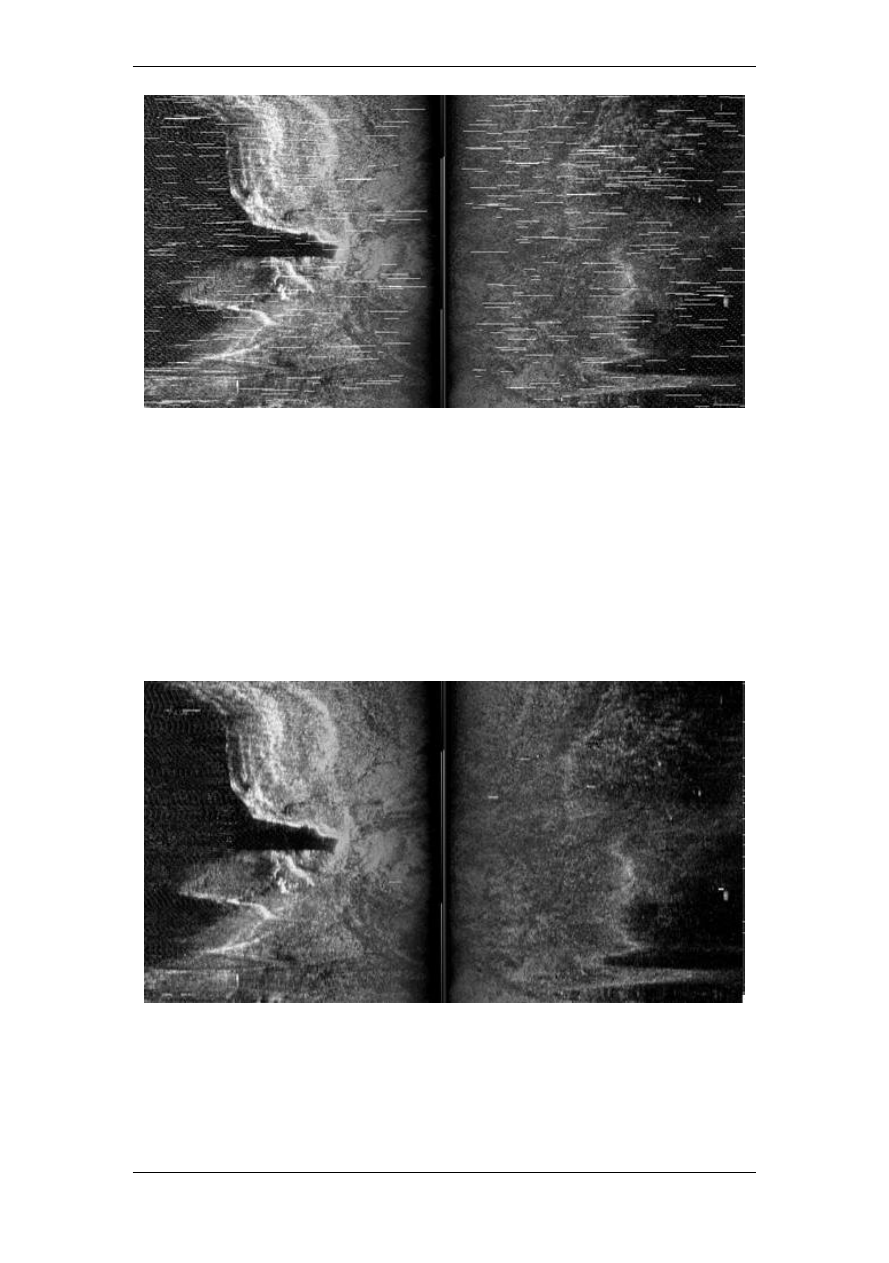
Рис. 1.
Пример гидроакустического изображения
Применение интерполяционных формул для функций с финитным спектром оправ-
дано для решения задачи восстановления гидроакустических изображений, так как
спектр сигнала от ГБО сосредоточен в ограниченном диапазоне частот. Проведен-
ные численные эксперименты с реальными данными [1,2] на основе метода двойной
фильтрации продемонстрировали заметное улучшение качества гидроакустических
изображений по сравнению с традиционным медианным методом. На рисунке 1 пред-
ставлен пример гидроэхолокационного изображения морского дна с дополнитель-
ным импульсным шумом. На рисунке 2 – результат его обработки на основе метода
двойной фильтрации. Как правило, обработка данных, полученных с АНПА, осу-
Рис. 2.
Обработка изображения методом двойной фильтрации
ществляется в лабораторных условиях. В среднем изображения, полученные ГБО,
занимают от 100 до 200 Мбайт и нередко доходит до 1 Гбайт. Время, затрачиваемое
на обработку изображения с помощью метода двойной фильтрации, значительно
превышает время обработки, осуществляемой медианным методом. В связи с этим
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
217
актуальным является программная реализация метода двойной фильтрации на ос-
нове параллельного вычислительного алгоритма. Восстанавливаемый объект - это
изображение, которое для удобства использования средствами программы перево-
диться в двумерный массив. Далее каждый столбец массива проходит специальную
обработку (непосредственно метод двойной фильтрации) и записывается в выходной
файл-изображение. Для данного метода существует несколько подходов перевода
последовательного алгоритма в параллельный. 1-ый способ: передача главным про-
цессором одного столбца из массива для обработки методом двойной фильтрации n
дочерними процессорами. Модель первого способа изображена на рисунке 3. Время
Рис. 3.
Модель 1-го способа
на обработку изображения разным числом процессоров изображено на рисунке 4.
Из рисунка 4 видно, что уменьшение времени при увеличении числа процессоров
Рис. 4.
График зависимости времени обработки изображения (мс) от числа процессоров
происходит только до
n
= 16
узлов. Дальнейшее увеличение числа процессоров
приводит к увеличению времени. Таким образом, при использовании более 16 про-
цессоров для 1-го способа перевода последовательного алгоритма в параллельный
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
218
эффективность утрачивается. При выполнении алгоритма больше времени тратить-
ся на передачу данных от главного процесса дочерним и обратно, чем на выполнение
метода двойной фильтрации каждым дочерним процессором. На основе полученных
результатов необходимо предложить другой вариант решения проблемы. Для этого
можно обобщить 1-ый способ. 2-ой способ: передача главным процессором группы
из
m
столбцов массива для обработки методом двойной фильтрации
n
дочерними
процессорами. Модель второго способа представлена на рисунке 5. Для использова-
Рис. 5.
Модель 2-го способа
ния 2-го способа перевода последовательного алгоритма в параллельный необходимо
установить зависимость между числом процессоров, числом передаваемых каждому
процессору столбцов и временем выполнения программы. Таким образом, необходи-
мо найти такое число
m
передаваемых столбцов дочернему процессору, при котором
время на пересылку массива данных будет много меньше времени выполнения об-
работки данного массива методом двойной фильтрации. В эксперименте использо-
вались следующие значения: число процессоров
n
=
{
1
,
2
,
4
,
8
,
16
,
32
,
64
,
128
}
, число
блоков
m
=
{
2
,
4
,
8
}
. На графике отмечен рост производительности c увеличением
числа процессоров до 16 узлов для всех
m
. Дальнейшее увеличение числа узлов
дает рост только для
m
=
{
2
,
8
}
. При
n
= 64
наблюдается увеличение времени вы-
полнения алгоритма в сравнении со значением при
n
= 32
. Минимальное значение
времени
t
выполнения алгоритма при
n
= 128
, m
= 2 :
t
= 24320
.
Тем не менее,
при
n
= 16
, m
= 2 :
t
= 24790
. Следовательно, эксперимент с меньшим числом про-
цессоров показал схожий результат c экспериментом, выполненном на 128 процессо-
рах. Таким образом, оптимальное число процессоров
n
= 16
и оптимальное количе-
ство столбцов изображения для передачи дочерним процессорам
m
= 2
. Авторами
разработан параллельный вычислительный алгоритм, реализующий метод двойной
фильтрации улучшения качества гидроакустических изображений. Осуществлена
программная реализация алгоритма на языке С++ с использованием технологии
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.
219
параллельных вычислений MPI. Проведен анализ зависимости скорости выполне-
ния алгоритма от количества используемых вычислительных ядер. Сделана оценка
эффективности разных способов перевода последовательного алгоритма в парал-
лельный. Численные эксперименты проведены на кластере Дальневосточного феде-
рального университета. Работа выполнена при финансовой поддержке Российского
фонда фундаментальных исследований (код проекта 11-01-98521) и Федеральной
целевой программы "Научные и научно-педагогические кадры инновационной Рос-
сии”, (госконтракты 16.740.11.0456, 14.740.11.1000).
Список литературы
1.
А.Е. Ковтанюк, А.А. Сущенко, И.Б. Агафонов, В.В. Золотарев. Интерполяционные
методы в задаче улучшения качества гидроакустических изображений // Техниче-
ские проблемы освоения мирового океана. Материалы 4-й Всероссийской научно-
технической конференции, 3-7 октября 2011 г., Владивосток. С. 284-288.
2.
А.Е. Ковтанюк, А.А. Сущенко, И.Б. Агафонов, В.В. Золотарев. Улучшение качества
гидроакустических изображений методом двойной фильтрации // Подводные иссле-
дования и робототехника. №2(12). 2011. С. 31-37
3.
Алексеев Г.В. Обратные задачи излучения волн и теории сигналов. Владивосток: Изд-
во ДВГУ, 1991.
Сборник материалов XXXVII Дальневосточной Математической Школы-Семинара
имени академика Е.В. Золотова, Владивосток, 8 – 14 сентября 2013 г.