Файл: белорусский государственный технологический университет.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.10.2023
Просмотров: 58
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
= 2∙515 + 70 = 1100 МПа.
σHlimb2 = 2∙490 + 70 = 1050 МПа.
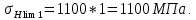
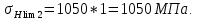
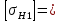
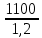 *0,9 = 825 МПа.
*0,9 = 825 МПа.
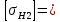
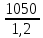 *0,9 = 787,5 МПа.
*0,9 = 787,5 МПа.
В качестве допускаемого контактного напряжения принимаем:
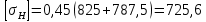 МПа –для косозубого зацепления.
МПа –для косозубого зацепления.
 Допускаемые напряжения на выносливость зубьев при изгибе определяем по формуле:
Допускаемые напряжения на выносливость зубьев при изгибе определяем по формуле:
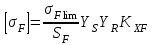 (3.3)
(3.3)
где YS– коэффициент, учитывающий градиент напряжения и чувствительности материала и концентрации напряжений ( YS= 1);
YR – коэффициент, учитывающий шероховатость переходной поверхности(YR = 1);
KXF– коэффициент, учитывающий размеры зубчатого колеса (KXF = 1);
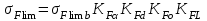 (3.4)
(3.4)
где σFlimb– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений:
σFlimb = 1,8НВ = 945 МПа – шестерня,
σFlimb= 1,8НВ = 900 МПа – колесо;
KFα – коэффициент, учитывающий влияние шлифования переходной поверхности зуба (KFα = 0,9);
KFd– коэффициент, учитывающий деформационное упрочнение или электрохимическую обработку переходной поверхности (KFβ = 1);
KFO– коэффициент, учитывающий влияние двухстороннего приложения нагрузки (KFO= 1);
KF1 – коэффициент долговечности (KF1=1);
SF– коэффициент безопасности;
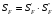 (3.5)
(3.5)
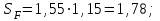
Тогда для зубьев шестерни
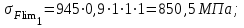
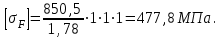
Для зубьев колеса
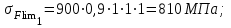
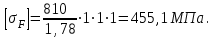
Выполним проектировочный расчет, который служит для предварительного определения размеров. При расчетах зубчатой передачи принимаем, что индекс «1» относится к шестерне, а индекс «2» – к колесу. Поэтому значение крутящего момента Т1 соответствует валу, на котором установлена шестерня.
При проектировочном расчете ориентировочно определяем начальный диаметр шестерни (мм) по формуле:
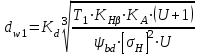 , (3.6)
, (3.6)
 где
где 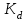 – вспомогательный коэффициент, 675 МПа для косозубых колес;
– вспомогательный коэффициент, 675 МПа для косозубых колес;
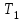 – крутящий момент на ведущем валу, Н·м;
– крутящий момент на ведущем валу, Н·м;
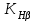 = 1,16 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, зависящий от твердости материала колес НВ, кинематической схемы передачи и величины ψbd; определяется по номограммам (рис. 3.2.) [1];
= 1,16 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, зависящий от твердости материала колес НВ, кинематической схемы передачи и величины ψbd; определяется по номограммам (рис. 3.2.) [1];
KA = 1,25 – коэффициент внешней динамической нагрузки (табл.3.3.);
U= 4,5 – передаточное число рассчитываемой зубчатой пары (принимается из кинематического расчета);
ψbd = 0,7 – коэффициент ширины зубчатого венца (задан);
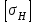 – допускаемые контактные напряжения (определены ранее).
– допускаемые контактные напряжения (определены ранее).
Тогда получим
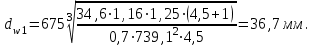
Начальный диаметр колеса:
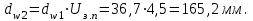 .
.
Ориентировочное значение межосевого расстояния при внешнем зацеплении
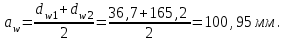
Нормальный модуль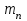 для косозубых колес принимаем в зависимости от межосевого расстояния:
для косозубых колес принимаем в зависимости от межосевого расстояния:
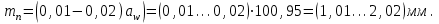
Полученое значения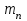
округляем до ближайшего стандартных значений по ГОСТ 9563 (табл.3.5) [1].
Принимаем mn = 1,5 мм.
Предварительно принимается угол наклона линии зубьев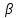 равный 130.
равный 130.
Определяем число зубьев косозубой шестерни
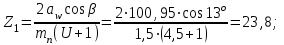
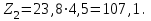 .
.
Значения Z1 и Z2 округляют до целых чисел. Принимаем Z1 = 24, Z2 = 107.
Уточняется передаточное число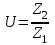 , отклонение от требуемого значения не должно превышать 5 %.
, отклонение от требуемого значения не должно превышать 5 %.
U = Z2/Z1 = 107/24 = 4,46.
Отклонение составляет 0,9% < 5%.

Угол наклона линии зубьев β уточняется по формуле
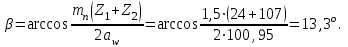
Уточняем диаметр начальной окружности шестерни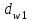 и колеса
и колеса 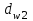

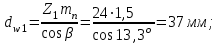
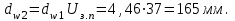
Уточняем межосевое расстояние

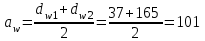 мм.
мм.
Определяется рабочая ширина венца шестерни и колеса
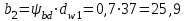 мм;
мм;
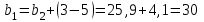 мм.
мм.
Принимаем b1 = 30 мм, b2 = 26 мм.
Определим окружную скорость
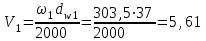 м/с,
м/с,
где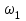 - угловая скорость на валу шестерни, с-1; определяется из кинематического расчета.
- угловая скорость на валу шестерни, с-1; определяется из кинематического расчета.
Определяем степень точности передачи в зависимости от окружной скорости, условий ее работы и возможности производства в соответствии с табл. 3.6 [1]. Принимаем 8-ю степень точности.
Выполним проверочный расчет закрытой зубчатой
передачи на контактную выносливость.
Расчетные контактные напряжения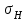
, МПа в полюсе зацепления определяют по формуле:
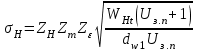
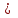
 , (3.7)
, (3.7)
где ZH – коэффициент, учитывающий форму сопряженных поверхностей зубьев, принимается равным 1,73 при = 13,3о;
= 13,3о;
Zm – коэффициент, учитывающий механические свойства материала сопряженных зубчатых колес, принимается равным 275;
Zε – коэффициент, учитывающий суммарную длину контактных линий, Zε = 0,8 для косозубых;
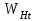 – удельная расчетная окружная сила, Н/мм
– удельная расчетная окружная сила, Н/мм
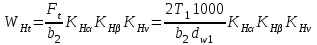 ,
,
где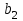 – ширина колеса, мм;
– ширина колеса, мм;
 – делительный диаметр шестерни, мм;
– делительный диаметр шестерни, мм;

 – крутящий момент на валу шестерни, Н·м;
– крутящий момент на валу шестерни, Н·м;
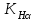 – коэффициент, учитывающий распределение нагрузки между зубьями; для косозубых колес при степени точности 8 –
– коэффициент, учитывающий распределение нагрузки между зубьями; для косозубых колес при степени точности 8 –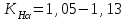 (
(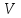 < 10 м/с);
< 10 м/с);
 - определяется по рис. 3.2 [1];
- определяется по рис. 3.2 [1];
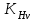 - коэффициент, учитывающий динамическую нагрузку в зацеплении, определяется по табл.3.7 [1].
- коэффициент, учитывающий динамическую нагрузку в зацеплении, определяется по табл.3.7 [1].
Тогда
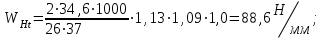
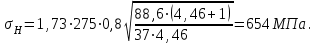
Полученное значение должно удовлетворять условию
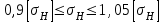 ,
,
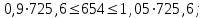
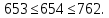
Условие выполняется.
Выполним проверочный расчет зубьев на выносливость при изгибе.
Расчетные напряжения изгиба зубьев (МПа) определяем по формуле
(МПа) определяем по формуле
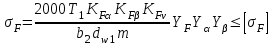 , (3.8)
, (3.8)
где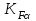 – коэффициент, учитывающий распределение нагрузки между зубьями. Предполагая, что в зацеплении находится одна пара зубьев принимают
– коэффициент, учитывающий распределение нагрузки между зубьями. Предполагая, что в зацеплении находится одна пара зубьев принимают 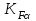 = 1;
= 1;
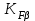 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. Принимается по номограммам в зависимости от твердости материала колес, величина
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. Принимается по номограммам в зависимости от твердости материала колес, величина 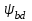 и кинематической схемы передачи (рис. 3.2.) [1],
и кинематической схемы передачи (рис. 3.2.) [1], 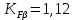 ;
;
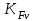 – коэффициент, учитывающий динамическую нагрузку в зацеплении. Определяется по табл. 3.7 [1], KFv = 1,2;
– коэффициент, учитывающий динамическую нагрузку в зацеплении. Определяется по табл. 3.7 [1], KFv = 1,2;
YF – коэффициент, учитывающий форму зуба; определяем по графику (рис. 3.3 [1]) в зависимости от эквивалентного числа зубьев ZV:
ZV =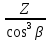 ;
;

 YF = 3,72 для колеса,YF = 3,96 для шестерни;
YF = 3,72 для колеса,YF = 3,96 для шестерни;
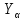 – коэффициент, учитывающий перекрытие зубьев (
– коэффициент, учитывающий перекрытие зубьев ( 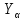 = 1 );
= 1 );
Yβ– коэффициент, учитывающий наклон зуба
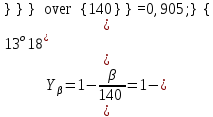
Проверочный расчет зубчатой передачи на выносливость при изгибе производим для менее прочного звена: шестерни или колеса. Для этого необходимо определить отношение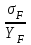 для шестерни и колеса и проверку на выносливость производить для того звена, у которого это отношение меньше.
для шестерни и колеса и проверку на выносливость производить для того звена, у которого это отношение меньше.
Шестерня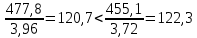 колесо.
колесо.
Проверку на выносливость проводим для шестерни
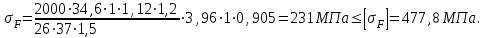
Условие прочности выполняется.
σHlimb2 = 2∙490 + 70 = 1050 МПа.
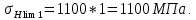
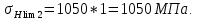
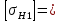
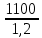 *0,9 = 825 МПа.
*0,9 = 825 МПа.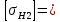
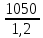 *0,9 = 787,5 МПа.
*0,9 = 787,5 МПа.В качестве допускаемого контактного напряжения принимаем:
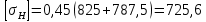 МПа –для косозубого зацепления.
МПа –для косозубого зацепления. Допускаемые напряжения на выносливость зубьев при изгибе определяем по формуле:
Допускаемые напряжения на выносливость зубьев при изгибе определяем по формуле: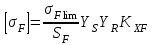 (3.3)
(3.3)где YS– коэффициент, учитывающий градиент напряжения и чувствительности материала и концентрации напряжений ( YS= 1);
YR – коэффициент, учитывающий шероховатость переходной поверхности(YR = 1);
KXF– коэффициент, учитывающий размеры зубчатого колеса (KXF = 1);
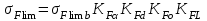 (3.4)
(3.4)где σFlimb– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений:
σFlimb = 1,8НВ = 945 МПа – шестерня,
σFlimb= 1,8НВ = 900 МПа – колесо;
KFα – коэффициент, учитывающий влияние шлифования переходной поверхности зуба (KFα = 0,9);
KFd– коэффициент, учитывающий деформационное упрочнение или электрохимическую обработку переходной поверхности (KFβ = 1);
KFO– коэффициент, учитывающий влияние двухстороннего приложения нагрузки (KFO= 1);
KF1 – коэффициент долговечности (KF1=1);
SF– коэффициент безопасности;
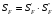 (3.5)
(3.5)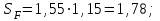
Тогда для зубьев шестерни
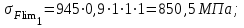
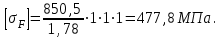
Для зубьев колеса
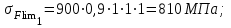
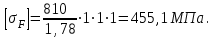
Выполним проектировочный расчет, который служит для предварительного определения размеров. При расчетах зубчатой передачи принимаем, что индекс «1» относится к шестерне, а индекс «2» – к колесу. Поэтому значение крутящего момента Т1 соответствует валу, на котором установлена шестерня.
При проектировочном расчете ориентировочно определяем начальный диаметр шестерни (мм) по формуле:
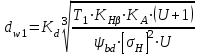 , (3.6)
, (3.6) где
где 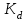 – вспомогательный коэффициент, 675 МПа для косозубых колес;
– вспомогательный коэффициент, 675 МПа для косозубых колес;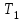 – крутящий момент на ведущем валу, Н·м;
– крутящий момент на ведущем валу, Н·м;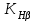 = 1,16 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, зависящий от твердости материала колес НВ, кинематической схемы передачи и величины ψbd; определяется по номограммам (рис. 3.2.) [1];
= 1,16 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца, зависящий от твердости материала колес НВ, кинематической схемы передачи и величины ψbd; определяется по номограммам (рис. 3.2.) [1]; KA = 1,25 – коэффициент внешней динамической нагрузки (табл.3.3.);
U= 4,5 – передаточное число рассчитываемой зубчатой пары (принимается из кинематического расчета);
ψbd = 0,7 – коэффициент ширины зубчатого венца (задан);
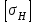 – допускаемые контактные напряжения (определены ранее).
– допускаемые контактные напряжения (определены ранее).Тогда получим
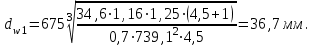
Начальный диаметр колеса:
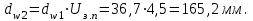 .
.Ориентировочное значение межосевого расстояния при внешнем зацеплении
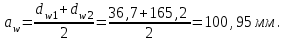
Нормальный модуль
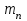 для косозубых колес принимаем в зависимости от межосевого расстояния:
для косозубых колес принимаем в зависимости от межосевого расстояния: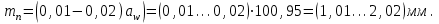
Полученое значения
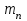
округляем до ближайшего стандартных значений по ГОСТ 9563 (табл.3.5) [1].
Принимаем mn = 1,5 мм.
Предварительно принимается угол наклона линии зубьев
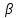 равный 130.
равный 130.Определяем число зубьев косозубой шестерни
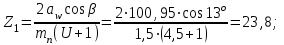
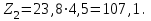 .
.Значения Z1 и Z2 округляют до целых чисел. Принимаем Z1 = 24, Z2 = 107.
Уточняется передаточное число
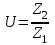 , отклонение от требуемого значения не должно превышать 5 %.
, отклонение от требуемого значения не должно превышать 5 %.U = Z2/Z1 = 107/24 = 4,46.
Отклонение составляет 0,9% < 5%.

Угол наклона линии зубьев β уточняется по формуле
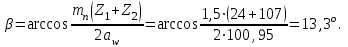
Уточняем диаметр начальной окружности шестерни
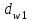 и колеса
и колеса 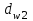

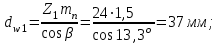
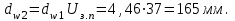
Уточняем межосевое расстояние

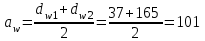 мм.
мм.Определяется рабочая ширина венца шестерни и колеса
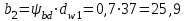 мм;
мм;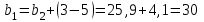 мм.
мм.Принимаем b1 = 30 мм, b2 = 26 мм.
Определим окружную скорость
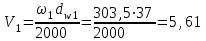 м/с,
м/с,где
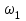 - угловая скорость на валу шестерни, с-1; определяется из кинематического расчета.
- угловая скорость на валу шестерни, с-1; определяется из кинематического расчета.Определяем степень точности передачи в зависимости от окружной скорости, условий ее работы и возможности производства в соответствии с табл. 3.6 [1]. Принимаем 8-ю степень точности.
Выполним проверочный расчет закрытой зубчатой
передачи на контактную выносливость.
Расчетные контактные напряжения
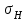
, МПа в полюсе зацепления определяют по формуле:
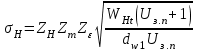
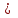
 , (3.7)
, (3.7)где ZH – коэффициент, учитывающий форму сопряженных поверхностей зубьев, принимается равным 1,73 при
 = 13,3о;
= 13,3о; Zm – коэффициент, учитывающий механические свойства материала сопряженных зубчатых колес, принимается равным 275;
Zε – коэффициент, учитывающий суммарную длину контактных линий, Zε = 0,8 для косозубых;
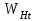 – удельная расчетная окружная сила, Н/мм
– удельная расчетная окружная сила, Н/мм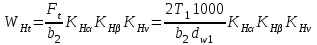 ,
,где
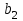 – ширина колеса, мм;
– ширина колеса, мм; – делительный диаметр шестерни, мм;
– делительный диаметр шестерни, мм;
 – крутящий момент на валу шестерни, Н·м;
– крутящий момент на валу шестерни, Н·м;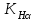 – коэффициент, учитывающий распределение нагрузки между зубьями; для косозубых колес при степени точности 8 –
– коэффициент, учитывающий распределение нагрузки между зубьями; для косозубых колес при степени точности 8 –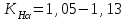 (
(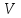 < 10 м/с);
< 10 м/с); - определяется по рис. 3.2 [1];
- определяется по рис. 3.2 [1];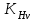 - коэффициент, учитывающий динамическую нагрузку в зацеплении, определяется по табл.3.7 [1].
- коэффициент, учитывающий динамическую нагрузку в зацеплении, определяется по табл.3.7 [1].Тогда
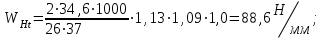
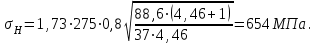
Полученное значение должно удовлетворять условию
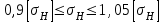 ,
,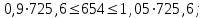
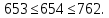
Условие выполняется.
Выполним проверочный расчет зубьев на выносливость при изгибе.
Расчетные напряжения изгиба зубьев
 (МПа) определяем по формуле
(МПа) определяем по формуле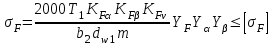 , (3.8)
, (3.8)где
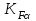 – коэффициент, учитывающий распределение нагрузки между зубьями. Предполагая, что в зацеплении находится одна пара зубьев принимают
– коэффициент, учитывающий распределение нагрузки между зубьями. Предполагая, что в зацеплении находится одна пара зубьев принимают 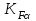 = 1;
= 1;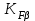 – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. Принимается по номограммам в зависимости от твердости материала колес, величина
– коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца. Принимается по номограммам в зависимости от твердости материала колес, величина 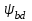 и кинематической схемы передачи (рис. 3.2.) [1],
и кинематической схемы передачи (рис. 3.2.) [1], 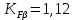 ;
;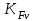 – коэффициент, учитывающий динамическую нагрузку в зацеплении. Определяется по табл. 3.7 [1], KFv = 1,2;
– коэффициент, учитывающий динамическую нагрузку в зацеплении. Определяется по табл. 3.7 [1], KFv = 1,2;YF – коэффициент, учитывающий форму зуба; определяем по графику (рис. 3.3 [1]) в зависимости от эквивалентного числа зубьев ZV:
ZV =
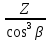 ;
;
 YF = 3,72 для колеса,YF = 3,96 для шестерни;
YF = 3,72 для колеса,YF = 3,96 для шестерни;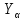 – коэффициент, учитывающий перекрытие зубьев (
– коэффициент, учитывающий перекрытие зубьев ( 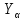 = 1 );
= 1 );Yβ– коэффициент, учитывающий наклон зуба
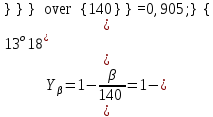
Проверочный расчет зубчатой передачи на выносливость при изгибе производим для менее прочного звена: шестерни или колеса. Для этого необходимо определить отношение
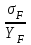 для шестерни и колеса и проверку на выносливость производить для того звена, у которого это отношение меньше.
для шестерни и колеса и проверку на выносливость производить для того звена, у которого это отношение меньше.Шестерня
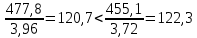 колесо.
колесо.Проверку на выносливость проводим для шестерни
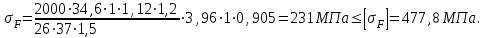
Условие прочности выполняется.