Файл: белорусский государственный технологический университет.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 29.10.2023

Просмотров: 62

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Определим силы, действующие в зацеплении цилиндрической передачи.

На рисунке 3.1 представлена схема сил, действующих в косозубом зацеплении.



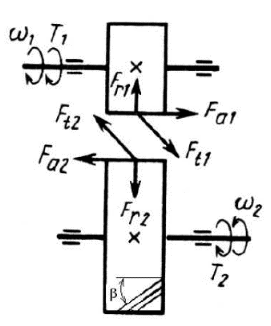
Рисунок 3.1 - Силы в цилиндрическом косозубом зацеплении

Окружная сила

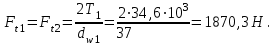. (3.9)

Радиальная сила

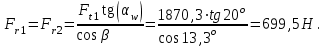. (3.10)

Осевая сила

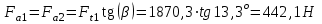, (3.11)

где Т1 – крутящий момент на ведущем валу, Н·м;

– диаметр начальной начальной окружности, мм;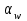

– угол зацепления (стандартный 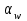= 20о);

– угол наклона линии зуба.

Значения Т и 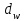брались для вала шестерни.

Расчет размеров колес цилиндрической передачи.

По рекомендациям [1] зубчатое колесо изготовляем кованным.

На рисунке 3.2 представлена конструкция цилиндрического колеса.

Определим основные параметры цилиндрического зубчатого колеса по таблице 8.1 [1].

Высота головки зуба:

ha = mn = 1,5 мм. (3.12)

Высота ножки зуба:

hf = 1,25·mn , (3.13)

hf = 1,25·1,5 = 1,875 мм.

Высота зуба:

h = ha + hf , (3.14)

h = 1,5 + 1,875 = 3,375 мм.

Диаметр окружности вершин зубьев:

dа = dw + 2·ha , (3.15)

dа1 = 37 + 2·1,5 = 40 мм;

dа2 = 165 + 2·1,5 = 168 мм;

Диаметр окружности впадин зубьев

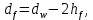(3.16)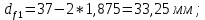









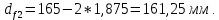
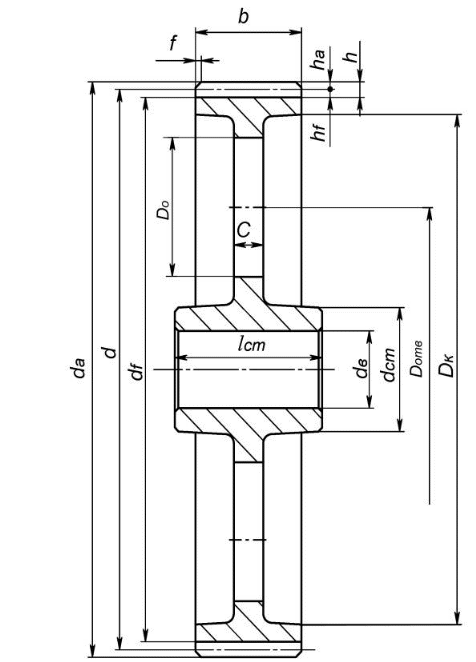
Рисунок 3.2 - Элементы цилиндрического зубчатого колеса

Толщина обода:

а = (2,0…4,0)·ha , (3.17)

a =

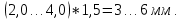
Принимаем а = 6 мм.

Внутренний диаметр обода:

Dk2 = df2 - 2·a, (3.18)

Dk2 = 161,25 – 2*6 = 149,25 мм.

Толщина диска:

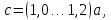(3.19)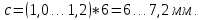



Принимаем с = 7 мм.

Фаска на торце зуба:

f = (0,6…0,7)·ha , (3.20)



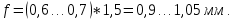
Принимаем f = 1,0 мм.

Диаметр вала под ступицей колеса:

dв = d4 = 48 мм.

Диаметр ступицы:

dст = (1,6…1,8)·dв , (3.21)

dст = (1,6…1,8)*48 = 76,8…86,4 мм.

Принимаем dст = 80 мм.

Длина ступицы:

lст = (1,2…1,6)·dв , (3.22)
lст = (1,2…1,6)·48 = 57,6…76,8 мм.

Принимаем lст = 70 мм.

Диаметр отверстий в диске:

Do = 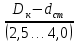, (3.23)

Do = 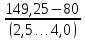= 27,7…17,3 мм.

Принимаем Do = 20 мм.

Диаметр окружности центров отверстий:

Dотв = 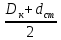, (3.24)

Dотв = 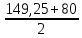= 114,625 мм.

Принимаем Do = 115 мм.

4. Проектный и проверочный расчеты открытых передач

4.1. Проектный расчет конической открытой передачи

По рекомендациям [1] открытые зубчатые передачи рассчитывают только на выносливость зубьев при изгибе, так как абразивное изнашивание поверхностей зубьев открытых передач происходит быстрое, чем усталостное контактное выкрашивание.

По рекомендациям [1] для изготовления зубчатых колес конической передачи используем следующие материалы:

шестерня - сталь 45;

термообработка – улучшение;

твердость 235 HВ;

предел прочности 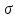в = 780 МПа;

предел текучести 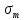= 540 МПа;

колесо - сталь 45;

термообработка – нормализация;

твердость 190 HВ;

предел прочности 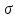в = 600 МПа;

предел текучести 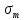= 320 МПа.

Допускаемые напряжения на выносливость зубьев при изгибе определяем по формуле:

(4.1)

где YS– коэффициент, учитывающий градиент напряжения и чувствительности материала и концентрации напряжений ( YS= 1);

YR – коэффициент, учитывающий шероховатость переходной поверхности(YR = 1);

KXF– коэффициент, учитывающий размеры зубчатого колеса (KXF = 1);

(4.2)

где σFlimb– предел выносливости зубьев при изгибе, соответствующий базовому числу циклов перемены напряжений:

σFlimb = 1,8НВ = 1044 МПа­ – шестерня,

σFlimb= 1,8НВ = 882 МПа – ­колесо;

KFα – коэффициент, учитывающий влияние шлифования переходной поверхности зуба (KFα = 1,1);

KFd– коэффициент, учитывающий деформационное упрочнение или электрохимическую обработку переходной поверхности (KFβ = 1);

KFO– коэффициент, учитывающий влияние двухстороннего приложения нагрузки (KFO= 1);

KF1 – коэффициент долговечности (KF1=1);

SF– коэффициент безопасности;

(4.3)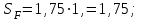



Тогда для зубьев шестерни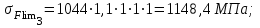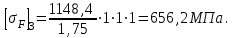





Для зубьев колеса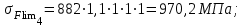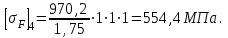




Выполним проектный расчет передачи.

Принимаем Z3 = 15.

Тогда

Z4 = Z3*Uо.п = 15*3,15 = 47,25.

Принимаем Z4 = 47.

Действительное передаточное число

Uо.п= Z4/Z3 = 47/15 = 3,13.

Угол делительного конуса шестерни и колеса (рис. 4.1), град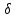

3 = arctg(Z3/Z4) = arctg(15/47) = 17,7o;

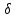4 = arctg(Z4/Z3) = arctg(47/15) = 72,3o.

Эквивалентное число зубьев

ZV3(4)= Z3(4)/cosδ3(4).

ZV3 =

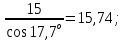
ZV4 =

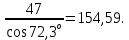
Расчетный средний модуль зацепления определяется по усталостному напряжению изгиба зуба по формуле:

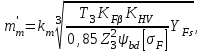(4.4)

где km= 14;

ψbd – коэффициент ширины зубчатого венца шестерни относительно ее диаметра ψbd = 0,3 (задан);

KFβ – коэффициент, учитывающий неравномерность распределения нагрузки по ширине венца ;

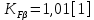KHV – коэффициент внешней динамической нагрузки 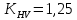[1].

YF – коэффициент, учитывающий форму зуба, (рис.3.3 [1]).




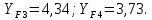
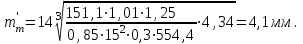
Расчет производим для элемента пары «шестерня-колесо», у которого меньшая величина отношения [σF3(4)]/YF3(4).

Для шестерни -

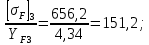
Для колеса -

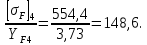
Следовательно, расчет проводим для колеса.

Ширина венца

b= ψbdm′mz3 = 0,3*4,1*15 = 18,45 мм;

Принимаем b = 20 мм.

Внешнее конусное расстояние

R′e= 0,5(m′mZ3/sinδ′4+b) = 0,5(4,1*15/sin 17,7o + 20) = 111,14 мм; (b/R′e≤0,3), 20/111,14 = 0,180. Условие выполняется



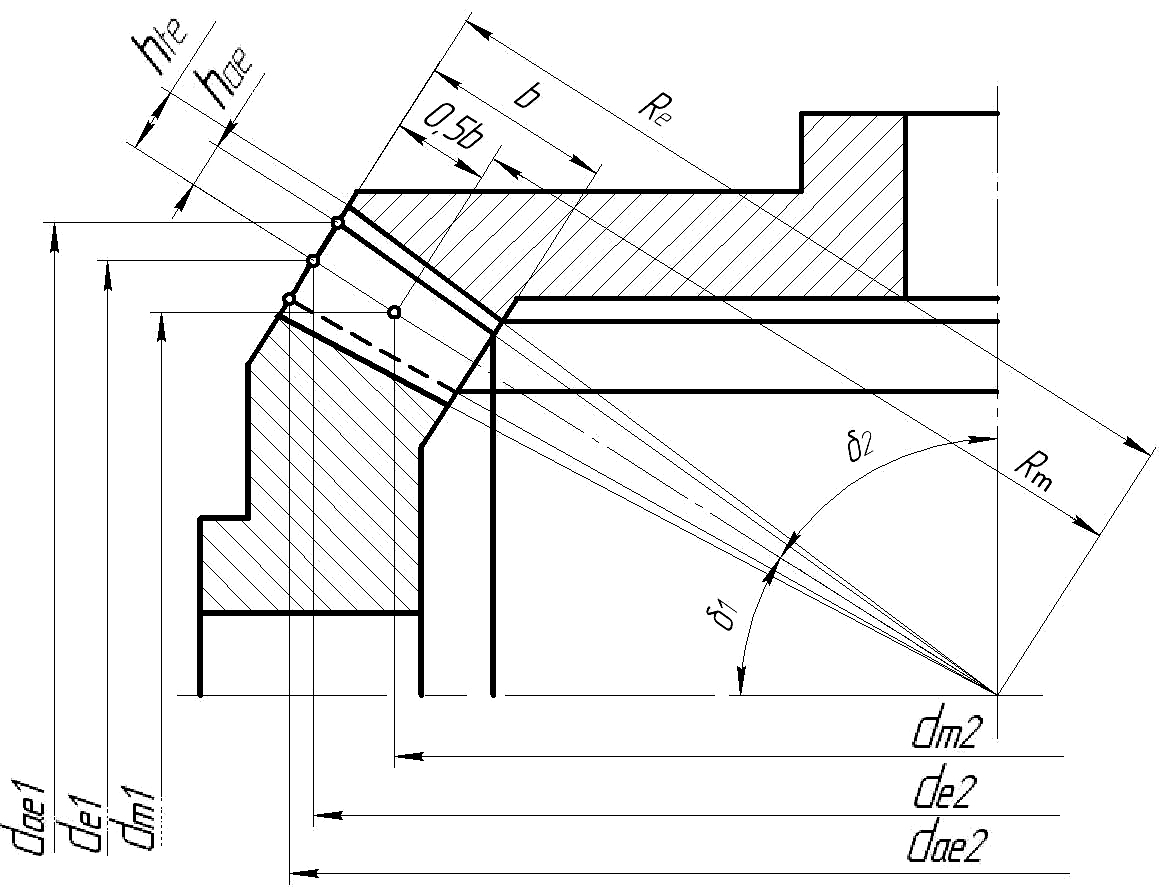
Рис. 4.1. Основные параметры конической передачи




Наружный модуль, мм

m′te = m′m R′e /(R′e - 0,5b) = 4,1*111,14/(111,14 – 0,5*20) = 4,5 мм.

m′teокругляют до ближайшего стандартного значения mte= mn, мм (табл. 3.5[1]).

Принимаем

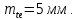
Действительное внешнее конусное расстояние, мм

Re= 0,5mte 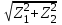= 0,5*5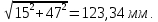

Средний модуль зацепления, мм

mm = mte(Re - 0,5b)/Re = 5(123,34 – 0,5*20)/123,34 = 4,59 мм.

Средний делительный диаметр

шестерни

dm3 =mmZ3 = 4,59*15 = 68,92 мм;

колеса

dm4 =mmZ4 = 4,59*47 = 215,73 мм.


Выполним проверочный расчет по усталостному напряжению изгиба зуба.
Расчетные напряжения изгиба (МПа) должны удовлетворять зависимости

σF4 = YF4WFt/(0,85mm) ≤ [σF4].

Окружная скорость колес, м/с

V4= π dm4n4/(60·103) = 3,14*215,73*204/(60*103) = 2,3 м/с.

Степень точности - 8 (табл. 3.6) [1].

Удельная окружная динамическая сила, Н/мм

WFV= δFg0V4

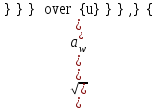
где δF = 0,11 – коэффициент, учитывающий влияние вида зубчатой передачи и модификации профиля зуба на динамическую нагрузку (табл. 4.2) [1];

g0 = 5,3 – коэффициент, учитывающий влияние разности шагов зацепления зубьев шестерни и колеса (табл. 4.3) [1];

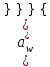=0,5(dm3+dm4) = 0,5(68,92 + 215,73) = 142,33 мм – условное межосевое расстояние, определяющее моменты инерции колес.

Тогда

WFV= 0,16*5,3*2,3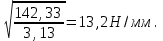

Удельная расчетная окружная сила в зоне ее наибольшей концентрации
, Н/мм

WFtp= Ft4 KFβ/b= 3434*1,01/20 = 173,4 H/мм,

где Ft3(4) – окружная сила в зацеплении:



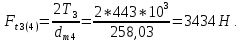
Коэффициент, учитывающий динамическую нагрузку в зацеплении,

KFv= 1 + (WFv/WFtp) = 1 + (13,2/173,2) = 1,08.

Удельная расчетная окружная сила при изгибе, Н/мм

WFt= Ft KFβKFvKА/b= 3434*1,01*1,08*1,0/20 = 187,3 H/мм.

Тогда

;

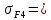
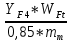
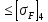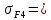
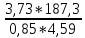= 179,1 МПа ;

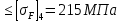Условие прочности зубьев на изгиб выполняется.
Определим силы в зацеплении (рис. 4.2).



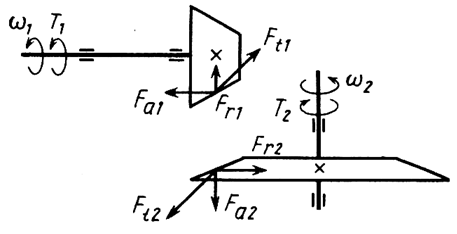
Рис. 4.2. Силы в зацеплении конических передач

Усилия в зацеплении прямозубых конических колес (рис. 4.2):

Окружные силы, Н

; .

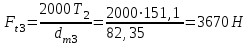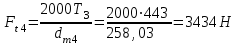Радиальные силы, Н

;



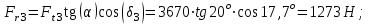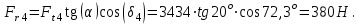
Осевые силы, Н:

;



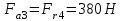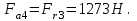
Здесь α = 20˚.

Расчет размеров колес конической передачи

На рисунке 4.3 изображена конструкция конического колеса.



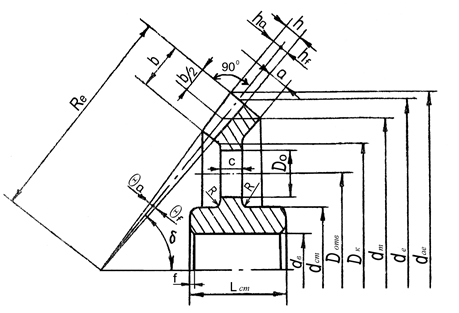
Рис. 4.3. Конструкция и основные геометрические параметры конического колеса

Угол делительного конуса шестерни δ3,

3 = arctg(Z3/Z4) = arctg(15/47) = 17,7o;

Угол делительного конуса колеса δ2

Смотрите также файлы