Файл: Математической физики.doc

Задачи

Постановка начально-краевых задач

В задачах 1 − 13 описаны некоторые физические процессы. Следует выбрать функцию, характеризующую указанный процесс, вывести для нее дифференциальное уравнение, сформулировать для этой функции начальные и граничные условия. Все необходимые параметры системы предполагаются известными.

1. Сформулировать задачу о продольных колебаниях однородного упругого стержня постоянного сечения S длины l при произвольных начальных отклонении и скорости. Рассмотреть следующие случаи:

а) к концам нерастянутого стержня и , начиная с момента приложены силы и , действующие вдоль стержня;

б) концы стержня закреплены упруго, т.е. на них действуют силы, пропорциональные их отклонению;

в) конец стержня испытывает сопротивление, пропорциональное скорости, а конец закреплен жестко;

г) конец стержня закреплен, а конец свободен и к нему прикреплена точечная масса m;

д) стержень закреплен на конце и растянут силой F, приложенной к другому концу; в момент действие силы внезапно прекращается;

е) стержень (на единицу длины) испытывает действие пропорциональной скорости силы сопротивления отклонению, а концы стержня двигаются по заданным законам и

---

;

ж) начиная с момента , стержень испытывает действие направленной вдоль оси x силы объемной плотности , а концы стержня свободны. (Такую силу можно создать, например, с помощью магнитного поля.)

2. Начиная с момента , один конец прямолинейного упругого однородного стержня совершает продольные колебания по заданному закону, а к другому концу приложена сила , направленная по оси стержня. В момент стержень был неподвижен и находился в равновесном положении. Поставить задачу для определения его малых продольных колебаний.

3. Сформулировать задачу о продольных колебаниях однородного упругого стержня переменного сечения длины l при произвольных начальных отклонении и скорости для случая, когда стержень имеет форму усеченного конуса с радиусами оснований r и R , причем основания закреплены жестко.

4. Сформулировать задачу о продольных колебаниях однородного упругого стержня переменного сечения длины l при произвольных начальных отклонении и скорости для случая, когда конец стержня закреплен упруго, а к концу , начиная с момента , приложена продольная сила на единицу площади сечения.

5. Поставить задачу о малых поперечных колебаниях струны в среде с сопротивлением, пропорциональным скорости, предполагая, что

а) концы струны закреплены жестко;

б) один конец свободен, а на другой действует переменная поперечная сила

---

.

6. Однородная струна с закрепленными концами находится во внешнем поперечном магнитном поле с индукцией B. Поставить задачу о колебаниях этой струны, если по ней течет переменный ток I(t).

7. Поставить задачу о продольных колебаниях однородного упругого вертикального стержня, пренебрегая действием силы тяжести на частицы стержня, если верхний конец стержня закреплен жестко, а к нижнему концу прикреплен груз массой M, причем за начальное состояние принимается ненапряженное состояние стержня (т.е. в начальный момент времени из-под груза убирается подставка и он начинает растягивать стержень).

8. Верхний конец упругого однородного вертикально подвешенного тяжелого стержня жестко прикреплен к потолку свободно падающего лифта, который, достигнув скорости v, мгновенно останавливается. Поставить задачу о продольных колебаниях этого стержня.

9. Поставить задачу о поперечных колебаниях тяжелой однородной струны относительно вертикального положения равновесия, если ее верхний конец жестко закреплен, а нижний свободен.

10. Неоднородная струна линейной плотности совершает поперечные колебания около горизонтального положения в поле силы тяжести. В точках струны укреплены шарики массами . Описать движение струны при произвольных начальных условиях для случаев:

а) левый конец струны свободен, правый движется по закону ;

б) левый конец струны закреплен, к правому приложена сила .

11. Однородная струна при вращении вокруг вертикальной оси с постоянной угловой скоростью находится в горизонтальной плоскости, причем один конец струны прикреплен к некоторой точке оси, а другой свободен. В момент

---

точкам струны сообщают малые вертикальные отклонения и скорости. Поставить задачу для определения отклонений точек струны от плоскости равновесного движения. Силой тяжести пренебречь.

12. Два полуограниченных упругих однородных стержня с одинаковыми поперечными сечениями S соединены торцами и составляют один неограниченный стержень. Пусть и - плотность и модуль упругости одного из них, а и - другого. Поставить задачу для определения отклонений сечений стержня от их положения покоя, если заданы их начальные отклонения и скорости.

13. Решить предыдущую задачу, считая, что между торцами составляющих стержней закреплена жесткая прокладка пренебрежимо малой толщины с массой m.

---

Решение задач о свободных колебаниях струны методом Даламбера и методом отражений

В
задачах 14 − 19 указаны начальные возмущения струны при . Решить задачи о свободных колебаниях струны графически; изобразить форму струны в моменты времени , где ; найти формулы, описывающие профиль струны в эти моменты.

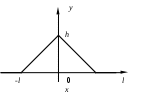
14. Бесконечная струна возбуждена локальным отклонением, изображенным на рис.11 (оттянута за одну из своих точек), и отпущена без начальной скорости.
Рис. 11

15. Бесконечной невозмущенной струне сообщена на отрезке поперечная начальная скорость ; вне этого отрезка начальная скорость равна нулю.

16. Полубесконечная струна, закрепленная на конце , возбуждена начальным отклонением, изображенным на рис.12. Начальные скорости струны равны нулю.

Решить эту задачу для случая, когда конец свободен.


Рис.12
17. Полубесконечной невозмущенной струне в начальный момент с помощью поперечного удара передается импульс I в малой окрестности точки x₀. Рассмотреть случаи, когда конец закреплен или свободен.

18. В начальный момент времени струна длины l с закрепленными концами была оттянута за одну из своих внутренних точек x₀ и отпущена без начальной скорости. Рассмотреть случаи .

19. Концы струны

---