ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 429
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Часть 1
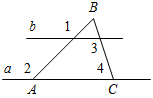
А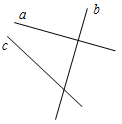 1. На рисунке 1 секущей является прямая…
1. На рисунке 1 секущей является прямая…
а) а; б) с; в) b; г) а или с.
Рис. 1
А2. Для угла 4 накрест лежащим будет угол…
а) 2; б) 5; в) 6; г) 7.
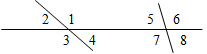
Рис. 2
А3. На рисунке 3 углы 1 и 2 являются…
а) односторонними; в) соответственными;
б) накрест лежащими; г) смежными.
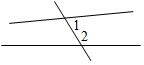
Рис. 3
А4. Дан равносторонний треугольник BCD. Через вершину D провести прямых, параллельных прямой ВС…
а) можно две; в) нельзя ни одной;
б) можно бесконечное множество; г) можно одну.
А5. На рисунке 4 1 = 54°. Прямые а и b будут параллельными, если 2 равен…
а) 54°; б) 54° или 126°; в) 126°; г) 36°.
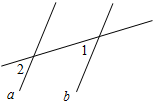
Рис. 4
А6. Прямые будут параллельными на рисунке:
а)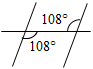 в)
в) 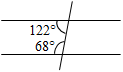
б)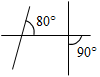 г)
г) 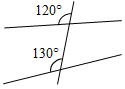
Рис. 5
А7. На рисунке а, b, с пересечены секущей d. Параллельными прямыми будут прямые…
а) а и b; б) b и с; в) а и с; г) а, b и с.
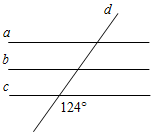
Рис. 6
А8. Верным является высказывание:
а) Если две параллельные прямые пересечены третьей, то сумма накрест лежащих углов равна 180°.
б) Если при пересечении двух прямых секущей накрест лежащие углы в сумме составляют 180°, то прямые параллельны.
в) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
г) Если две прямые параллельны третьей прямой, то они перпендикулярны.
Часть 2
В1. Прямые а и b, изображенные на рисунке
, являются ______________________________________________
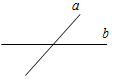
Рис. 7
В2. Из всех углов, изображенных на рисунке, односторонними углами являются углы _____________________
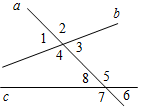
Рис. 8
В3. На рисунке 1 = 135°, 2 = 45°. Тогда прямые т и п будут ________________________________________
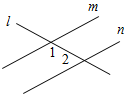
Рис. 9
В4. На рисунке а || b, 3 = 108°. Тогда 1 = ________________________________________________________
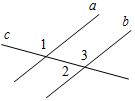
Рис. 10
В5. На рисунке а || b, 1 на 50° меньше 3. Тогда 2 = _______________________________________________
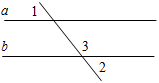
Рис. 11
В6. На рисунке прямые а и b – параллельны, 1 = 80°, 3 = 50°. Тогда 2 = _____________________________
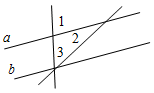
Рис. 12
В7. На рисунке через вершину С треугольника BCD проведена прямая KL, параллельная стороне треугольника BD. При этом BCK = 56°, DCL = 64°. Тогда средним углом треугольника будет угол ______________________
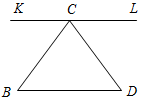
Рис. 13
Часть 3
С1. Отрезок DМ – биссектриса треугольника CDE. Через точку М проведена прямая, пересекающая сторону DE в точке N так, что DN = MN. Вычислите градусные меры углов треугольника DМN, если CDE = 76°.
Ответы:
Часть 1
Часть 2
Часть 3
С1. Возможный вариант оформления решения задачи.
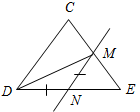
1) DМ – биссектриса треугольника, поэтому CDМ = МDЕ = 38°.
2) DN = MN, поэтому треугольник DNМ является равнобедренным, а значит, МDN = DМN = 38°.
3) Углы DМN и CDМ являются накрест лежащими углами при прямых CD и МN и секущей DМ, а так как внутренние накрест лежащие углы при прямых CD и МN и секущей DМ равны, то прямые DC и МN будут параллельны.
4) Углы CDN и МND являются односторонними при параллельных прямых CD и МN и секущей DЕ, поэтому сумма углов равна 180°. А значит, DNМ = 180° – 76° = 104°.
5) Таким образом, углы треугольника DNМ будут равны 104°, 38°, 38°.
Урок38. Решение задач
Урок39. Контрольная работа № 3
Ресурсный материал
Контрольная работа
В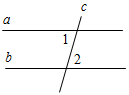 ариант I
ариант I
1. Дано: а || b, с – секущая, 1 + 2 = 102°.
Найти: все образовавшиеся углы.
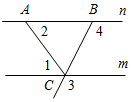
2. Дано:l = 2, 3 = 120°.
Найти:4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ВАС = 72°.
4*. Прямая ЕK является секущей для прямых CD и MN (ЕCD, K MN). DEK равен 65°. При каком значении угла NKE прямые CD и MN могут быть параллельными?
Вариант II
1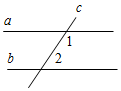 . Дано: а || b, с – секущая, 1 – 2 = 102°.
. Дано: а || b, с – секущая, 1 – 2 = 102°.
Найти: все образовавшиеся углы.
2. Дано:1 = 2, 3 = 140°.
Найти:4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если САЕ = 78°.
4*. Прямая MN является секущей для прямых АВ и CD (МАВ, NCD). Угол AMN равен 75°. При каком значении угла CNM прямые АВ и CD могут быть параллельными?
Урок40. Сумма углов треугольника
А
 1. На рисунке 1 секущей является прямая…
1. На рисунке 1 секущей является прямая…а) а; б) с; в) b; г) а или с.
Рис. 1
А2. Для угла 4 накрест лежащим будет угол…
а) 2; б) 5; в) 6; г) 7.

Рис. 2
А3. На рисунке 3 углы 1 и 2 являются…
а) односторонними; в) соответственными;
б) накрест лежащими; г) смежными.

Рис. 3
А4. Дан равносторонний треугольник BCD. Через вершину D провести прямых, параллельных прямой ВС…
а) можно две; в) нельзя ни одной;
б) можно бесконечное множество; г) можно одну.
А5. На рисунке 4 1 = 54°. Прямые а и b будут параллельными, если 2 равен…
а) 54°; б) 54° или 126°; в) 126°; г) 36°.

Рис. 4
А6. Прямые будут параллельными на рисунке:
а)
 в)
в) 
б)
 г)
г) 
Рис. 5
А7. На рисунке а, b, с пересечены секущей d. Параллельными прямыми будут прямые…
а) а и b; б) b и с; в) а и с; г) а, b и с.

Рис. 6
А8. Верным является высказывание:
а) Если две параллельные прямые пересечены третьей, то сумма накрест лежащих углов равна 180°.
б) Если при пересечении двух прямых секущей накрест лежащие углы в сумме составляют 180°, то прямые параллельны.
в) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
г) Если две прямые параллельны третьей прямой, то они перпендикулярны.
Часть 2
В1. Прямые а и b, изображенные на рисунке
, являются ______________________________________________

Рис. 7
В2. Из всех углов, изображенных на рисунке, односторонними углами являются углы _____________________

Рис. 8
В3. На рисунке 1 = 135°, 2 = 45°. Тогда прямые т и п будут ________________________________________

Рис. 9
В4. На рисунке а || b, 3 = 108°. Тогда 1 = ________________________________________________________

Рис. 10
В5. На рисунке а || b, 1 на 50° меньше 3. Тогда 2 = _______________________________________________

Рис. 11
В6. На рисунке прямые а и b – параллельны, 1 = 80°, 3 = 50°. Тогда 2 = _____________________________

Рис. 12
В7. На рисунке через вершину С треугольника BCD проведена прямая KL, параллельная стороне треугольника BD. При этом BCK = 56°, DCL = 64°. Тогда средним углом треугольника будет угол ______________________

Рис. 13
Часть 3
С1. Отрезок DМ – биссектриса треугольника CDE. Через точку М проведена прямая, пересекающая сторону DE в точке N так, что DN = MN. Вычислите градусные меры углов треугольника DМN, если CDE = 76°.
Ответы:
Часть 1
| А1 | А2 | А3 | А4 | А5 | А6 | А7 | А8 |
| в | б | а | г | а | а | г | в |
Часть 2
| В1 | В2 | В3 | В4 | В5 | В6 | В7 |
| Пересекающимися | 3 и 5, 4 и 8 | Параллельными | 108° | 65° | 30° | С = 60° |
Часть 3
С1. Возможный вариант оформления решения задачи.

1) DМ – биссектриса треугольника, поэтому CDМ = МDЕ = 38°.
2) DN = MN, поэтому треугольник DNМ является равнобедренным, а значит, МDN = DМN = 38°.
3) Углы DМN и CDМ являются накрест лежащими углами при прямых CD и МN и секущей DМ, а так как внутренние накрест лежащие углы при прямых CD и МN и секущей DМ равны, то прямые DC и МN будут параллельны.
4) Углы CDN и МND являются односторонними при параллельных прямых CD и МN и секущей DЕ, поэтому сумма углов равна 180°. А значит, DNМ = 180° – 76° = 104°.
5) Таким образом, углы треугольника DNМ будут равны 104°, 38°, 38°.
Урок38. Решение задач
| Цель деятельности учителя | Создать условия для подготовки к контрольной работе | |||
| Термины и понятия | Параллельные прямые, аксиома, свойства параллельных прямых | |||
| Планируемые результаты | ||||
| Предметные умения | Универсальные учебные действия | |||
| Умеют работать с геометрическим текстом, анализировать его, извлекать необходимую информацию | Познавательные: осуществляют логические действия. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки, осуществляют контроль по результату и способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, находить общее решение и разрешать конфликты. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений | |||
| Организация пространства | ||||
| Формы работы | Фронтальная (Ф); парная (П); индивидуальная (И) | |||
| Образовательные ресурсы | • Задания для парной работы | |||
| I этап. Актуализация опорных знаний учащихся | ||||
| Цель деятельности | Совместная деятельность | |||
| Проверить правильность выполнения домашнего задания | ( 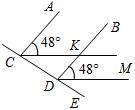 Ф/И) Ф/И)1. Ответить на вопросы учащихся по домашнему заданию и проверить правильность решения задач. 1) Так как AC || BD, CK || DM, то ACK = ВDМ = 48°. CDK + ЕDМ = 180° – ВDМ. СDK в 3 раза больше ЕDМ, тогда 3ЕDM + ЕDМ = 180° – 48°, 4EDM = 132°, EDM = 33°. Тогда KDЕ = 48° + 33° = 81°. 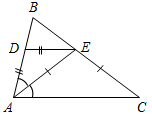 Рис. 1 Ответ: KDE = 81°. 2) АD = DЕ, тогда DАЕ = DEA. AC – биссектриса ∆ABC, тогда DAE = ЕАC, значит, EAC = DEA, следовательно, DE || АС. ∆АЕС – равнобедренный (АЕ = ЕС), тогда EAC = АСЕ = 37°, следовательно, DAC = 74°. DЕ || АС, DАС = 74°, тогда ВDЕ = 74°. Рис. 2 Ответ: BDE = 74°. | |||
| II этап. Решение задач | ||||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | ||
| Совершенствовать навыки решения задач | (П) Предлагает учащимся решить пробный вариант контрольной работы. 1. Дано:1 + 2 = 88°, а || b. Найти: все углы, образовавшиеся, при пересечении прямых а и b и секущей с. 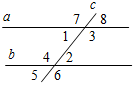 Рис. 3 2. Дано:1 + 2 = 180°, 3 = 48°. Найти:4, 5, 6. 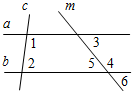 Рис. 4 3. Отрезок DM – биссектриса ∆CDE. Через точку М проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DNM, если CDE = 68°. 4. Прямая ЕK является секущей для АВ и CD (ЕАВ, KCD). AEK = 49°. При какой величине СKЕ прямые АВ и CD могут быть параллельными? | 1. а || b, тогда 1 = 2 = 44° (как накрест лежащие углы при параллельных прямых а и b и секущей с); 3 = 4 (как накрест лежащие); 1 = 3 – смежные, следовательно, 3 = 4 = 180° – 44° = = 136°; 5 = 2 = 44° (как вертикальные), 4 = 6 = 136° (как вертикальные), 1 = 8 = 44° (как вертикальные), 3 = 7 = 136°. 2. 1 и 2 – внутренние односторонние углы и по условию 1 + 2 = 180°, тогда а || b (по признаку), следовательно, 3 = 5 = 48° (как внутри накрест лежащие углы),5 = 6 (вертикальные), следовательно, 3 =5 = 6 = 48°, a 3 + 4 = 180° (односторонние), тогда 4 = 132°. 3 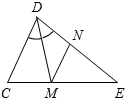 . DM – биссектриса ∆CDE, CDE = 68°, тогда CDM = MDN = . DM – биссектриса ∆CDE, CDE = 68°, тогда CDM = MDN == 34°. CD || MN, тогда DMN = CDM = 34°. CD || MN, тогда NDC + DNM = 180°. Значит, DNM = 180° – NDC = 112°. Рис. 5 Ответ: NDM = NMD = 34°, DNM = 112°. 4. 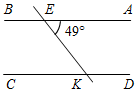 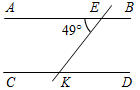 а) Рис. 6 б) Возможны два случая: а) АЕK = CKЕ, СKЕ = 49°, так как АВ || CD. б) АЕK + СKЕ = 180°, так как АВ || СD, тогда CKE = 131° | ||
| III этап. Итоги урока. Рефлексия | ||||
| Деятельность учителя | Деятельность учащихся | |||
| (Ф/И) – Продолжите фразы: • Я научился… • Я понял… • Я смогу… | (И) Домашнее задание: повторить теоретический материал, подготовиться к контрольной работе | |||
Урок39. Контрольная работа № 3
| Цель деятельности учителя | Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала | ||
| Термины и понятия | Признаки параллельности прямых; свойства параллельных прямых | ||
| Планируемые результаты | |||
| Предметные умения | Универсальные учебные действия | ||
| Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности | Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям. Регулятивные: вносят необходимые коррективы в действие после его завершения на основе учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: осознают важность и необходимость изучения предмета | ||
| Организация пространства | |||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | ||
| Образовательные ресурсы | • Задания для контрольной работы | ||
| I этап. Выполнение контрольной работы | |||
| Цель деятельности | Задания для контрольной работы | ||
| Проверить знания, умения и навыки по изученной теме | (И) Учащиеся выполняют контрольную работу (см. Ресурсный материал) | ||
| II этап. Итоги урока. Рефлексия | |||
| Деятельность учителя | Деятельность учащихся | ||
| (Ф/И) – Что выполняли на уроке? – Какие задания вызвали затруднения? Почему? – Как оцениваете свою работу на уроке? | (И) Домашнее задание: повторить пункты 5–29 | ||
Ресурсный материал
Контрольная работа
В
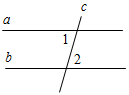 ариант I
ариант I1. Дано: а || b, с – секущая, 1 + 2 = 102°.
Найти: все образовавшиеся углы.

2. Дано:l = 2, 3 = 120°.
Найти:4.
3. Отрезок AD – биссектриса треугольника ABC. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найти углы треугольника ADF, если ВАС = 72°.
4*. Прямая ЕK является секущей для прямых CD и MN (ЕCD, K MN). DEK равен 65°. При каком значении угла NKE прямые CD и MN могут быть параллельными?
Вариант II
1
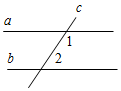 . Дано: а || b, с – секущая, 1 – 2 = 102°.
. Дано: а || b, с – секущая, 1 – 2 = 102°.Найти: все образовавшиеся углы.

2. Дано:1 = 2, 3 = 140°.
Найти:4.
3. Отрезок АK – биссектриса треугольника САЕ. Через точку K проведена прямая, параллельная стороне СА и пересекающая сторону АЕ в точке N. Найдите углы треугольника AKN, если САЕ = 78°.
4*. Прямая MN является секущей для прямых АВ и CD (МАВ, NCD). Угол AMN равен 75°. При каком значении угла CNM прямые АВ и CD могут быть параллельными?
Урок40. Сумма углов треугольника
| Цель деятельности учителя | Создать условия для доказательства теоремы о сумме углов треугольника, следствия из нее; для введения понятий остроугольного, прямоугольного и тупоугольного треугольников; для рассмотрения задачи на применение доказанных утверждений | |
| Термины и понятия | Треугольник, противолежащий угол, противолежащая сторона, прилежащий угол и сторона, остроугольный треугольник, тупоугольный, прямоугольный треугольник | |
| Планируемые результаты | ||
| Предметные умения | Универсальные учебные действия | |
| Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев; умеют отличать гипотезу от факта. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют критичность мышления | |
| Организация пространства | ||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |
| Образовательные ресурсы | • Чертежи к задачам | |