ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 22.11.2023
Просмотров: 431
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
| I этап. Анализ результатов контрольной работы | ||
| Цель деятельности | Совместная деятельность | |
| Проанализировать и откорректировать ошибки, допущенные в контрольной работе | (Ф/И) 1. Проанализировать характерные ошибки, допущенные в контрольной работе. 2. Выполнить работу над ошибками | |
| II этап. Учебно-познавательная деятельность | ||
| Цель деятельности | Постановка учебной задачи | |
| Подготовить к восприятию нового материала | (И) Решение задач по готовым чертежам. Учащимся дается 2–3 минуты на обдумывание, а затем обсуждаются возможные варианты решений. 1) Дано: AF || BD, AB = BF, B = 30°. 2) Дано: DE || AC. Доказать: BD – биссектриса CBF. Найти: сумму углов ∆АВС. Найти:A, F, сумму углов ∆ABF. 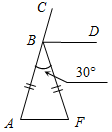 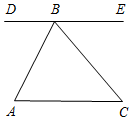 Рис. 1 Рис. 2 (Ф) После решения данных задач учитель задает вопрос, в обсуждении которого должен участвовать весь класс. – Случайно ли сумма углов треугольника АВС оказалась равной 180°, или этим свойством обладает любой треугольник? (У каждого треугольника сумма углов равна 180°.) – Это утверждение носит название теоремы о сумме углов треугольника. Итак, тема сегодняшнего урока – «Сумма углов треугольника» | |
| III этап. Изучение нового материала | ||
| Цель деятельности | Совместная деятельность | |
| Доказать теорему о сумме углов треугольника, рассмотреть следствия, ввести понятия остроугольного, тупоугольного, прямоугольного треугольников | (Ф) 1. Доказательство теоремы о сумме углов треугольника (рис. 125 учебника). 2. Решение задач № 223 (а, б, г), 225, 226 (устно). 3. Перед введением классификации треугольников по углам (п. 31) учащимся задается вопрос: «Может ли треугольник иметь: а) два прямых угла; б) два тупых угла; в) один прямой и один тупой угол?». Ответы должны быть обоснованы с помощью теоремы о сумме углов треугольника. 4. Запись в тетрадях вывода из данных ответов (следствие из теоремы о сумме углов треугольника): в любом треугольнике либо все три угла острые, либо два угла острые, а третий – тупой или прямой. 5. Ввести понятия остроугольного, тупоугольного и прямоугольного треугольников и обратить внимание учащихся на названия сторон прямоугольного треугольника – гипотенуза и катет (рис. 126 учебника, модели треугольников) | |
| IV этап. Решение задач на закрепление изученного материала | ||
| Цель деятельности | Деятельность учителя | Деятельность учащихся |
| При решении простейших задач отработать применение изученной теоремы | (Ф/И) Организует деятельность учащихся. 1. Решить задачи № 227 и 224 на доске и в тетрадях. 2. Решить задачу № 228 (а, в) на доске и в тетрадях. 3. Решить задачу № 229 на доске и в тетрадях | № 227. а) Дано:АВС, АВ = ВС, А>Вв 2 раза. Найти:А, В, С. 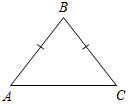 Рис. 3 Решение: Примем В = х°, следовательно, А = С = 2х°. Так как А + В + С = 180°, то 2х + х + 2х = 180°, тогда 5х = 180°, тогда х = 36°. В = 36°, А = С = 72°. б) Дано:АВС, АВ = ВС, С <BCD в 3 раза. Найти:А, В, С.  Рис. 4 Решение: Примем С = х°, следовательно, А = х°, BCD = 3х°. Так как BCD = = А + В (свойство внешнего угла), то В = 3х – х = 2х. А + В + С = 180°, тогда: х + 2х + х = 180°, 4х = 180°, х = 45°. А = С = 45°, В = 90°. № 224. Дано:АВС, А : В : С = 2 : 3 : 4. Найти:А, В, С. 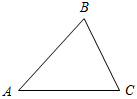 Рис. 5 Решение: Примем 1 часть – х°, следовательно, А = 2х°, В = 3х°, С = 4х°. Так как А + В + С = 180°, то 2х + 3х + 4х = 180°, тогда: 9х = 180°, х = 20°. 20° приходится на 1 часть. А = 2 · 20° = 40°, В = 3 · 20° = 60°, С = 4 · 20° = 80°. Ответ: 40°, 60°, 80°. № 228. 1) Рассмотрим два случая: а) Угол при основании равен 40°, тогда второй угол при основании равнобедренного треугольника тоже равен 40°; значит, угол при вершине равен 180° – (40° + 40°) = 100°. б) Угол при вершине равен 40°, тогда углы при основании равны (180° – 40°) : 2 = 70°. Ответ: 40°, 40°, 100° или 40°, 70°, 70°. 2) Опираемся на доказанное в задаче № 226 утверждение: углы при основании равнобедренного треугольника острые. Значит, угол при вершине равен 100°, а углы при основании равны (180° – 100°) : 2 = 40°. Ответ: 100°, 40° и 40°. № 229. Дано:АВС, АВ = ВС, AD – биссектриса А, С = 50°. Найти:АDС. 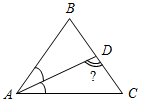 Рис. 6 Решение: 1) Так как АВС – равнобедренный, то А = С = 50°. 2) Так как AD – биссектриса А, то ВAD = DАС = 25°. 3) Рассмотрим АDС: DАС + АDС + С = 180°, тогда: 25° + АDС + 50° = 180°, АDС = 180° – 75°, АDС = 105°. Ответ: 105° |
| V этап. Итоги урока. Рефлексия | ||
| Деятельность учителя | Деятельность учащихся | |
| (Ф/И) – Что нового узнали на уроке? – Составьте синквейн к уроку | (И)Домашнее задание: изучить пункты 30–31; ответить на вопросы 1, 3, 4, 5 на с. 89; решить задачи № 223 (в), 228 (б), 230 | |
1 ... 20 21 22 23 24 25 26 27 ... 47
Урок 41. Внешний угол треугольника.
Теорема о внешнем угле треугольника
| Цели деятельности учителя | Создать условия для закрепления знаний учащихся о сумме углов треугольника при решении задач, введения понятия внешнего угла треугольника, доказательства теоремы о внешнем угле треугольника, обучения решению задач | |
| Термины и понятия | Треугольник, внешний угол, смежный угол | |
| Планируемые результаты | ||
| Предметные умения | Универсальные учебные действия | |
| Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий, умеют формулировать и доказывать теорему о внешнем угле треугольника | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач | |
| Организация пространства | ||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |
| Образовательные ресурсы | • Чертежи к задачам. • Задания для самостоятельной работы | |
| I этап. Актуализация опорных знаний учащихся | |||
| Цель деятельности | Совместная деятельность | ||
| Проверить уровень сформированности теоретических знаний | (Ф/И) 1. Один учащийся на доске доказывает теорему о сумме углов треугольника. 2. Второй учащийся решает на доске задачу из домашнего задания № 230. 3. Весь класс решает задачи по готовым чертежам (устно). – Вычислите все неизвестные углы треугольников. 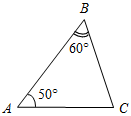 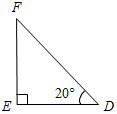 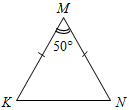 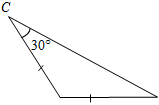 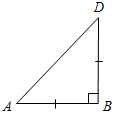 Рис. 1 Рис. 2 Рис. 3 Рис. 4 Рис. 5 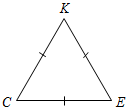 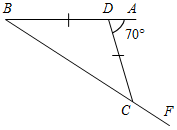 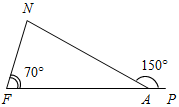 Рис. 6 Рис. 7 Рис. 8 | ||
| II этап. Изучение нового материала | |||
| Цель деятельности | Совместная деятельность | ||
| Ввести понятие внешнего угла и доказать сопутствующую теорему | (Ф/И) 1. Ввести понятие внешнего угла треугольника. 2. Доказать теорему о внешнем угле треугольника (рис. 125 учебника). 3. Решить задачу (устно). В треугольнике АВС В = 110°. Чему равны: а) сумма остальных внутренних углов треугольника; б) внешний угол при вершине В? 4. По готовому чертежу на доске устно решить задачу. Найдите внутренние углы и внешний угол СDF треугольника KСD 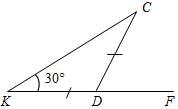 Рис. 9 | ||
| III этап. Решение задач | |||
| Цель деятельности | Деятельность учителя | Деятельность учащихся | |
| При решении простейших задач отработать изученный материал | (Ф/И) Организует деятельность учащихся. 1. Решить задачу № 232 под руководством учителя на доске и в тетрадях. 2. Рассмотреть обратное утверждение: если треугольник равнобедренный, то внешний угол при вершине, противолежащей основанию треугольника, в два раза больше угла при основании. Действительно, этот внешний угол равен сумме двух углов при основании равнобедренного треугольника, а так как углы при основании равны, то данный внешний угол в два раза больше угла при основании треугольника. 3. Решить задачу № 234 на доске и в тетрадях (рассмотреть два случая) | № 232. Дано:АВС, ВСD>А в 2 раза. Доказать:АВС – равнобедренный. 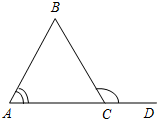 Рис. 10 Доказательство: Примем А = х, тогда ВСD = 2х. По свойству внешнего угла: ВСD = А + В, тогда 2х = х + В, тогда В = х, значит, А = В, то есть АВС – равнобедренный. Обратное утверждение верно. № 234. Дано:АВС, АВ = ВС, ВСD = 115°. Найти:А, В, С. 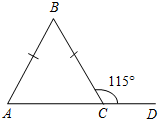 Рис. 11 Решение: 1) С, ВСD – смежные, значит, С = 180° – 115° = 65°. 2) А = С = 65° (по свойству равнобедренного треугольника). 3) В = 180° – (А + С). В = 180° – 130° = 50°. Ответ: 65°, 65°, 50°. Дано:АВС, АВ = ВС, СВD = 115°. Найти:А, В, С. 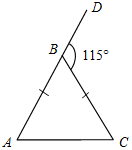 Рис. 12 Решение: 1) В, СВD – смежные, значит, В = 180° – 115° = 65°. 2) Так как А = С (по свойству равнобедренного треугольника), то А = С = (180° – 65°) : 2 = 57,5° = 57°30. Ответ: 65°, 57°30, 57°30 | |
| IV этап. Самостоятельная работа | |||
| Цель деятельности | Задания для самостоятельной работы | ||
| Совершенствовать навыки самостоятельного решения задач | (И) Работа выполняется 15–20 минут. Вариант I 1. Один из углов равнобедренного треугольника равен 96°. Найдите два других угла треугольника. 2. В треугольнике СDЕ с углом Е = 32° проведена биссектриса CF, СFD = 72°. Найдите D. Вариант II 1. Один из углов равнобедренного треугольника равен 108°. Найдите два других угла треугольника. 2. В треугольнике СDЕ проведена биссектриса CF, D = 68°, Е = 32°. Найдите СFD. Вариант III 1. В равнобедренном треугольнике MNP c основанием МР и углом N = 64° проведена высота МН. Найдите РМН. 2. В треугольнике СDЕ проведены биссектрисы CK и DР, пересекающиеся в точке F, причем DFK = 78°. Найдите СЕD. Вариант IV 1. В равнобедренном треугольнике CDЕ c основанием СЕ и D = 102° проведена высота СН. Найдите DСН. 2. В треугольнике АВС проведены биссектрисы АМ и ВN, пересекающиеся в точке K, причем АKN = 58°. Найдите АСВ | ||
| V этап. Итоги урока. Рефлексия | |||
| Деятельность учителя | Деятельность учащихся | ||
| (Ф/И) – Какой угол называется внешним углом треугольника? – Каким свойством обладает внешний угол равнобедренного треугольника? – Оцените свою работу на уроке. Поставьте себе оценку. Какие затруднения у вас возникли? | (И)Домашнее задание: изучить пункты 30–31; ответить на вопросы 1–5 на с. 88; решить задачи № 233, 235 | ||
Урок 42. Теорема о соотношениях
между сторонами и углами треугольника
| Цель деятельности учителя | Создать условия для рассмотрения теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; для обучения применению этих знаний при решении задач | |
| Термины и понятия | Треугольник, противолежащий угол, сторона | |
| Планируемые результаты | ||
| Предметные умения | Универсальные учебные действия | |
| Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач | |
| Организация пространства | ||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |
| Образовательные ресурсы | • Чертежи к задачам | |
1 ... 21 22 23 24 25 26 27 28 ... 47
| I этап. Актуализация опорных знаний учащихся | ||
| Цель деятельности | Совместная деятельность | |
| Провести анализ ошибок, допущенных в самостоятельной работе | (Ф/И) 1. Анализ результатов самостоятельной работы. 2. Обсуждение вопросов учащихся по домашнему заданию | |
| II этап. Учебно-познавательная деятельность | ||
| Цель деятельности | Совместная деятельность | |
| Рассмотреть теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем | (Ф/И) 1. Решить подготовительную задачу. Дано: ∆МОС; KМС; KМ = ОМ. Доказать: 1) 1 >3; 2) МОС>3. 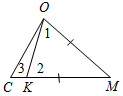 Рис. 1 Доказательство: 1) Треугольник ОМK – равнобедренный с основанием ОK, поэтому 1 = 2. Угол 2 – внешний угол треугольника ОKС, поэтому 2 >3. Значит, 1 = 2 и 2 >3, следовательно, 1 >3. 2) Так как точка K лежит на МС, то МОС>1, а так как 1 >3, то МОС>3. 2. Сформулировать и доказать первое утверждение теоремы: в треугольнике против большей стороны лежит больший угол (по рис. 127 учебника). 3. Решить задачу № 236 (устно). 4. Перед доказательством второго утверждения теоремы (в треугольнике против большего угла лежит бо́льшая сторона) напомнить учащимся, какая теорема называется обратной данной, и предложить привести примеры обратных теорем, изученных ранее. 5. Сформулировать утверждение, обратное первому утверждению (самостоятельно). 6. Доказать обратное утверждение (методом от противного). После того как сформулирована обратная теорема, записаны ее условие и заключение, полезно вспомнить, что при сравнении двух отрезков, например СD и ЕF, возможен один и только один из трех случаев: СD > ЕF; СD = ЕF; СD < EF. Поэтому если мы предполагаем, что СD не больше ЕF, то возможны два случая: либо СD = = ЕF, либо СD < ЕF. После этих предварительных рассуждений учащимся легче понять, почему при доказательстве теоремы, предположив, что АВ не больше АС, мы рассматриваем два возможных случая: либо АВ = = АС, либо АВ < АС. 7. Решить задачу № 237 (устно). 8. Доказать следствие 1 (самостоятельно). 9. Доказать следствие 2, выражающее признак равнобедренного треугольника (с помощью учителя) | |
| III этап. Решение задач | ||
| Цель деятельности | Совместная деятельность | |
| Научить применять полученные теоретические знания при решении задач | (Ф/И) 1. Решить задачи по готовым чертежам. 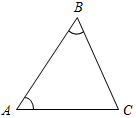 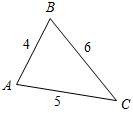 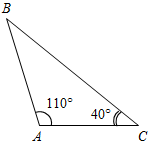 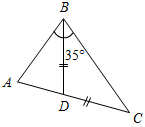 Рис. 2 Рис. 3 Рис. 4 Рис. 5 1) Дано:A = В(рис. 2). Доказать: ∆АВС – равнобедренный. 2) Сравните углы ∆АВС(рис. 3). 3) Укажите наибольшую и наименьшую стороны ∆АВС (рис. 4). 4) Сравните отрезки AD и DC (рис. 5). 2. Решить задачу № 240 на доске и в тетради. № 240. Дано:АВС, АВ = ВС, АО – биссектриса А, СО – биссектриса С. Доказать:АОС – равнобедренный. 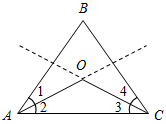 Рис. 6 Доказательство: 1) Так как АВС – равнобедренный, то А = С. 2) Так как АО, СО – биссектрисы соответственно равных углов, то 1 = 2 = 3 = 4. 3) Рассмотрим АОС: 2 = 3, тогда АО = СО, значит, АОС – равнобедренный по определению | |
| IV этап. Итоги урока. Рефлексия | ||
| Деятельность учителя | Деятельность учащихся | |
| (Ф/И) – Какие теоремы изучены на уроке? – Оцените свою работу на уроке. – Задайте три вопроса по теме урока | (И) Домашнее задание: изучить п. 33; ответить на вопросы 6–8 на с. 88; решить задачи № 239, 241 | |
Урок43. Теорема о соотношениях
между сторонами и углами треугольника.
Решение задач
| Цель деятельности учителя | Создать условия для рассмотрения теоремы о соотношениях между сторонами и углами треугольника, следствия из этих теорем; для обучения применению полученных знаний при решении задач | |
| Термины и понятия | Треугольник, противолежащий угол, сторона | |
| Планируемые результаты | ||
| Предметные умения | Универсальные учебные действия | |
| Владеют базовым понятийным аппаратом по основным разделам изучаемых понятий | Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач | |
| Организация пространства | ||
| Формы работы | Фронтальная (Ф); индивидуальная (И) | |
| Образовательные ресурсы | • Задания для проверочной работы | |
| I этап. Актуализация опорных знаний учащихся | ||
| Цель деятельности | Совместная деятельность | |
| Проверить уровень сформированности теоретических знаний по теме | (Ф/И) 1. Проверить правильность выполнения домашнего задания. 2. Провести проверочную работу (см. Ресурсный материал) | |
| II этап. Решение задач | ||
| Цель деятельности | Деятельность учителя | Деятельность учащихся |
| Совершенствовать навыки решения задач | (Ф/И) Организует деятельность учащихся: решение задач № 243, 246 у доски и в тетрадях | № 243. Дано:АВС, АА1 – биссектриса А, СD || АА1, СDАВ = D. Доказать: АС = AD. 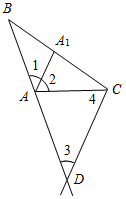 Рис. 1 Доказательство: 1) Так как СD || АА1, то 1 = 3 (как соответственные), с другой стороны, так как СD || АА1, то А1АD + 3 = 180° (по свойству параллельных прямых), 2 + САD + 3 = 180°. 2) В САD: 3 + САD + 4 = 180° (свойство углов треугольников). Сравним два равенства и получим, что 4 = 2. 3) 1 = 2 (по усл.), 1 = 3 (из п. 1), 2 = 4 (из п. 2), 3 = 4, значит, АС = AD, что и требовалось доказать. № 246. Дано:АВС, ВО и ОС – биссектрисы, ОЕ || АВ, ОD || АС. Доказать:РОЕD = BC. 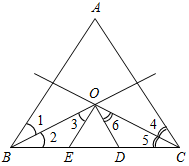 Рис. 2 Доказательство: 1) Так как ОЕ || АВ, то 1 = 3, как накрест лежащие, 1 = 2, так как ВО – биссектриса, 2 = 3, тогда ВЕ = ОЕ (свойство равнобедренного треугольника). 2) Так как ОD || АС, то 4 = 6, как накрест лежащие, 4 = 5, так как СО – биссектриса, 5 = 6, значит, CD = ОD (свойство равнобедренного треугольника). РОЕD = ОЕ + ЕD + DО || || || тогда РОЕD = BC, что и требовалось доказать ВС = ВЕ + ЕD + DС |
| III этап. Итоги урока | ||
| Деятельность учителя | Деятельность учащихся | |
| (Ф/И) – Оцените свою работу на уроке. – Задайте три вопроса по теме урока | (И) Домашнее задание: решить задачи № 244, 245 | |