Файл: Урок Прямая и отрезок.docx

Ресурсный материал

Контрольная работа

Вариант I

1. На рисунке 1 АВЕ = 104°, DСF = 76°, АС = 12 см. Найдите сторону АВ треугольника АВС.

2. В треугольнике СDЕ точка М лежит на стороне СЕ, причем СМD острый. Докажите, что DЕ >DМ.

3. Периметр равнобедренного тупоугольного треугольника равен 45 см, а одна из его сторон больше другой на 9 см. Найдите стороны треугольника.

Вариант II

1. На рисунке 2 ВАЕ = 112°, DВF = 68°, ВС = 9 см. Найдите сторону АС треугольника АВС.

2. В треугольнике MNP точка K лежит на стороне MN, причем NKP острый. Докажите, что KР <МР.

3. Одна из сторон тупоугольного равнобедренного треугольника на 17 см меньше другой. Найдите стороны этого треугольника, если его периметр равен 77 см.

Вариант III
(для более подготовленных учащихся)

1. На рисунке 1 СВМ = АСF; Р_АВС= 34 см, ВС = 12 см. Найдите сторону АС треугольника АВС.

2. В треугольнике MNK K = 37°, М = 69°, NP – биссектриса треугольника. Докажите, что МР <РK.

3. Периметр равнобедренного треугольника равен 45 см, а одна из его сторон больше другой на 12 см. Найдите стороны треугольника.

Вариант IV
(для более подготовленных учащихся)

1. На рисунке 2 ЕАМ = DВF; ВС = 17 см, Р_АВС= 45 см. Найдите сторону АВ треугольника АВС.

2. В треугольнике СDЕ Е = 76°, D = 66°, ЕK – биссектриса треугольника. Докажите, что KС >DK.

3. Периметр равнобедренного треугольника равен 50 см, а одна из его сторон на 13 см меньше другой. Найдите стороны треугольника.



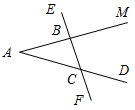
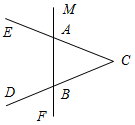
Рис. 1 Рис. 2

Урок47. Анализ ошибок контрольной работы

Цели деятельности учителя	Создать условия для устранения пробелов в знаниях учащихся; совершенствовать навыки решения задач
Термины и понятия	Треугольник, противолежащий угол, сторона, неравенство треугольника
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют работать с геометрическим текстом, точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики		Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют креативность мышления, инициативу, находчивость, активность при решении геометрических задач
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для групповой работы

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Сообщить результаты контрольной работы	(Ф) 1. Сообщить общие результаты контрольной работы. 2. Объяснить задания, с которыми не справилось большинство учащихся, или заслушать тех, кто успешно справился с этими заданиями. 3. Продемонстрировать лучшие работы
II этап. Работа над ошибками
Цель деятельности	Совместная деятельность
Устранить пробелы в знаниях учащихся	(И/Г) 1. Учащиеся находят свои ошибки, используя указания учителя или ученика, справившегося с задачами контрольной работы (можно объединить детей в небольшие группы в зависимости от уровня и варианта контрольной работы, в этом случае им будет легче находить свои ошибки). 2. Учащиеся решают другой вариант контрольной работы или переходят к решению задач следующего уровня (по выбору). Если ученик успешно справился с задачами контрольной работы, он решает дополнительные задачи. 3. Более подготовленным учащимся можно предложить решить дополнительные задачи. Задача 1. На сторонах угла А, равного 127°, отмечены точки В и С, а внутри угла – точка D так, что ABD = 25°, a ACD = 19°. Найти угол BDC. 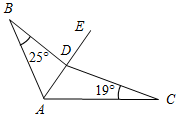Рис. 1 Задача 2. Треугольники ABC и ADC имеют общую сторону АС. Отрезок BD пересекает отрезок АС. Известно, что BD = AD = CD. Докажите, что ∆ADC является тупоугольным, если ABC = 130°. 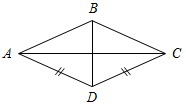Рис. 2 Задача 3. В равнобедренном треугольнике АВС угол В равен 100°. Внутри треугольника взята такая точка М, что МАВ = 10°, МВА = 20°. Найдите угол ВМС. 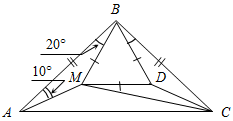Рис. 3
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Задайте три вопроса по задачам. – Оцените свою работу. – Какие трудности у вас возникли?		(И) Домашнее задание: можно предложить учащимся на выбор поменяться вариантами контрольной работы или решить дополнительные задачи

---

Урок48. Некоторые свойства прямоугольных треугольников

Цель деятельности учителя	Создать условия для рассмотрения свойств прямоугольных треугольников, обучения решению задач на применение свойств прямоугольных треугольников
Термины и понятия	Треугольник, противолежащий угол, катеты, гипотенуза
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания		Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для самостоятельной, групповой работы. • Чертежи к задачам

1   ...   24   25   26   27   28   29   30   31   ...   47

---

I этап. Мотивация к деятельности
Цель деятельности	Совместная деятельность
Подготовить учащихся к восприятию новой темы	(Ф/И) Организует деятельность учащихся. 1. Решить задачи по готовым чертежам. 1) Найти:A, C. 2) Дано:A : B = 1 : 2. 3) Доказать: AD = АВ. Найти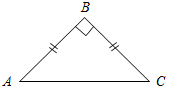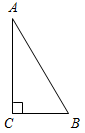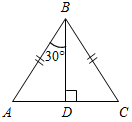:A, B. Рис. 1 Рис. 2 Рис. 3
II этап. Учебно-познавательная деятельность
Цель деятельности	Задания для самостоятельной работы
Рассмотреть свойства прямоугольных тре-угольников	(Ф/И) Можно сформулировать свойства прямоугольного треугольника в виде задач на доказательство и предложить учащимся решить их самостоятельно. (Задачу 1 можно предложить менее подготовленным учащимся, остальных детей разделить на два варианта и предложить варианту I решить задачу 2, варианту II – задачу 3. На решение задачи отводится 5–7 минут. Через 2–3 минуты от начала решения можно дать подсказку для решения задач 2 и 3: достройте свой треугольник до равностороннего с боковой стороной, равной гипотенузе.) Задача 1. Докажите, что в прямоугольном треугольнике сумма острых углов равна 90°. Задача 2. Докажите, что в прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы. Задача 3. Докажите, что если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 30°. Необходимо заслушать различные способы решения данных задач, выбрать наиболее рациональный способ и отметить, что эти три утверждения являются свойствами прямоугольных треугольников
III этап. Решение задач на закрепление изученного материала
Цель деятельности	Деятельность учителя	Деятельность учащихся
Научить применять изученные свойства при решении задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачи по готовым чертежам на доске (устно). 1) Дано: ∆АВС. Найти: углы ∆АВС. 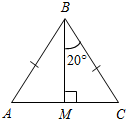Рис. 6 2) Дано: а || b. Найти: углы ∆MON. 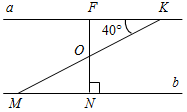Рис. 7 2. Решить задачу № 254 (устно). 3. Решить задачу № 255 на доске и в тетрадях. 4. Решить задачу № 257 на доске и в тетрадях. (П) 5. Решить задачу № 260 (в парах). (Г) 6. Решить задачи. Задача 1. Найти углы прямоугольного треугольника, если угол между биссектрисой и высотой, проведенными из вершины прямого угла, равен 15°. Задача 2. В равнобедренном треугольнике один из углов равен 120°, а основание равно 4 см. Найдите высоту, проведенную к боковой стороне	№ 254. Дано:АВС – равнобедренный, С = 90°, А = В. Найти:А, В. 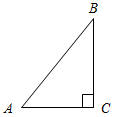Рис. 4 Решение: 1) А + В = 90° (свойство прямоугольного треугольника), А = В, следовательно, А = В = 90° : 2 = 45°. Ответ: 45°, 45°. № 255. Дано:CDЕ – равнобедренный, CD = DЕ, CF – высота, D = 54°. Найти:ЕСF. 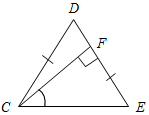Рис. 5 Решение: 1) Так как CD = DЕ, то С = Е.С + Е = 180° – D (по свойству суммы углов треугольника); С + Е = 180° – 54°, С = Е = 126° : 2 = 63°. 2) FСD = 90° – D (по свойству прямоугольного треугольника); FСD = 90° – 54° = 26°. 3) ЕСF = С – FСD, ЕСF = 63° – 26° = 37°. Ответ: 37°. № 257. Дано:АВС, С = 90°, внешний угол при А = 120°, АС + АВ = 18 см. Найти: АС, АВ. 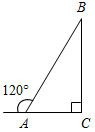Рис. 8 Решение: 1) По свойству смежных углов, ВАС = 180° – 120° = 60°. 2) В = 90° – А (по свойству прямоугольного треугольника), В = 90° – 60° = = 30°, и тогда, по свойству прямоугольного треугольника АС = АВ. 3) АС + АВ = 18, АВ = 2АС, тогда АС + 2АС = 18, тогда АС = 6 см. АВ = 2 · 6 = 12 см. Ответ: 6 см, 12 см. № 260. Дано:АВС – равнобедренный, АВ = ВС = 15,2 см, ВВ1 – высота, ВВ1 = 7,6 см. Найти: углы АВС. 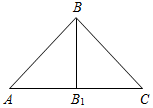Рис. 9 Решение: 1) ВВ1 = ВС, так как 7,6 = · 15,2, значит, по свойству прямоугольного тре-угольника, ВСВ1 = 30°. 2) Так как АВС – равнобедренный, то ВАС также 30°, а АВС = 180° – – А – С = 180° – 30° – 30° = 120°. Ответ: 30°, 30°, 120°. Задача 1. 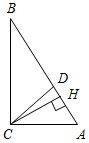Рис. 10 Решение: CD – биссектриса, СН – высота, DCH = 15°, DCA = 45°, тогда НСА = 30°. ∆НСА – прямоугольный, в нем НСА = 30°, тогда САН = 60°. ∆АВС – прямоугольный, в нем A = 60°, тогда В = 30°. Ответ: 30°, 60°, 90°. Задача 2. 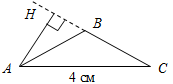Рис. 11 Решение: 120° – угол при вершине равнобедренного треугольника, тогда A = C = 30°. АН – высота ∆АВС, тогда ∆АНС – прямоугольный, в нем C = 30°, значит, АН = АС = 2 см. Ответ: 2 см
IV этап. Итоги урока
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какие свойства прямоугольных треугольников узнали на уроке? – Оцените свою работу на уроке и работу своих товарищей в группе		(И) Домашнее задание: выучить материал пунктов 30–35; ответить на вопросы 1–9 на с. 88; решить задачи № 242, 250 (б, в)

---

Урок49. Некоторые свойства прямоугольных треугольников.
Решение задач

Цели деятельности учителя	Создать условия для закрепления основных свойств прямоугольных треугольников, рассмотрения признака прямоугольного треугольника и свойства медианы прямоугольного треугольника; совершенствовать навыки решения задач на применение свойств прямоугольного треугольника
Термины и понятия	Треугольник, противолежащий угол, катеты, гипотенуза
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания		Познавательные: умеют выдвигать гипотезы при решении учебных задач и понимают необходимость их проверки. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для фронтальной работы

1   ...   25   26   27   28   29   30   31   32   ...   47

---