Файл: Урок Прямая и отрезок.docx

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить теоретическую подготовленность учащихся	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Заполнить пропуски в решении задач. 1) В равнобедренном треугольнике один из внешних углов равен 60°, высота, проведенная к боковой стороне, равна 5 см. Найдите основание треугольника. 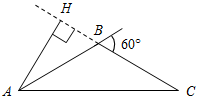Рис. 1 Решение: Так как внешний угол равен 60°, то смежный с ним внутренний угол равен ... Этот угол может быть только углом, противолежащим основанию, так как он ... Так как ∆АВС – равнобедренный с основанием AС, то А = ... = ... Так как АН – высота, то ∆АНС – ... В ∆АНСC = 30°, значит, АН = ... Так как АН = 5 см, то АС = ... Ответ: АС = ... 2) Высота и медиана, проведенные из одной вершины треугольника, разделили его угол на три равные части. Найдите углы треугольника. 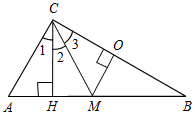Рис. 2 Решение: Пусть СН – высота, СМ – медиана ∆АВС, 1 = 2 = 3. Проведем ОМСВ, тогда ∆АСН = ∆МСН по ... ∆СМН = ∆СМО по ... Тогда АН = НМ = МО = МА = МВ. Ответ: А = 60°, B = 30°, C = 90°. После обсуждения нужно отметить, что эти две задачи характеризуют дополнительные свойства прямоугольных треугольников: 1) Свойство медианы прямоугольного треугольника, проведенной из вершины прямого угла: В прямоугольном треугольнике медиана, проведенная из вершины прямого угла, равна половине гипотенузы. 2) Признак прямоугольного треугольника: Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный
II этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки решения задач	(Ф/И) Организует деятельность учащихся. 1. Решение задачи с подробным обсуждением: Гипотенуза прямоугольного треугольника в четыре раза больше проведенной к ней высоты. Найдите острые углы треугольника. (Г) 2. Самостоятельное решение задач с последующей самопроверкой по готовым ответам. 1) Найти: ВС. 2) Найти: АВ. 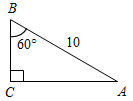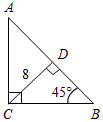Рис. 4 Рис. 5 3) Найти: АЕ. 4) Найти:B, D. 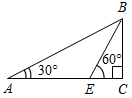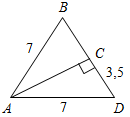Рис. 6 Рис. 7 5) Найти:СЕ, РС. 6) Найти: СА1. 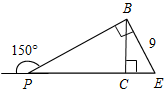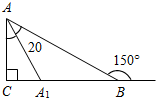Рис. 8 Рис. 9 7) Найти:MCA. 8) Найти:A, ABC. 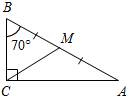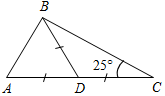Рис. 10 Рис. 11		1. 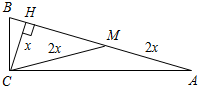Рис. 3 Решение: СН – высота. Пусть СН = х, тогда АВ = 4х. Проведем медиану СМ, СМ = АВ = 2х, ВМ = АМ = 2х. В ∆СНМH = 90°, СН = х, СМ = 2х, тогда НМС = 30°, следовательно, AMC = 150°. ∆АМС – равнобедренный, тогда A = MCA = 15°. ∆ABC – прямоугольный, A = 15°, тогда B = 75°. Ответ: 15°, 75°. 2. Ответы для самопроверки. 1) ВС = 5. 2) АВ = 16. 3) АЕ = 14. 4) В = D = 60°. 5) СЕ = 4,5, РС = 13,5. 6) СА1 = 10. 7) MCA = 20°. 8) А = 65°, ABC = 90°
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какие свойства прямоугольного треугольника узнали на уроке? – Сформулируйте признак прямоугольного треугольника. – Оцените свою работу в группе. – Какие затруднения возникли?		(И)Домашнее задание (дано на карточке): решить задачи. 1) Найти:CAD. 2) Найти: AD. 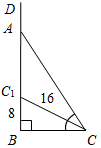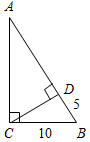3) Найти: BF. 4) Найти: MD.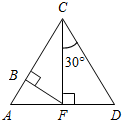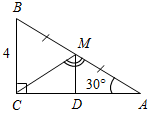

---

Урок50. Признаки равенства прямоугольных треугольников

Цели деятельности учителя	Создать условия для доказательства признаков равенства прямоугольных треугольников и демонстрации их применения при решении задач
Термины и понятия	Треугольник, противолежащий угол, катеты, гипотенуза
Планируемые результаты
Предметные умения		Универсальные учебные действия
Владеют базовым понятийным аппаратом по основным разделам содержания		Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы, понимать и использовать математические средства наглядности. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной работы

1   ...   26   27   28   29   30   31   32   33   ...   47

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить уровень усвоения теоретического материала	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Сформулировать свойства прямоугольных треугольников. 3. Вспомнить признаки равенства треугольников. 4. Решить задачу. Гипотенузы ВD и АС прямоугольных треугольников ВАD и АВС с общим катетом АВ и с равными катетами АD и ВС пересекаются в точке О. Докажите, что треугольник АОВ равнобедренный. 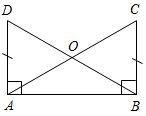Рис. 1 5. Заполнить пропуски в решении задачи. Высота и медиана, проведенные из одной вершины треугольника, разделили его угол на три равные части. Найдите углы треугольника. Решение: Пусть СН – высота, СМ – медиана АВС, 1 = 2 = 3. Проведем ОМСВ, тогда ∆АСН = ∆МСН по ... ∆СМН = ∆СМО по … Тогда АН = НМ = МО = 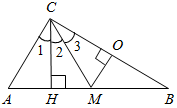МА = МВ. Рис. 2 Ответ: А = 60°, B = 30°, C = 90°
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Рассмотреть и доказать признаки равенства прямоугольных треугольников	(Ф/И) 1. Доказательство признаков равенства прямоугольных треугольников по двум катетам, по катету и прилежащему острому углу, по гипотенузе и острому углу с опорой на признаки равенства треугольников (устно;самостоятельно). 2. Доказательство признака равенства прямоугольных треугольников по гипотенузе и острому углу по моделям равных прямоугольных треугольников (устно). 3. Доказательство признака равенства прямоугольных треугольников по гипотенузе и катету (по рис. 133 учебника) (проводит учитель, так как доказательство этого признака требует дополнительных построений и непростых логических рассуждений)
III этап. Учебно-познавательная деятельность
Цель деятельности	Деятельность учителя	Деятельность учащихся
Научить применять изученные признаки при решении задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 261 на доске и в тет- радях. 2. Сформулировать и доказать признак равенства прямоугольных треугольников по катету и противолежащему углу (задача № 268) (самостоятельно). 3. Решить задачу № 269 на доске и в тет- радях. 4. Решить задачу. Докажите, что если треугольник прямоугольный, то медиана, проведенная из вершины прямого угла, равна половине гипотенузы. 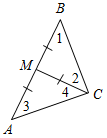Рис. 4 Доказательство: СВМ – равнобедренный. СМА – равнобедренный (по усл.), следо-вательно, по свойству равнобедренного треугольника 1 = 2, 3 = 4. 1 + 2 + 3 + 4 = 180°, 22 + 24 = = 180°, 2 + 4 = 90°, следовательно, АВС – прямоугольный. 5. Решить задачу. Дано: СМ = ВМ = МА. Доказать: ∆АВС – прямоугольный. 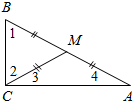Рис. 5 Доказательство: Пусть СМ ≠ МА и СМ ≠ MB. Для определенности пусть СМ>МА, тогда СМ>MB, следовательно, 4 >3, l >2, но l + 4 = 90°, тогда 2 + 3 < 90°, что противоречит тому, что C = 90°. Таким же образом можно получить противоречие для случая СМ<МА, СМ <MB. Значит, СМ = МА = MB. После обсуждения нужно отметить, что эти две задачи иллюстрируют свойства прямоугольных треугольников	№ 261. Дано:АВС – равнобедренный, АВ = ВС, АA1, СС1 – высоты. Доказать:АA1 = СС1. 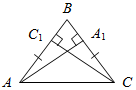Рис. 3 Доказательство: 1) А1АС = 90° – А1СА || || тогда А1АС = С1СА1. ССА = 90° – С1АС 2) А1АС и С1СА: АС – общая, А1АС = С1СА (из п. 1), С1АС = А1СА (АВ = ВС). А1АС = С1СА (по стороне и двум прилежащим углам), тогда АA1 = СС1 (по определению равных треугольников), что и требовалось доказать. № 268. Дано:АВС и А1В1С1, С = С1 = 90°, В = В1, АС = А1С1. Доказать:АВС = А1В1С1. 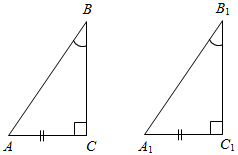Рис. 6 Доказательство: 1) А = 90° – В || || тогда А = А1, А1 = 90° –В1 2) Рассмотрим АВС и А1В1С1. АС = А1С1 (по усл.), С = С1 (по усл.), А = А1 (из п. 1), следовательно, АВС = А1В1С1, что и требовалось доказать. № 269. Дано:АВС и А1В1С1, А = А1, В = В1, ВН, В1Н1 – высоты, ВН = В1Н1. Доказать:АВС = А1В1С1. 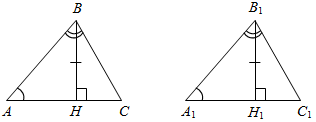Рис. 7 Доказательство: 1) Рассмотрим АВН и А1В1Н1. ВН = В1Н1, А = А1, следовательно, АВН = А1В1Н1 (по катету и острому углу), тогда АВ = А1В1, (по определению равных треугольников). 2) Рассмотрим АВС и А1В1С1. АВ = А1В1, (из п. 1), А = А1 (по усл.), В = В1 (по усл.), следовательно, АВС = А1В1С1 (по стороне и прилежащим углам)
IV этап. Итоги урока. Рефлексия
Деятельность учителя			Деятельность учащихся
(Ф/И) – Перечислите свойства прямоугольных треугольников. – Перечислите признаки равенства прямоугольных треугольников. – Оцените свою работу на уроке. – Составьте синквейн к уроку			(И) Домашнее задание: изучить п. 36; ответить на вопросы 12–13 на с. 88–89; решить задачи № 262, 264

---

Урок 51. Решение задач

Цель деятельности учителя	Создать условия для обучения применению признаков равенства прямоугольных треугольников и их свойств при решении задач, для выработки умения решать задачи; способствовать развитию умения логически мыслить
Термины и понятия	Треугольник, противолежащий угол, катеты, гипотенуза
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач		Познавательные: умеют устанавливать причинно-следственные связи, строить логическое рассуждение, делать умозаключения и выводы; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, в парах, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); парная (П); индивидуальная (И)
Образовательные ресурсы	• Чертежи к задачам. • Задания для самостоятельной работы

1   ...   27   28   29   30   31   32   33   34   ...   47

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать теоретические знания	(Ф/И) 1. Ответить на вопросы учащихся по домашнему заданию. 2. Сформулировать свойства прямоугольных треугольников. 3. Сформулировать признаки равенства прямоугольных треугольников. 4. Устно решить задачи по готовым чертежам. 1) На рисунке 1 В = С =90°; 1 = 2. Докажите, что АВ = СD. 2) На рисунке 2 АВ = СD; ВС = АD, АFВ = СЕD = 90°. Докажите, что BF = ED; АF = EC. 3) На рисунке 3 1 = 2 = 90°, АВ = DС. Докажите, что ВС = АD. 4) На рисунке 4 АН и А1Н1 – высоты треугольников АВС и А1В1С1; АС = А1С1; 1 = 2; АН = А1Н1. Докажите, что ∆АВС = ∆А1В1С1. 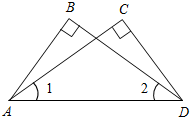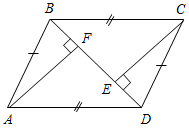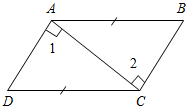Рис. 1 Рис. 2 Рис. 3 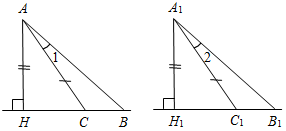Рис. 4
II этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
Совершенствовать навыки решения задач по изученной теме	(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 263 на доске и в тетрадях. 2. Решить задачу № 267 на доске и в тетрадях. (П) 3. Решить задачи по готовым чертежам. 1) Доказать: ВСCD. 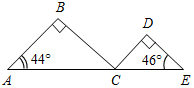Рис. 5 2) Найти:АСЕ. 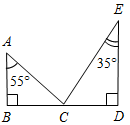Рис. 6 3) Дано: ВН = 4 см. Найти: АН. 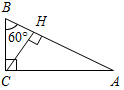Рис. 7 4) Дано: АВ || CD. Найти: углы ∆CDO. 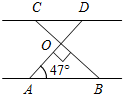Рис. 8 5) Дано: О – общая середина АВ и CD, АВCD. Доказать: АС = DB. 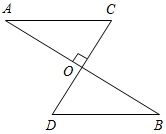Рис. 9 6) Доказать: МС – медиана ∆KMN. 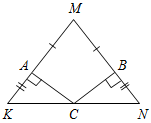Рис. 10 7) Дано: BD – биссектриса АВС. Доказать: DB – биссектриса ADC. 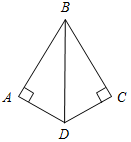Рис. 11 8) Дано: ВМ = 5 см. Найти: ME. 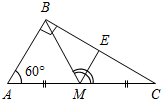Рис. 12	№ 263. Дано:АВС – равнобедренный, АВ = АС; СС1, ВВ1 – высоты, ВВ1СС1 = М, ВМС = 140°. Найти:А, В, С. 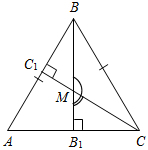Рис. 13 Решение: 1) По свойству смежных углов, 180° – 140° = СМВ1. СМВ1 = 40°, тогда В1СМ (ВСС1) = 90° – 40° = 50°. 2) А = 90° – В1СС1 = 90° – 50° = 40°. 3) По свойству углов в треугольнике, В + С = 180° – А, В + С = 180° – 40° = 140°. Так как В = С (АВ = АС), то В = 70°, С = 70°. Ответ: 40°, 70°, 70°. № 267. Дано:AВC и A1В1C1, СС2, ВВ2, С1М1, В1N1 – высоты; ВВ2 = В1N1, СС2 = С1М1, ВС = В1C1. Доказать:AВC = A1В1C1. 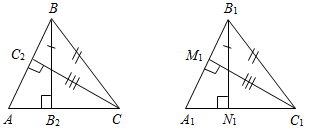Рис. 14 Доказательство: 1) Рассмотрим В2ВС и N1В1С1. ВС = В1C1 (по усл.), ВВ2 = В1N1 (по усл.), следовательно, В2ВС = N1В1С1 (по гипотенузе и катету), тогда С = С1 (по определению равных треугольников). 2) Рассмотрим С2ВС и М1В1С1. ВС = В1C1 (по усл.), СС2 = С1М1 (по усл.), следовательно, С2ВС = М1В1С1, (по гипотенузе и катету), тогда В = В1 (по определению равных треугольников). 3) Рассмотрим AВC и A1В1C1. ВС = В1C1 (по усл.), В = В1 (из п. 2), С = С1 (из п. 1), тогда AВC = = A1В1C1 (по стороне и двум прилежащим углам)
III этап. Вариант_I'>Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень усвоения теоретического материала и умение применять его при решении задач	(И) Учащиеся выполняют задания самостоятельной работы (см. Ресурсный материал)
IV этап. Итог урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Перечислите свойства прямоугольного треугольника, которые применили при решении задач самостоятельной работы. – Оцените свою работу и работу своего напарника		(И) Домашнее задание: повторить п. 30–36, подготовиться к устному опросу; решить задачи № 258, 265

---