Файл: Урок Прямая и отрезок.docx

Ресурсный материал

Самостоятельная работа

Вариант I

1. На рисунке 1 АD = DС; ЕD = DF; 1 = 2 = 90°. Докажите,что треугольник АВС равнобедренный.

2. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 18 см. Найдите гипотенузу и меньший катет.

Вариант II

1. На рисунке 2 1 = 2, 3 = 4 = 90°; ВD = DС. Докажите, что треугольник АВС равнобедренный.

2. Один из острых углов прямоугольного треугольника в два раза меньше другого, а разность гипотенузы и меньшего катета равна 15 см. Найдите гипотенузу и меньший катет.

Вариант III
(для более подготовленных учащихся)

1. Через середину отрезка АВ проведена прямая а. Из точек А и В к прямой а проведены перпендикуляры АС и ВD. Докажите, что АС = ВD.

2. В прямоугольном треугольнике СDЕ с прямым углом Е проведена высота EF. Найдите CF и FD, если СD = 18 см, а DСЕ = 30°.

Вариант IV
(для более подготовленных учащихся)

1. Из точки М биссектрисы неразвернутого угла О проведены перпендикуляры МА и МВ к сторонам этого угла. Докажите, что МА = МВ.

2. В прямоугольном треугольнике АВС с гипотенузой АВ и А = 60° проведена высота СН. Найдите ВН, если АН = 6 см.



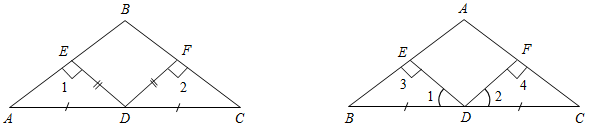
Рис. 1 Рис. 2

Урок52. Решение задач

Цель деятельности учителя	Создать условия для повторения и систематизации ранее изученного материала, выработки навыков решения задач; способствовать развитию логического мышления учащихся
Термины и понятия	Треугольник, противолежащий угол, катеты, гипотенуза
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, результаты, методы для решения задач		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения, работать в группе. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для индивидуальной, групповой работы

1   ...   28   29   30   31   32   33   34   35   ...   47

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проанализировать ошибки, допущенные в самостоятельной работе	(Ф/И) 1. Указать ошибки, допущенные в самостоятельной работе. 2. Решить задачи, вызвавшие затруднения у учащихся
II этап. Устный опрос
Цель деятельности	Задания для индивидуальной работы
Привести в систему знания учащихся по теме «Прямоугольный тре-угольник»	(Ф) К доске вызываются четверо учащихся, которые работают по карточкам (см. Ресурсный материал). Одновременно учитель проводит беседу с классом, задавая вопросы по теории
III этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
Совершенствовать навыки решения задач	(Г) Организует деятельность учащихся: решение задач № 299 и 311. Дополнительнаязадача: Через середину стороны АВ треугольника АВС проведена прямая, перпендикулярная к АВ, пересекающая ВС в точке Е. ВС = 24 см, периметр треугольника АЕС равен 30 см. Найдите АС. Выполнив задание в группах, учащиеся представляют свои решения, обсуждают и записывают в тетрадях	№ 299. Дано: АВ = АС, АР = PQ = QR = RB = ВC. Найти:А. 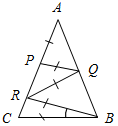Решение: 1) Примем С = В = х, так как АВС равнобедренный. Примем СВR = у. Рассмотрим RQВ: R + Q + В = 180°. 180° – х + х – у + х – у = 180° х = 2у х = 4у 2) Рассмотрим АВС: А + В + С = 180°. 4у + 4у + у = 180° 9у = 180° у = 20° 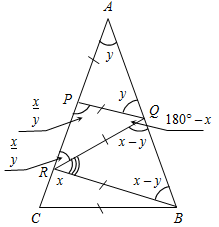Рис. 1 Ответ: А = 20°. № 311. 1) Проведем биссектрисы углов, образованных при пересечении двух прямых ОА и ОВ. Возьмем произвольную точку С на биссектрисе АОВ. ОDC = ОЕС по гипотенузе (ОС – общая гипотенуза) и острому углу (1 = 2), следовательно, CD = СЕ. 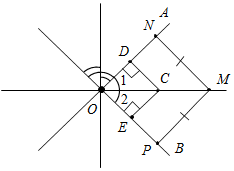Рис. 2 2) Проведем перпендикуляры MN и МР к прямым ОА и ОВ. ОNM = ОРМ по катету и гипотенузе (ОМ – общая гипотенуза, MN = МР, так как по условию точка М равноудалена от сторон ОА и ОВ). Следовательно, NОM = РОМ, то есть луч ОМ – биссектриса АОВ. Из доказанных утверждений следует, что искомое множество точек состоит из двух прямых, содержащих биссектрисы углов, образованных при пересечении данных прямых. Дополнительная задача. Решение: ∆АЕМ = ∆ВЕМ по двум катетам, тогда АЕ = ВЕ. РАЕС = АС + АЕ + СЕ, но так как АЕ = BE, то РАЕС = АС + (BE + СЕ) = АС + СВ = = АС + 24 = 30, отсюда АС = 6 см. 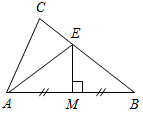Рис. 3 Ответ: АС = 6 см
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Какие цели были поставлены на уроке? Добились мы их? – Оцените свою работу и работу группы		(И) Домашнее задание: повторить пункты 15–36; решить задачи № 266, 297; принести циркули и линейки

---

Ресурсный материал

Карточки для индивидуальной работы

Вариант I

1. Сформулируйте теорему о сумме углов треугольника.

2. Один из углов при основании равнобедренного треугольника равен 65°. Найдите остальные углы треугольника.

3. В треугольнике АВС В = 110°; биссектрисы углов А и С пересекаются в точке О. Найдите угол АОС.

Вариант II

1. Сформулируйте свойство катета прямоугольного треугольника, лежащего против угла в 30°.

2. В прямоугольном треугольнике АВС С = 90°; В = 60°, АВ = 15 см. Найдите ВС.

3. Один из углов прямоугольного треугольника равен 60°, а сумма гипотенузы и меньшего катета равна 42 см. Найдите гипотенузу.

Вариант III

1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и катету.

2. В треугольниках АВС и А₁В₁С₁В =В₁ = 90°; АВ = А₁В₁, АС = А₁С₁. Найдите углы А₁ и С₁ треугольника А₁В₁С₁, если А = 34°, С = 54°.

3. На сторонах угла А отмечены точки В и С так, что АВ = АС. Через точки В и С проведены прямые, перпендикулярные соответственно сторонам АВ и АС данного угла и пересекающиеся в точке М. Докажите, что МВ = МС.

Вариант IV

1. Сформулируйте признак равенства прямоугольных треугольников по гипотенузе и острому углу.

2. В треугольниках АВС и А₁В₁С₁углы В и В₁прямые, А = А₁, АС = А₁С₁. Найдите стороны В₁С₁ и А₁В₁треугольника А₁В₁С₁, если ВС = 17 см, АВ = 12 см.

3. Даны два равных прямоугольных треугольника АВС и А₁В₁С₁, у которых В =В₁ = 90°; ВН и В₁Н₁ – высоты. Докажите, что ΔВНС = ∆В₁Н₁С₁.

Урок53. Расстояние от точки до прямой.
Расстояние между параллельными прямыми

---

Цель деятельности учителя	Создать условия для введения понятия расстояния от точки до прямой и расстояния между параллельными прямыми, для демонстрации применения данных понятий при решении задач
Термины и понятия	Параллельные прямые, расстояние от точки до прямой, перпендикуляр, наклонная
Планируемые результаты
Предметные умения		Универсальные учебные действия
Знают, какой отрезок называется наклонной, проведенной из данной точки к данной прямой, что называется расстоянием от точки до прямой и расстоянием между двумя параллельными прямыми		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной работы

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Проверить правильность выполнения домашнего задания	(Ф/И) Двое учеников по желанию выполняют на доске решение домашних задач. № 266. Дано:О, ОА = ОВ, АА1 = ВВ1, АА1ВВ1 = С. Доказать: ОС – биссектриса. 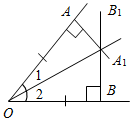Рис. 1 Доказательство: Рассмотрим ОАС и ОВС. ОС – общая, ОА = ОВ (по усл.), следовательно, ОАС = ОВС (по катету и гипотенузе), тогда 1 = 2 (по определению равных треугольников), тогда ОС – биссектриса. № 297. Дано:АDС, BAD, ВВ1 – биссектриса, BD = ВС, D = ВСD. Доказать:ВВ1 || DC. 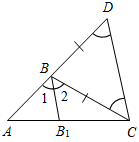Рис. 2 Доказательство: 1) D + BСD = 180° – DВC || || D + С = 1 + 2. 1 + 2 = 180° – DВC Так как D = С, 1 = 2, то D = С = 1 = 2. 2) С и 2 – накрест лежащие при ВВ1 и DC и секущей ВС, тогда ВВ1 || DC, что и требовалось доказать
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Ввести понятия расстояния от точки до прямой и расстояния между параллельными прямыми	(Ф/И) 1. Ввести понятие расстояния от точки до прямой. 1) Понятие наклонной – отрезок АВ и ВD. 2) Перпендикуляр АС, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой. 3) Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой. 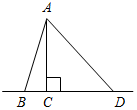Рис. 3 2. Рассмотреть рисунок 137 из учебника на с. 81. 3. Рассмотреть одно из важнейших свойств параллельных прямых: разобрать доказательство теоремы «Все точки каждой из двух параллельных прямых равноудалены от другой прямой» по рис. 138. 4. Ввести понятие расстояния между параллельными прямыми: расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми. 5. Рассмотреть утверждение, обратное доказанной теореме. Оно лежит в основе конструкции рейсмуса, применяемого в столярном деле для разметки прямых, параллельных краю бруска (см. рис. 139 учебника)
III этап. Закрепление изученного материала
Цель деятельности	Деятельность учителя		Деятельность учащихся
Научить применять полученные знания при решении задач	(Ф/И) Организует деятельность учащихся. 1. Решить задачи № 271, 275 на доске и в тетрадях. 2. Решить задачу № 278. 3. Решить задачи № 281, 282 по готовым чертежам (устно)		№ 271. Дано:АВа, АС – наклонная, АВ + АС = 17 см, АС – АВ = 1 см. Найти:АВ. 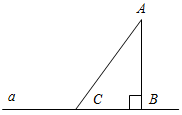Рис. 4 Решение: 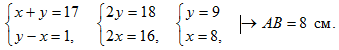Ответ: 8 см. № 275. Дано:АВС, АС = СВ, МАВ, МЕАС, MKВС, МЕ = MK. Доказать:СМ АВ. 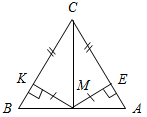Рис. 5 Доказательство: 1) Рассмотрим ВKM и АЕМ. KM = ЕМ (по усл.), В = А (так как АВС – равнобедренный). ВKM = АЕМ (по катету и острому углу), тогда ВМ = МА (по определению равных треугольников). 2) Так как М – середина АВ, значит, СМ – медиана равнобедренного треугольника, опущенная на основание, тогда СМ АВ. № 278. Дано:АВ || СD, АDС = 30°, АD = 6 см, ВСАВ. Найти: ВС. 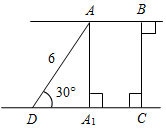Рис. 6 Решение: 1) Рассмотрим АА1D: А1 = 90°, D = 30°, так как АА1 лежит против угла 30°, то АА1 = АD, АА1 = 3 см. 2) Так как АА1 = ВС, то ВС = 3 см. Ответ: 3 см
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Что называется перпендикуляром, наклонной, расстоянием от точки до прямой, расстоянием между параллельными прямыми? – Составьте синквейн к уроку		(И) Домашнее задание: изучить п. 38; ответить на вопросы 14–18 на с. 89 учебника; решить задачи № 272, 277, 283; принести циркули и линейки

1   ...   29   30   31   32   33   34   35   36   ...   47

---

Урок54. Построение треугольника по трем элементам

Цели деятельности учителя	Создать условия для рассмотрения задач на построение треугольника по трем элементам
Термины и понятия	Угол, окружность, дуга окружности, отрезок
Планируемые результаты
Предметные умения		Универсальные учебные действия
Умеют применять изученные понятия, методы для решения задач практического характера		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач; понимают и используют математические средства наглядности. Регулятивные: осуществляют самоконтроль и взаимоконтроль. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задания для групповой работы

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать теоретические знания	(Ф/И) 1. Фронтальный опрос учащихся по изученному ранее материалу. 2. Обсуждение вопросов 14–18 на с. 89. 3. Проверка домашнего задания: двое учащихся на доске решают № 272, 277. № 272. Дано:АВС, АВ = ВС = АС, АD – биссектриса А, DKAС, DK = 6 см. Найти:АD. 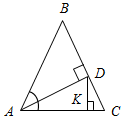Рис. 1 Решение: 1) Так как АВС – равносторонний, то: а) АDВС; б) А = В = С = 60°. 2) Рассмотрим ADK:K = 90°, DAK = 30°, DK = 6 см; так как DK лежит против угла в 30°, то АD = 2DK; АD = 12 см. Ответ: 12 см. № 277. Дано:а || b, АВа, АВ = 3 см, а || с, MN а, MN = 5 см. Найти: расстояние между b и с. 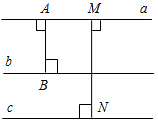Рис. 2 Решение: 1) Так как а || b (по усл.) а || с (по усл.), следовательно, b || с (свойство параллельных прямых). 2) KF = 5 – 3 = 2 см или KF = 5 + 3 = 8 см. 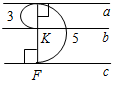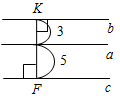Ответ: 2 см или 8 см
II этап. Изучение нового материала
Цель деятельности	Совместная деятельность
Рассмотреть задачи на построение треугольника по трем элементам	(Г) 1. Напомнить учащимся, что значит решить задачу на построение с помощью циркуля и линейки; можно рас-сказать о том, что обычно задачи на построение решаются по схеме, состоящей из четырех частей: 1) анализ; 2) построение; 3) доказательство; 4) исследование (описание схемы содержится в пункте «Задачи повышенной трудности к главам III и IV» на с. 93 учебника). 2. Продолжить работу в группах. При выполнении задания учащиеся могут общаться друг с другом, обсуждать решение задачи. 1-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = PQ, A = М, В = N. 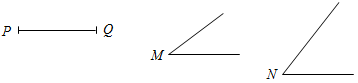Рис. 3 2-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = MN, AC = RS, A = Q. 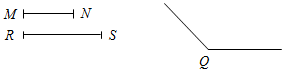Рис. 4 3-я группа С помощью циркуля и линейки без делений построить ∆АВС такой, что АВ = MN, ВС = PQ, AC = RS. 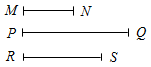Рис. 5 Когда группы будут готовы, заслушать решение каждой задачи, обсудить правильность решения. 3. Обсудить общий вопрос для всех групп: – Всегда ли можно построить такой ∆АВС, который удовлетворял бы всем условиям задачи? 4. Решить в тетради задачи (самостоятельно). 1) Построение треугольника по стороне и прилежащим к ней углам. 2) Построение треугольника по двум сторонам и углу между ними. 3) Построение треугольника по трем сторонам
III этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
Совершенствовать навыки решения задач на построение	(Ф/И) Организует деятельность учащихся. 1. Решить задачу № 286. 2. Решить задачу № 284 (рис. 142)(решение приведено в учебнике на с. 86)	№ 286. Дано: Построить:АВС: АВ = а, А = , АD = l. Анализ: 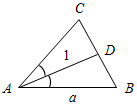Рис. 6 Ход построения: 1) отрезок АВ = а; 2) угол А = ; 3) биссектриса АD = l; 4) соединить В и D прямой; 5) ВD сторону угла А в точке С; 6) АВС – искомый
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Что повторили на уроке? Что нового узнали? – Оцените свою работу и работу группы		(И) Домашнее задание: изучить п. 39 (1 и 2); решить задачи № 274, 285

---