Файл: Урок Прямая и отрезок.docx

Урок55. Решение задач

Цели деятельности учителя	Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки
Термины и понятия	Угол, окружность, дуга окружности, отрезок
Планируемые результаты
Предметные умения		Универсальные учебные действия
Имеют систематические знания о плоских фигурах и их свойствах, владеют умением применять систематические знания о них для решения геометрических и практических задач		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: умеют осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем, аргументировать и отстаивать свою точку зрения. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Чертежи к задачам

1   ...   30   31   32   33   34   35   36   37   ...   47

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Деятельность учителя		Деятельность учащихся
Систематизировать полученные знания	(Ф/И) 1. Ответить на вопросы учащихся по выполнению домашнего задания. 2. Организовать решение задач № 285, 291 (д) с последующим обсуждением (дать учащимся на каждую задачу 2–3 минуты; решение записывается в тетрадях и на доске)		№ 285. Построение: 1) Построим прямую l, перпендикулярную прямой b и проходящую через произвольную точку X прямой b. 2) Отложим от точки X на прямой l отрезок XY, равный PQ. 3) Построим прямую с, перпендикулярную прямой l и проходящую через точку Y. 4) Точку пересечения а и с обозначим А. Точка А прямой а удалена от прямой b на расстояние PQ, то есть А – искомая точка. Задача имеет два решения: отрезок XY на прямой l можно отложить в разные стороны от прямой b. 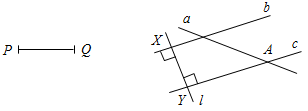Рис. 1 № 291 (д). Дано: медиана PQ, проведенная к основанию; основание равнобедренного треугольника ST. Построение: Так как медиана, проведенная к основанию равнобедренного треугольника, является его высотой, то ход построения будет следующим: 1) На прямой а отложим отрезок АВ, равный ST. 2) Построим середину отрезка АВ – точку М. 3) Через точку М построим прямую b, перпендикулярную прямой а, и отложим на этой прямой b от точки М отрезок MC, равный PQ. 4) Соединим точки А и С, В и С отрезками. ∆АВС – искомый. Задача имеет два решения: на прямой b от точки М можно отложить два отрезка, равных PQ. 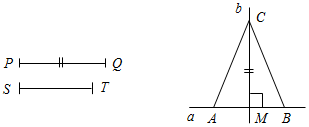Рис. 2
II этап. Учебно-познавательная деятельность
Цель деятельности	Совместная деятельность
Изучить новый мате- риал	(Ф/И) 1. Разобрать решение задачи № 3 на доске и в тетрадях (с. 84–85). 2. Построить треугольник по трем сторонам (рис. 141 и решение задачи на с. 85 учебника). Провести исследование, всегда ли задача № 3 имеет решение
III этап. Решение задач
Цель деятельности	Деятельность учителя		Деятельность учащихся
Совершенствовать навыки в решении задач	(Ф/И) Организует деятельность учащихся: решение задач № 289, 290, 292 на доске и в тетрадях		№ 289. Дано: ПостроитьАВС: АВ = PQ, А = hk, В = h1k1. Ан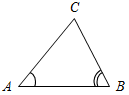ализ: Ход построения: 1) Отрезок АВ = PQ; 2) А =hk; 3) В = h1k1; 4) стороны А и В пересекаются в точке С; 5) АВС – искомый. № 290. а) Дано: ПостроитьАВС: С = 90°, АС = а, СВ = b. Анализ: 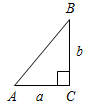Ход построения: 1) Построить прямой угол С; 2) на одной стороне отложить отрезок АС = а, а на другой – СВ = b; 3) соединить отрезком А и В; 4) АВС – искомый. б) Дано: ПостроитьАВС: С = 90°, А = , АС = а. Анализ: 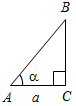Ход построения: 1) Построить прямой угол С; 2) отложить на стороне угла АС = а; 3) построить А = ; 4) стороны А и С пересекаются в точке В; 5) АВС – искомый. № 292. Дано: а) ПостроитьАВС: АВ = P1Q1, ВС = P2Q2, АС = 2P3Q3. Анализ: 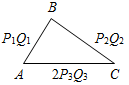Ход построения: 1) Отрезок АВ = P1Q1; 2) окружность с центром А и R = P2Q2; 3) окружность с центром В и R = 2P3Q3; 4) эти две окружности пересекаются в точке С; 5) АВС – искомый. б) ПостроитьАВС: АВ = 2P1Q1, ВС = P2Q2, АС = P3Q3. Ан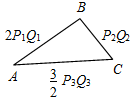ализ: Ход построения: 1) ВС = P2Q2; 2) окружность с центром В и R = 2P1Q1; 3) окружность с центром С и R = P3Q3; 4) окружности пересекаются в точке А; 5) АВС – искомый. Указание: нужно помнить, что сумма длин двух сторон треугольника должна быть больше длины третьей стороны
IV этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Оцените свою работу на уроке. – Закончите фразы: • Я познакомился с... • Было непросто... • Я добился... • У меня получилось... • Хотелось бы... • Мне запомнилось... • Я попробую...		(И) Домашнее задание: пункты 38–39; вопросы 14–20 на с. 89; решить задачи № 273, 287, 288, 291 (а, б, г), 293 (разобрана в учебнике на с. 87–88)

---

Урок56. Решение задач

Цель деятельности учителя	Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки
Термины и понятия	Угол, окружность, дуга окружности, отрезок, искомый треугольник
Планируемые результаты
Предметные умения		Универсальные учебные действия
Усваивают систематические знания о плоских фигурах и их свойствах, владеют умениями применять систематические знания о них для геометрических и практических задач, решать задачи на построение		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: осуществляют контроль по результату и по способу действия на уровне произвольного внимания и вносят необходимые коррективы. Коммуникативные: умеют работать в сотрудничестве с учителем. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И)
Образовательные ресурсы	• Задания для фронтальной работы. • Задания для самостоятельной работы

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать знания	(Ф/И) 1. Проверить выполнение домашней работы. 2. Решить задачи. 1) В треугольнике ABCС = 30°, АС = 10 см, ВС = 8 см. Через вершину А проведена прямая а, параллельная ВС. Найдите: а) расстояние от точки В до прямой АС; б) расстояние между прямыми а и ВС. 2) Постройте равносторонний треугольник, у которого сторона в два раза меньше данного отрезка
II этап. Самостоятельная работа
Цель деятельности	Задания для самостоятельной работы
Проверить уровень владения умением решать задачи на построение	(И) Работа выполняется на листках и в конце урока сдается на проверку учителю. Вариант I 1. Постройте прямоугольный треугольник по катету и прилежащему острому углу. 2. Даны отрезки PQ и P1Q1 и угол hk. Постройте треугольник СDЕ так, чтобы СЕ = PQ, С = hk, СF = P1Q1, где СF – высота треугольника. Вариант II 1. Постройте равнобедренный треугольник по основанию и медиане, проведенной к основанию. 2. Даны отрезки PQ, P1Q1 и P2Q2. Постройте треугольник ЕKF так, чтобы ЕF = PQ, KF = P1Q1 и FD = P2Q2, где FD – высота треугольника
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Почему было трудно? – Что открыли, узнали на уроке? – Оправдались ли ваши ожидания от урока? – Что вы взяли с сегодняшнего урока?		(И) Домашнее задание: решить задачи № 294, 295

---

Урок57. Решение задач

Цели деятельности учителя	Создать условия для обучения учащихся решению задач на построение с помощью циркуля и линейки, для подготовки к контрольной работе
Термины и понятия	Угол, окружность, дуга окружности, отрезок, искомый треугольник
Планируемые результаты
Предметные умения		Универсальные учебные действия
Закрепляют систематические знания о плоских фигурах и их свойствах; владеют умениями применять систематические знания о них для геометрических и практических задач, решать задачи на построение		Познавательные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач. Регулятивные: осуществляют контроль по результату и по способу действия на уровне произвольного внимания и вносят необходимые коррективы; умеют контролировать процесс и результат учебной математической деятельности. Коммуникативные: умеют работать в сотрудничестве с учителем, в группе. Личностные: осознают важность и необходимость изучения предмета
Организация пространства
Формы работы	Фронтальная (Ф); индивидуальная (И); групповая (Г)
Образовательные ресурсы	• Задание для фронтальной работы

1   ...   31   32   33   34   35   36   37   38   ...   47

---

I этап. Актуализация опорных знаний учащихся
Цель деятельности	Совместная деятельность
Систематизировать знания	(Ф/И) 1. Проверить выполнение домашнего задания. Для этого вызвать к доске двоих учащихся. № 294. Дано: ПостроитьАВС: АВ = b, АС = а, CD = c, CDAB. Анализ: 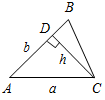Ход построения: 1) Прямой угол D; 2) на одной стороне отложить отрезок DC = h; 3) окружность с центром в точке C и R = а; 4) окружность пересечет другую сторону прямого D в точке А; 5) отложить АВ = b; 6) АВС – искомый. № 295. Дано: Построить АВС. Анализ: 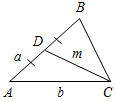Ход построения: 1) Отрезок АВ = а; 2) середина АВ – точка D; 3) окружность с центром в точке D и R = т и окружность с центром в точке А и R1 = b; 4) окружности пересекаются в точке С; 5) соединить отрезком точки В и С; 6) АВС – искомый. 2. Сообщить результаты самостоятельной работы
II этап. Решение задач
Цель деятельности	Деятельность учителя	Деятельность учащихся
Совершенствовать навыки решения задач	(Г) Организует деятельность учащихся. 1. Решить задачи по группам: № 301, 302, 308, 315, 316 (можно предложить группам самим выбрать задачу). (Ф/И) 2. Построить прямоугольный треугольник по гипотенузе и внешнему углу при вершине острого угла. Решение: Начертим данные отрезок PQ и угол hk. 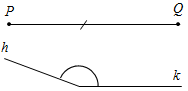Рис. 1 Построение: 1) Проведем прямую, отметим на ней точку В и отложим отрезок ВС, равный PQ. 2) Отложим от луча ВD, являющегося продолжением луча ВС, угол DВМ, равный углу hk. 3) Построим прямую, проходящую через точку С и перпендикулярную к прямой ВМ, и обозначим буквой А точку пересечения этой прямой с лучом ВМ. Треугольник АВС – искомый. 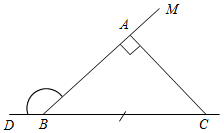Рис. 2 Доказательство (устно): По построению треугольник АВС – прямоугольный, гипотенуза ВС равна данному отрезку РQ и внешний угол АВD треугольника равен данному углу hk. Таким образом, построенный треугольник АВС удовлетворяет всем условиям задачи. Указание:задача имеет решение только в том случае, когда данный угол hkтупой. Желательно, чтобы учащиеся сами обосновали справедливость этого утверждения	№ 301. Дано: АНа, АМ1, АМ2 – наклонные. а) Доказать:АМ1 = АМ2, если НМ1 = НМ2. 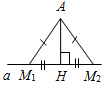Рис. 3 Рассмотрим АНМ1 и АНМ2: АН – общая, НМ1 = НМ2 (по усл.), АНМ1 = = АНМ2 (по катетам), тогда АМ1 = АМ2, что и требовалось доказать. б) Доказать: АМ1<АМ2, если НМ1<НМ2. 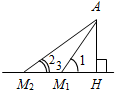Рис. 4 1) В АНМ1: Н = 90°, значит, 1 – острый. 2) ВАНМ2: Н = 90°, значит, 2 – острый. 3) В АМ1М2: 2 – острый, 3 – тупой (как смежный с острым), значит АМ2>АМ1, что и требовалось доказать. № 302. Дано: АНа, АМ1, АМ2 – наклонные. а) Доказать:НМ1 = НМ2, если АМ1 = АМ2. 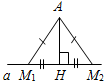Рис. 5 Рассмотрим АНМ1 и АНМ2: АН – общая, АМ1 = АМ2 (по усл.), АНМ1 = = АНМ2 (по катету и гипотенузе), тогда НМ1 = НМ2. б) Доказать:НМ1<НМ2, если АМ1<АМ2. 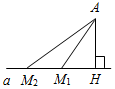Рис. 6 1) Примем НМ1 не <НМ2, то есть НМ1>НМ2 или НМ1 = НМ2. 2) Если НМ1 = НМ2, то получим результат аналогично 301 (а), что противоречит условию АМ1<АМ2, значит, предположение НМ1 = НМ2 неверно. 3) Если НМ1>НМ2, то, по 301 (б), получим АМ1>АМ2, значит, предположение НМ1>НМ2 неверно. Вывод: НМ1<НМ2. № 308. Дано:АВС – равнобедренный, АС = 37 см – основание, внешний угол при вершине В равен 60°. Найти: расстояние от вершины С до прямой АВ. 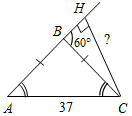Рис. 7 Решение: 1) АВС – равнобедренный; по задаче 232, 2А = 60°, следовательно, А = 30°. 2) СНА – прямоугольный (по условию), А = 30°, следовательно, по свойству, СН = АС, СН = 37 : 2 = 18,5 см. № 315. Построить при помощи циркуля и линейки угол, равный: а) 30°; б) 60°; в) 15°; г) 120°; д) 150°; е) 135°; ж) 75°; и) 105. 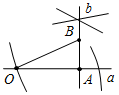Рис. 8 а) Ход построения: 1) Возьмем произвольную прямую а и произвольную точку Аа; 2) строим прямую b так, чтобы Аb и аb (по задаче о построении перпендикулярных прямых); 3) находим точку В, чтобы Вb и АВ – произвольной длины; 4) строим окружность w с центром в точке В и радиусом, равным 2АВ; 5) окружность w пересекает прямую а в точке О; 6) АВС – искомый. Доказательство: АОВ – прямоугольный (по построению) и АВ = ОВ (по построению), следовательно, по свойству, АОВ = 30°. б) Угол в 60° построен в п. а) одновременно с углом в 30° (это ОВА). в) Построенный в п. а) угол в 30° следует разделить пополам (по задаче о построении биссектрисы угла). г) Поскольку 120° = 180° – 60°, этот угол построен в п. а) – это угол, смежный АВО. д) Поскольку 150° = 180° – 30°, этот угол построен в п. а) – это угол, смежный АОВ. е) Поскольку 135° = 90° + 45°, следует построить две перпендикулярных прямых и один из полученных прямых углов разделить пополам (по задаче о построении биссектрисы угла). ж) Поскольку 165° = 180° – 15°, это угол, смежный построенному в п. в). Необходимо построить перпендикуляр к одной из сторон построенного угла, проходящий через его вершину. Один из полученных углов составит 75°. и) Поскольку 105° = 90° + 15°, это другой из углов, полученных в п. ж). № 316. Дано:P1Q1 – сторона, P2Q2 – высота к P1Q1, P3Q3 – медиана. Построить:АВС (СН = P2Q2, АМ = P3Q3, АВ = P1Q1). Ход построения: Строим две параллельные прямые, расположенные друг от друга на расстоянии, равном данной высоте треугольника. На одной из прямых отмечаем точку А и откладываем отрезок АВ, равный данной стороне треугольника. Строим окружность с центром А и радиусом, вдвое большим данной медианы треугольника. Строим середину М отрезка AD, где D – точка пересечения окружности и второй прямой, и проводим прямую ВМ до пересечения со второй из параллельных прямых в точке С. АВС – искомый 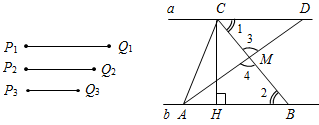Рис. 11
III этап. Итоги урока. Рефлексия
Деятельность учителя		Деятельность учащихся
(Ф/И) – Обычно мы заканчиваем урок, оценивая свою работу и работу товарищей. Объективно оценить себя – самое сложное. Об этом сказал А. де Сент-Экзюпери: «Суди себя сам. Это самое трудное. Себя судить куда труднее, чем других. Если ты сумеешь правильно судить себя, значит, ты поистине мудр»		(И) Домашнее задание: решить задачи № 314, 317; подготовиться к контрольной работе

---