Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4596
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
2 = −5 −3i.
4. Вычислить n-ю степень некоторого комплексного числа z= -2-3⋅i где n=2
5.Построить график функции y=2∗2х+3 и найти множество значений.
6.Изобразить схематически график функции у=log3Х+3 и найти производную в точке х=1.
7.Найти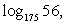 если
если 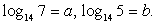
8. Решить уравнение
9 х − 6 · 3 х − 27 = 0.
9. Решить неравенство:log2(3−x)<−1.
2 ВАРИАНТ
1.Выполнить действия над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1-Z2
если
Z1 = (3 – 2i), Z2 = (5 + 3i)
2.Решить уравнение:
x2 – 4x + 13 = 0.
3. Изобразить на плоскости числа :z1 = 2 + 3i и z2 = −1 + 4i
4.Вычислить n-ю степень некоторого комплексного числа z=2+3⋅i
где n=3
5.Построить график функции у =2∗2х-3 и найти множество значений.
6.Изобразить схематически график функции у=log2Х-3 и найти производную в точке х=1.
.7.Вычислить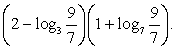
8. Решить уравнение : 100х − 11 · 10х + 10 = 0
9.Решить неравенство log0,5(x−2)≥log0,5(2x−12).
3 ВАРИАНТ
1.Выполнить действия над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1+Z2
Z1 = (4 + 2i), Z2 = (– 3 + 2i).
2.Решить уравнение:
x2 + 3x + 4=0
3. Изобразить на плоскости числа:
Z1= - 4 +3i Z2= - 2 -5i
4.Вычислить n-ю степень некоторого комплексного числа z=2- i
где n=5.
5.Построить график функции y=2∗3х-1 и найти множество значений.
6.Изобразить схематически график функции у=log2Х+3 и найти производную в точке х=2.
7.Найдите log308, если lg 5 = а и lg 3 = b.
8. Решить уравнение :
4 х + 2x+1 − 8 = 0;
9.Решить неравенство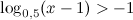
4 ВАРИАНТ
1.Выполнить действие над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1-Z2
Z1 = (– 2 + 3i), Z2 = (7 – 2i)
2.Решить уравнение:
2,5x2 + x + 1 = 0..
3.Изобразить на плоскости числа:
z
1 = 2 − 3i и z2 = 1 + 2i
4.Вычислить n-ю степень некоторого комплексного числа z=-3+2⋅i
где n=4
5.Построить график функции y=2∗3х+1 и найти множество значений.
6.Построить схематически график функции у=log5Х+3 и найти производную в точке х=3.
Схема выставления баллов
1 вариант
4. Вычислить n-ю степень некоторого комплексного числа z= -2-3⋅i где n=2
5.Построить график функции y=2∗2х+3 и найти множество значений.
6.Изобразить схематически график функции у=log3Х+3 и найти производную в точке х=1.
7.Найти
8. Решить уравнение
9 х − 6 · 3 х − 27 = 0.
9. Решить неравенство:log2(3−x)<−1.
2 ВАРИАНТ
| Оценивание заданий работы | |||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество баллов | 3 | 2 | 2 | 1 | 2 | 2 | 3 | 5 | 2 |
| Всего баллов | 22 балла | ||||||||
1.Выполнить действия над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1-Z2
если
Z1 = (3 – 2i), Z2 = (5 + 3i)
2.Решить уравнение:
x2 – 4x + 13 = 0.
3. Изобразить на плоскости числа :z1 = 2 + 3i и z2 = −1 + 4i
4.Вычислить n-ю степень некоторого комплексного числа z=2+3⋅i
где n=3
5.Построить график функции у =2∗2х-3 и найти множество значений.
6.Изобразить схематически график функции у=log2Х-3 и найти производную в точке х=1.
.7.Вычислить
8. Решить уравнение : 100х − 11 · 10х + 10 = 0
9.Решить неравенство log0,5(x−2)≥log0,5(2x−12).
3 ВАРИАНТ
| Оценивание заданий работы | |||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество баллов | 3 | 2 | 2 | 1 | 2 | 2 | 3 | 5 | 2 |
| Всего баллов | 22 балла | ||||||||
1.Выполнить действия над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1+Z2
Z1 = (4 + 2i), Z2 = (– 3 + 2i).
2.Решить уравнение:
x2 + 3x + 4=0
3. Изобразить на плоскости числа:
Z1= - 4 +3i Z2= - 2 -5i
4.Вычислить n-ю степень некоторого комплексного числа z=2- i
где n=5.
5.Построить график функции y=2∗3х-1 и найти множество значений.
6.Изобразить схематически график функции у=log2Х+3 и найти производную в точке х=2.
7.Найдите log308, если lg 5 = а и lg 3 = b.
8. Решить уравнение :
4 х + 2x+1 − 8 = 0;
9.Решить неравенство
4 ВАРИАНТ
| Оценивание заданий работы | |||||||||
| № задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Количество баллов | 3 | 2 | 2 | 1 | 2 | 2 | 3 | 5 | 2 |
| Всего баллов | 22 балла | ||||||||
1.Выполнить действие над комплексными числами, найти модуль и сопряженное число полученного результата:
Z1-Z2
Z1 = (– 2 + 3i), Z2 = (7 – 2i)
2.Решить уравнение:
2,5x2 + x + 1 = 0..
3.Изобразить на плоскости числа:
z
1 = 2 − 3i и z2 = 1 + 2i
4.Вычислить n-ю степень некоторого комплексного числа z=-3+2⋅i
где n=4
5.Построить график функции y=2∗3х+1 и найти множество значений.
6.Построить схематически график функции у=log5Х+3 и найти производную в точке х=3.
Схема выставления баллов
1 вариант
| № | Ответ | Балл | Альтернативный ответ | |
| 1 | Z1+Z2 =3+5i+7-2i=(3+7)+i(5-2)=10+3i | 1 | | |
| 10+3i ,ему сопряженное 10-3i | 1 | | ||
| | 1 | | ||
| 2 | D1=100-4*26=-4 | 1 | | |
| Х1.2 | 1 | | ||
| 3 | 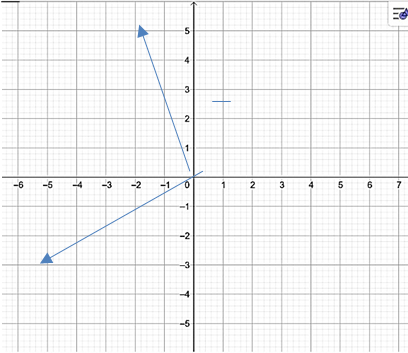 | 1 | | |
| 4 | (-2- 3i)2 = (-2)2 - 2·(-2)·3i + (-3i)2 = 4 +12i + 9·(-1) = -5+12i | 1 | | |
| 5 | 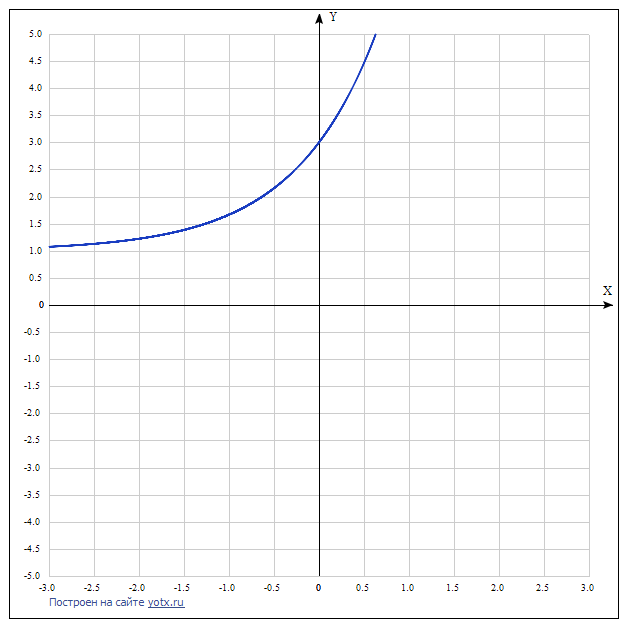 | 1 | | |
| y>3 | 1 | | ||
| 6 | 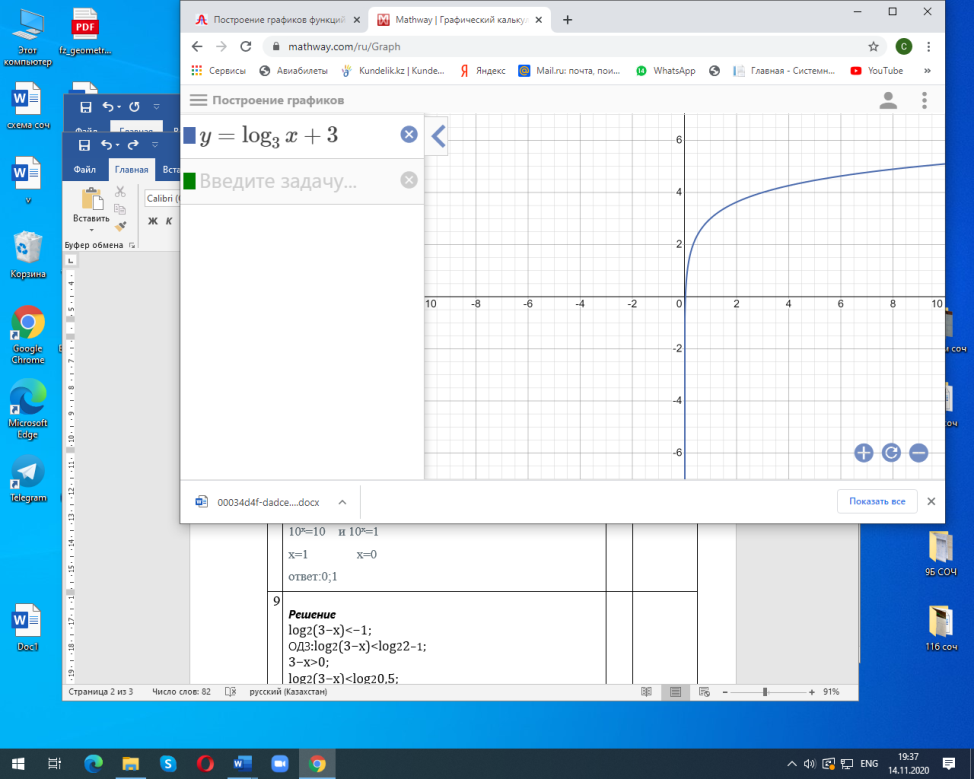 | 1 | | |
| y/= | 1 | | ||
| 7 | | 1 | | |
| | = | 1 | | |
| | = | 1 | | |
| | | 1 | | |
| | = | 1 | | |
| 8 | 10x=у,у2-11у+10=0 | 1 | | |
| D=112-4*1*10=81 | 1 | | ||
| У1,2= | 1 | | ||
| 10х=10 и 10х=1 х=1 х=0 | 1 | | ||
| ответ:0;1 | 1 | | ||
| 9 | Log2(3−x)<−1; ОДЗ:log2(3−x) 3−x>0; −x>−3; x<3; x∈(−∞;3). | 1 | | |
| log2(3−x) 3−x<0,5; −x<0,5−3; −x<−2,5; x>2,5; x∈(2,5;+∞); | 1 | | ||
| {x∈(2,5;+∞)x∈(−∞;3)
| 1 | | ||
| |