Файл: Сборник работ для суммативного оценивания по алгебре и началам анализа 11 класс.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 29.11.2023
Просмотров: 4598
Скачиваний: 247
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «СТЕПЕНИ И КОРНИ. СТЕПЕННАЯ ФУНКЦИЯ»
РУБРИКА ДЛЯ ПРЕДОСТАВЛЕНИЯ ИНФОРМАЦИИ РОДИТЕЛЯМ
ПО ИТОГАМ СУММАТИВНОГО ОЦЕНИВАНИЯ
ЗА РАЗДЕЛ «ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА»
Ответ: x∈(2,5;3).
Решение.
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания
Продолжительность – 40 минут
Количество баллов – 25
Типы заданий:
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 3 заданий, включающих вопросы с развернутым ответом.
Разрешается использование калькулятора.
Характеристика заданий суммативного оценивания за 4 четверть
Задания суммативного оценивания
1 ВАРИАНТ
а) Общее решение дифференциального уравнения
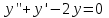
b) частное решение дифференциального уравнения пункта (а), учитывая следующие условия: у(0) =2, у’=2, x=0
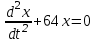
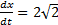
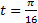
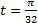
b) x=4 при
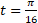
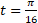 , а
, а 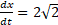
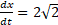 при
при 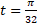
| 1 1 1 1 1 1 | | ||||||||||||||||||
| | 4 вариант | | | ||||||||||||||||
| 1 | Z1-Z2 =(2-3i)-(1+2i)=(2-1)+i(-3-2)=1+5i 1+5i ,ему сопряженное 1-5i | 1 1 1 | | ||||||||||||||||
| 2 | D=1-4*2,5= -9 Х1.2 | 1 1 | | ||||||||||||||||
| 3 |  | 1 1 | | ||||||||||||||||
| 4 | (-3+2i)4 = (2i-3)4=16i4-4*8i3*3-6*4i2*9-4*2i*27+81=16i+96i-216-216+81= =-341+112i | 1 | | ||||||||||||||||
| 5 | 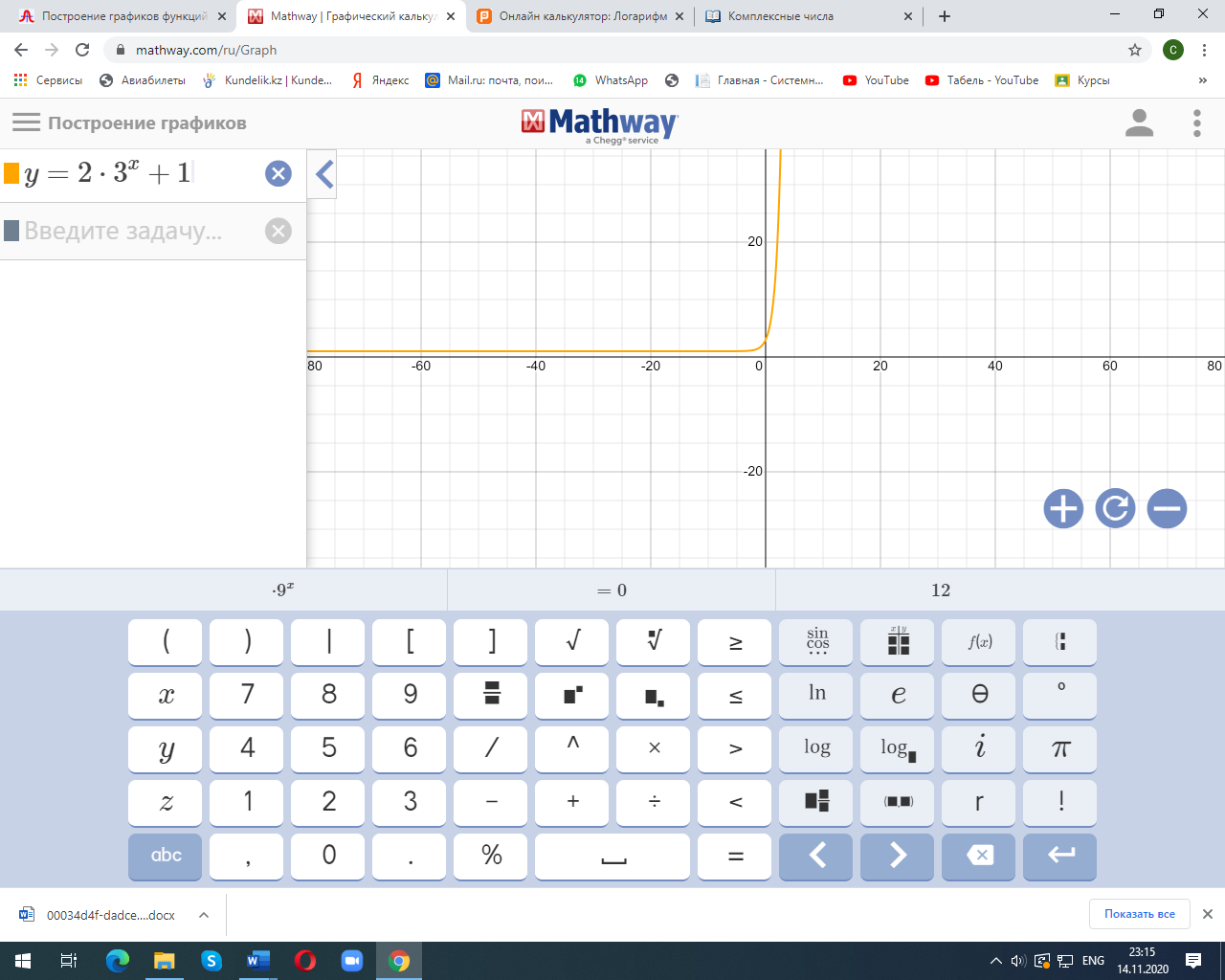 y>1 | 1 1 | | ||||||||||||||||
| 6 | 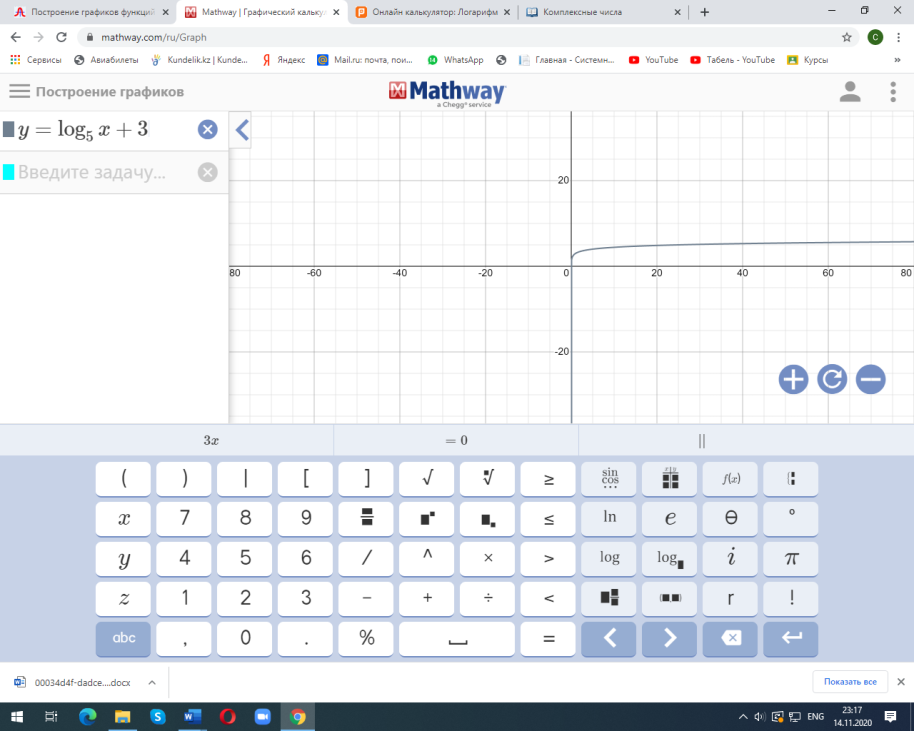 y/= | 1 1 | | ||||||||||||||||
| 7 | | 1 1 1 | | ||||||||||||||||
| 8 | 2x=t,2t2-5t+2=0 D=25-4*2*2=9 t1,2= 2x=2 2x= x=1 x=-1 ответ :-1;1. | 1 1 1 1 1 1 | | ||||||||||||||||
| 9 | log3(x2 - x) ≥ log3(x + 8) ⇔
Ответ: x ∈ (-8;-2]∪[4;+∞). | 1 1 1 1 1 1 | |
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ
Обзор суммативного оценивания
Продолжительность – 40 минут
Количество баллов – 25
Типы заданий:
РО – задания, требующие развернутого ответа.
Структура суммативного оценивания
Данный вариант состоит из 3 заданий, включающих вопросы с развернутым ответом.
-
вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов.
Разрешается использование калькулятора.
Характеристика заданий суммативного оценивания за 4 четверть
| Раздел | Проверяемая цель | Уровень мыслительных навыков | Кол. заданий* | № задания* | Тип задании я* | Время на выполнение, мин* | Балл* | Балл за раздел |
| Дифференциальные уравнения | 11.4.1.25 - решать линейные однородные дифференциальные уравнения второго порядка (вида ay''+by'+cy=0 , где a,b,c - постоянные) 11.4.1.23 - знать определения частного и общего решений дифференциального уравнения | Применение | 1 | 1 | РО | 10 | 8 | |
| знание и применение | ||||||||
| 11.4.1.22 - знать основные понятия о дифференциальные уравнения | знание и понимание | 1 | 2 | РО | 15 | 7 | | |
| 11.4.3.1-применять дифференциальные уравнения при решении физических задач | навыки высокого порядка | |||||||
| 11.4.1.24- решать дифференциальные уравнения с разделяющимися переменными | применение | |||||||
| 11.4.3.2- составлять и решать уравнение гармонического колебания | навыки высокого порядка | 1 | 3 | РО | 15 | 10 | | |
| ИТОГО: | | | 3 | | | 40 | 25 | 25 |
| Примечание: * - разделы, в которые можно вносить изменения | ||||||||
Задания суммативного оценивания
1 ВАРИАНТ
| Оценивание заданий работы | |||
| № задания | 1 | 2 | 3 |
| Количество баллов | 8 | 7 | 10 |
| Всего баллов | 25 балла | ||
-
Найдите:
а) Общее решение дифференциального уравнения
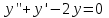
b) частное решение дифференциального уравнения пункта (а), учитывая следующие условия: у(0) =2, у’=2, x=0
-
Если температура воздуха равна 20° С и тело в течение 20 мин охлаждается от 100° С до 60° С, то
-
Запишите общее уравнение охлаждения тела по заданным условиям. -
через сколько времени его температура понизится до 30° С?
-
Частица совершает простое гармоническое движение. Отклонение от центра колебания частицы равно x метрам за время t секунд.
-
Покажите, что x = Acos8t + Bsin8t является общим решением дифференциального уравнения
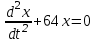
b) x=4 при