Файл: Курсовой проект по Детали машин и основы конструирования наименование дисциплины.docx

Для колеса:
σ_Hlim2 =1,8 248,5+67=514 H/мм²
σ_Flim2 =1,03 248,5=256 H/мм²
Для шестерни:
σ_Hlim1=1,8 285,5+67=581 H/мм²
σ_Flim1=1,03 285,5=294 H/мм²
где σ_Hlim и σ_Flim – пределы выносливости.

Допускаемы контактные и изгибные напряжения получают умножением значений σ_Hlim и σ_Flim на коэффициенты Z_N и Y_N. Из ранее выполненных расчетов видно, что все коэффициенты Z_N и Y_N = 1. Поэтому допускаемые контактные и изгибные напряжения:

[σ]H= σHlim

(2.7)

[σ]F= σFlim

(2.8)

Таким образом:
[σ]_H = 514 Н/мм²;
[σ]_F2 = 256 Н/мм²;
[σ]_F1 = 294 Н/мм².

2.6 Проектный расчет передачи

Определяем межосевое расстояние по формуле (с.21 [1]):

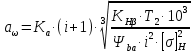(2.9)

где K_a - коэффициент межосевого расстояния; для косозубых передач K_a =43; стр 20 [1];

i - передаточное отношение передачи;

Т₂ - вращающий момент на валу колеса (по заданию значение берем с третьего вала), Н·м;

K_Hβ- коэффициент неравномерности распределения нагрузки по длине зуба. Для мягких материалов K_Hβ = 1; стр 60 [1]

_ba - коэффициент ширины венца колеса;

[]_H - допускаемое контактное напряжение колеса с менее прочным зубом или среднее допускаемое контактное напряжение.

Принимаем _ba =0,3; стр 60 [2]

Подставляя все значения в формулу 2.9 получаем:

---

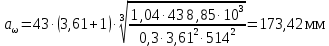
Полученное значение межосевого расстояния a_ω округляют в большую сторону до стандартного по СТ СЭВ 310-76: 40, 50, 63, 71, 80, 90, 100, 112, 125, 140, 160, 180, 200, 220, 250, 280, 315 мм.

Принимаем межосевое расстояние равным, (табл.19.1) [1]:

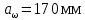
Определяем модуль зацепления.

Выбирают модуль в интервале

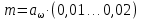(2.10)

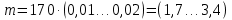
Модуль принимаем из стандартного ряда равным:

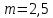
Определяем суммарное число зубьев по формуле (c 22) [1]:

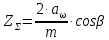(2.11)

где a_ω межосевое расстояние, мм;

m - модуль передачи, мм;

cosβ - угол наклона зубьев, для косозубой β=8÷18.

Принимаем .

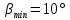Получившееся значение округляем в меньшую сторону.

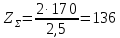
Принимаем
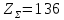
Определяем число зубьев шестерни по формуле (c 22) [1]:

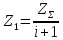(2.12)

где i — передаточное число промежуточной передачи.

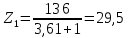
Принимаем число зубьев шестерни равным:

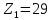
Определяем число зубьев колеса по формуле (c 23) [1]:

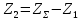(2.13)

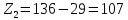
Уточняем фактическое передаточное отношение по формуле (с 23 [1]):

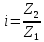(2.14)

---

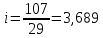
Уточняем угол наклона зуба по формуле (стр 22 [1])

Определяем размеры зубчатых колес.

Делительный диаметр шестерни рассчитываем по формуле (c 23 [1]):

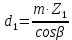(2.15)

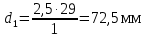
Делительные диаметры колеса по формуле (c 23) [1]:

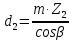(2.16)

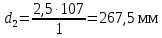
Диаметры окружности впадин зубьев шестерни(c 23) [1]:

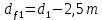(2.17)

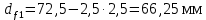
Диаметры окружности впадин зубьев колеса(c 23) [1]:

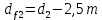(2.18)

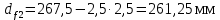
Диаметры окружности вершин зубьев шестерни(c 23) [1]:

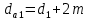(2.19)

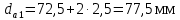
Диаметры окружности вершин зубьев колеса (c 23) [1]:

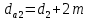(2.20)

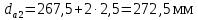
Определяем ширину шестерни и колеса.

Ширину колеса находим по формуле (с.39 [1])

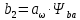(2.21)

---

где _ba - коэффициент ширины венца колеса, принимаем _ba =0,3 (с 20 [1])

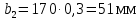
Принимаем ширину колеса равную:

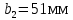
Определяем ширину шестерни по формуле:

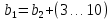(2.22)

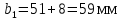
2.7 Проверка зубьев колес по напряжениям изгиба

Определяем силы в зацеплении.

Окружная сила направлена по касательной в точки касания колеса и шестерни и определяется по формуле:

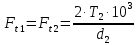(2.23)

где Т₂ - вращающий момент на 2 промежуточном валу, Н·м;

d₂ — делительный диаметр шестерни, мм.

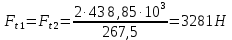
Радиальная сила направлена к центру окружности и определяется по формуле:

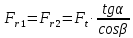(2.25)

где F_t - окружная сила, Н;

α – угол между геометрической суммой радиальной и осевой силами, α = 20;

β - угол наклона зубьев, β =0.

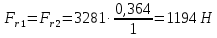
Осевая сила направлена вдоль оси и находится по формуле:

(2.26)

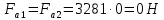
Проверяем зубья колес по напряжениям изгиба. Должно выполняться неравенство:

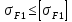(2.27)

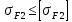(2.28)

---

Определяем напряжение на изгиб зуба колеса по формуле (c 26) [1]:

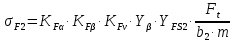(2.29)

где K_Fα - коэффициент, учитывающий распределение нагрузки между зубьями, K_Fα= 1; (c 25 [1]);

K_Fv - коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи, K_Fv = 1,2; (c 26 [1]);

K_Fβ - коэффициент неравномерности нагрузки по длине зуба, K_Fβ = 1;

Y_β - коэффициент, учитывающий наклон зуба Y_β = 0,88 (с 25 [1]);

b2—ширина колеса, мм;

Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжений, Y_FS = 3,61 (таб 2.5 [1]).

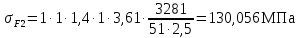
Так как [σ]_F2=256 МПа и σ_F2=130,056 МПа, что удовлетворяет условию [σ]_F2 σ_F2 , то колесо прошло проверку по напряжениям на изгиб.
2.8 Проверка зубьев колес по напряжениям на контакт

Проверяем зубья колес по напряжениям контакта. Расчётное контактное напряжение вычисляется по формуле (c 27 [1]):

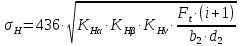(2.30)

где K_H, K_H, K_HV - коэффициенты учитывающие распределение нагрузки между зубьями, неравномерность распределения нагрузки по длине контактной линии, дополнительные динамические нагрузки, так как редуктор рассчитан на долгий срок службы то K_H =1, K_H=1, K_HV =1,1 (стр 27[1]).


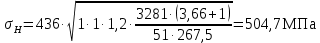
Допускаем 10% перегруза и 5% недогруза (стр 27 [1]).


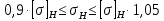
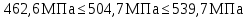
Так как [σ]_H=514 МПа, то колеса прошли проверку по напряжениям на изгиб.

---