Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 292
Скачиваний: 2
СОДЕРЖАНИЕ
1. Основные понятия и определения
3. Дифференциальные уравнения ипередаточные функции
5. Типовые звенья САУ и их характеристики
6. Построение передаточных функций САУ
7. Составление исходных дифференциальныхуравнений САУ
9. Процесс управления и требования к нему
9.1. Оценка устойчивости линейной САУ
9.3. Качество переходного процесса
10.2. Типы корректирующих устройств
10.3. Пример синтеза последовательного корректирующего устройства
10.4. Пример синтеза параллельного корректирующего устройства
11.3. Определение передаточных функций элементов системы
11.4. Построение структурной схемы системы
11.5. Построение логарифмических частотных характеристик разомкнутой системы
11.6. Определение устойчивости и запасаустойчивости по амплитуде и фазе
11.7. Определение критического значения добротностис помощью критерия Гурвица
11.8. Введение скоростной обратной связи
11.9. Нахождение минимального коэффициентаскоростной обратной связи
11.10 Определение оптимального коэффициентаскоростной обратной связи
12.2. Характеристики случайных величин и процессов
12.3. Прохождение случайного сигнала через линейную непрерывную систему
12.4. Расчет установившейся ошибки САУ
12.5. Расчеты по минимуму ошибки
13.1. Общий метод составления уравнений нелинейных САУ
13.3. Устойчивость по Ляпунову
2. Критерий Гурвица.
Составляется матрица из коэффициентов характеристического уравнения следующим образом: по главной диагонали записываются коэффициенты от а1 до аn. Столбцы вверх от главной диагонали заполняются коэффициентами с бóльшими индексами, а вниз – с мéньшими. Там, где коэффициентов нет, ставится 0:
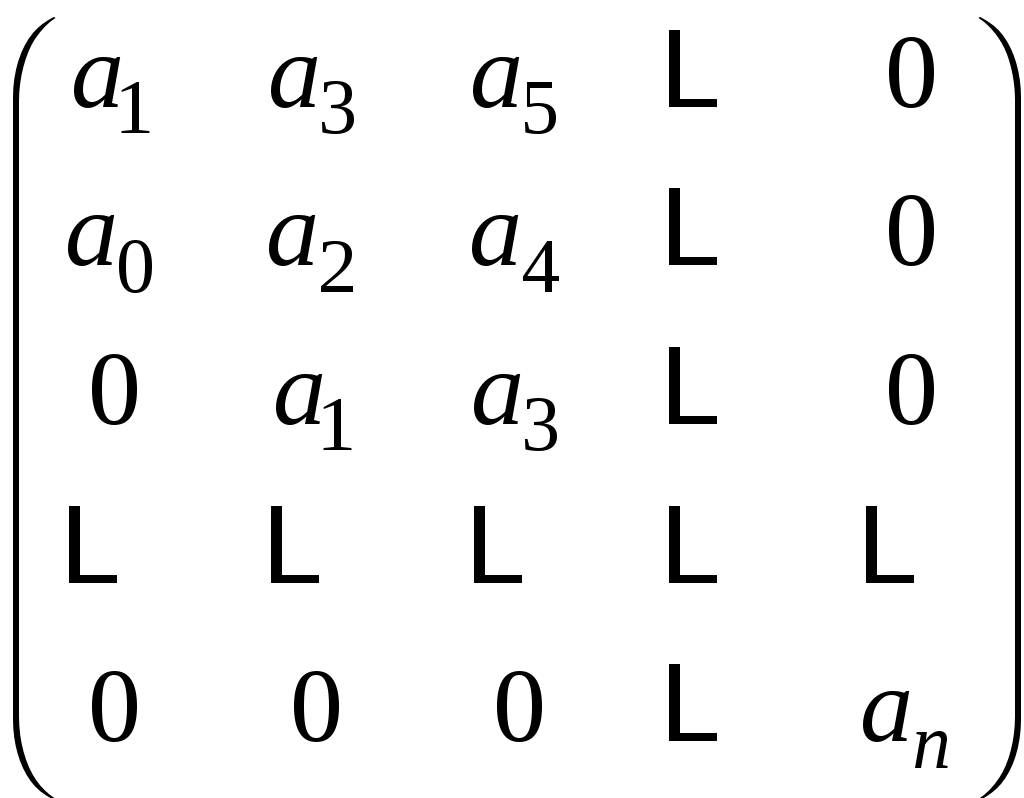 .
.Затем определяются определители данной матрицы.
Критерий формулируется следующим образом: для того, чтобы система была устойчивой, необходимо и достаточно, чтобы все определители были больше нуля при а0 > 0.
Определители вычисляются по формулам:
9.2.2. Частотные критерии устойчивости
1. Критерий устойчивости Михайлова.
Этот критерий основан на анализе годографа характеристического уравнения замкнутой системы.
Линейная система n-го порядка устойчива, если при изменении частоты от 0 до ∞ годограф последовательно обходит n квадрантов комплексной плоскости против часовой стрелки, начинаясь на положительной части вещественной оси, не проходя через начало координат (рис. 33).
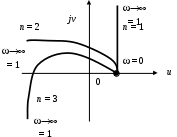
Рис. 33. Годограф Михайлова
Как известно, характеристическое уравнение D(p) САУ равно
Его можно представить как произведение полиномов первого порядка, где pi – корни уравнения
Как известно, для устойчивой системы корень имеет отрицательную вещественную часть.
Рассмотрим устойчивую САУ первого порядка. Для нее характеристическое уравнение имеет вид:
D(p) = a0(j – p1).
Годограф такой САУ обязательно начнется на положительной части вещественной оси. При изменении частоты от 0 до фаза будет изменяться от 0 до /2. (рис. 34).
Рис. 34. Вид годографа Михайлова для устойчивой
и неустойчивой САУ первого порядка
Таким образом, годограф будет полностью находиться в первом квадранте комплексной плоскости.
Для устойчивой САУ второго порядка имеет место следующее уравнение (два сомножителя).
D(p) = a0(j – p1) (j – p2).
Как известно, при построении годографа фазы для каждого сомножителя складываются. Поэтому, для корней с отрицательными вещественными частями результирующий угол поворота годографа при изменении частоты от 0 до будет равен и годограф будет находиться в квадрантах 1 и 2.
Аналогично можно рассмотреть САУ любого порядка.
Для неустойчивой системы фаза, определяемая корнем с положительной вещественной частью, изменяется от 0 до –/2 и результирующий угол поворота годографа будет меньше.
2. Критерий устойчивости Найквиста.
Он позволяет судить об устойчивости замкнутой системы по виду годографа передаточной функции разомкнутой системы
Обычно передаточная функция представляется в виде отношения полиномов, причем степень числителя меньше степени знаменателя.
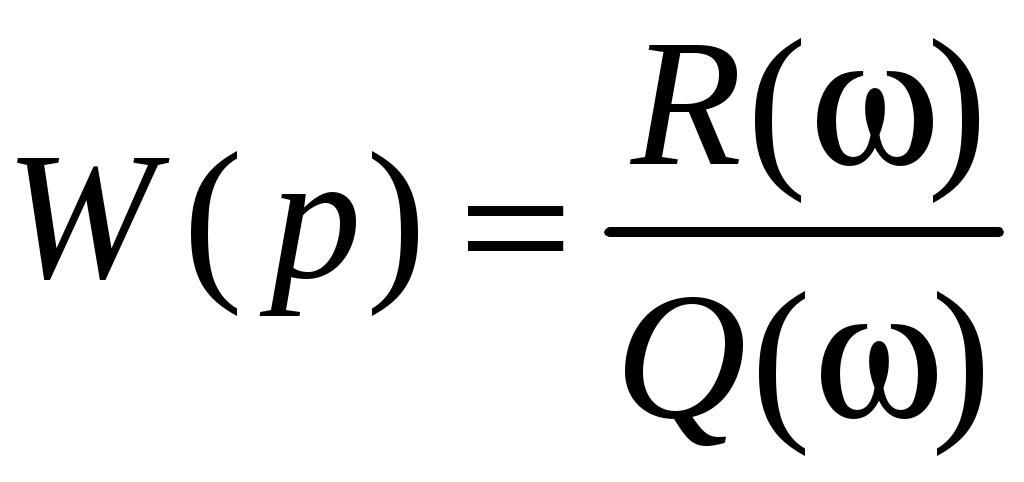 .
.Из последнего замечания следует, что при частоте, стремящейся к бесконечности, годограф всегда стремится к началу координат.
Для определения критерия нужно знать, что полюса передаточной функции – это корни ее знаменателя, а нули – это корни числителя.
Критерий формулируется следующим образом.
Если разомкнутая система устойчива или нейтральна, то для устойчивости в замкнутом состоянии необходимо и достаточно, чтобы годограф не охватывал точку с координатами (–1, j0).
Если разомкнутая система неустойчива, то для того, чтобы она была устойчивой в замкнутом состоянии, необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов годографом отрезка вещественной оси ]–∞, –1[была равнаl/2, где l – число полюсов с положительной вещественной частью передаточной функции разомкнутой системы.
Годограф передаточной функции разомкнутой системы имеет несколько типовых конфигураций в зависимости от параметров системы. Рассмотрим их для случая статической и астатической САУ.
Статическая система.
Для этой системы в знаменателе передаточной функции разомкнутой системы нет множителя
р.
Так как множитель р отсутствует, то значению частоты = 0 (начало годографа) соответствует точка на положительной части вещественной оси.
Введем вспомогательную передаточную функцию W1(p):
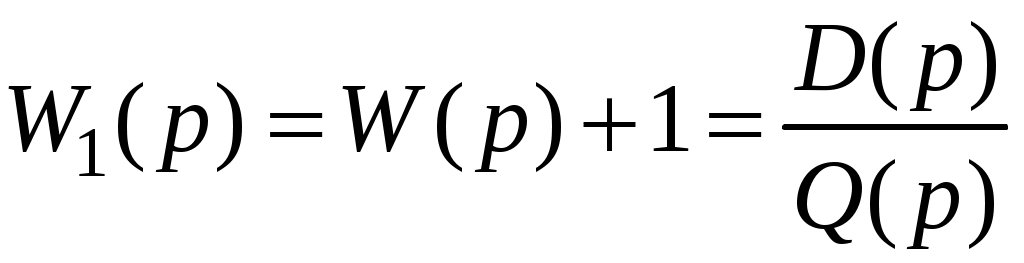 ,
,где D(p) – характеристический полином (используется в критерии устойчивости Михайлова).
Для этой вспомогательной функции в случае устойчивой системы при изменении частоты от 0 до ∞ фаза числителя изменяется на угол (n/2), а фаза знаменателя – на (–n/2), где n – порядок полинома.
Результирующий сдвиг фаз равен нулю, следовательно, годограф передаточной функции W1(p) не должен охватывать начало координат. Годограф же основной функции W(p) не должен охватывать точку с координатами (–1, j0). Таким образом, качественный вид годографа САУ, устойчивой в разомкнутом состоянии, следующий (рис. 35).
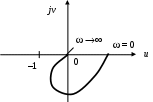
Рис. 35. Годограф передаточной функции устойчивой статической САУ
Для системы, неустойчивой в разомкнутом состоянии, годограф имеет вид (рис. 36):
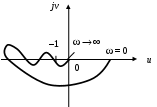
Рис. 36. Годограф статической САУ, неустойчивой в разомкнутом состоянии
Астатическая система.
В знаменателе передаточной функции разомкнутой системы есть сомножители р в разной степени. Например,
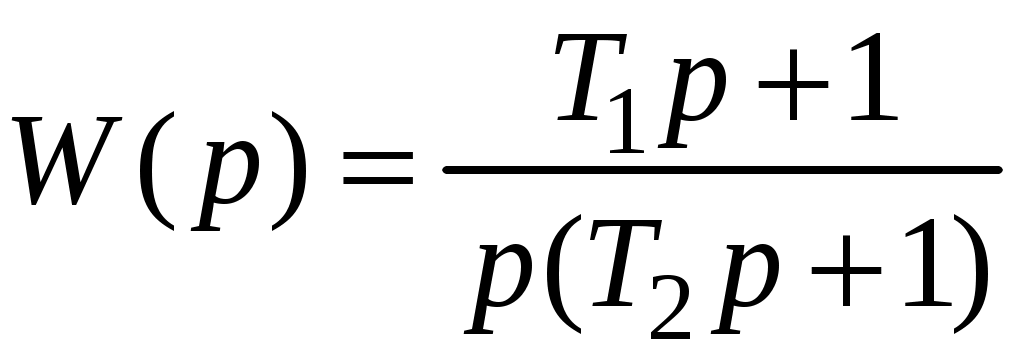 .
.Поэтому, значению частоты = 0 соответствует точка на комплексной плоскости (0, –j ∞)
В этом случае, чтобы оценить устойчивость, нужно дополнить годограф окружностью бесконечного радиуса, двигаясь по часовой стрелке, начиная от положительной части вещественной оси (рис. 37).
Критерий устойчивости Найквиста позволяет определить запас устойчивости по амплитуде и фазе (рис.38).
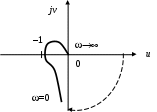
Рис. 37. Годограф передаточной функции устойчивой астатической САУ
Запас по амплитуде позволяет определить, насколько можно изменять общий коэффициент усиления САУ (обычно, увеличить), не нарушая устойчивость.
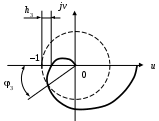
Рис. 38. Определение запаса устойчивости по амплитуде и фазе
Запас устойчивости по фазе позволяет задать допустимый дополнительный сдвиг фазы сигнала при прохождении его через САУ без нарушения условия устойчивости.
3. Логарифмический критерий устойчивости.
Для этого критерия необходимо иметь логарифмические характеристики разомкнутой САУ.
Критерий формулируется следующим образом.
Для того чтобы САУ была устойчива в замкнутом состоянии, необходимо и достаточно, чтобы ЛФЧХ передаточной функции разомкнутой системы не пересекала уровень – или пересекала его четное число раз в пределах положительной части ЛАЧХ (рис. 39).
Данный критерий является развитием критерия устойчивости Найквиста. С его помощью также можно получить значения запаса устойчивости по амплитуде и фазе.
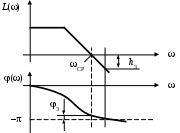
Рис. 39 . Логарифмический критерий устойчивости
9.3. Качество переходного процесса
9.3.1. Показатели качества
Требования к качеству процесса управления в каждом конкретном случае могут быть различными, но как правило, оценивается характер переходного процесса при единичном ступенчатом воздействии (рис. 40).
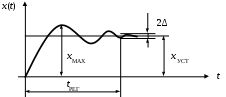
Рис. 40. Показатели качества переходного процесса
Используются следующие показатели качества переходного
процесса.
1. tРЕГ – время регулирования (длительность переходного процесса), время, в течение которого, начиная с момента приложения входного воздействия, отклонение выходной величины от ее установившегося значения, становится меньше наперед заданного значения ∆. Обычно выбирается ∆ = 5% от хУСТ.
2. Перерегулирование:
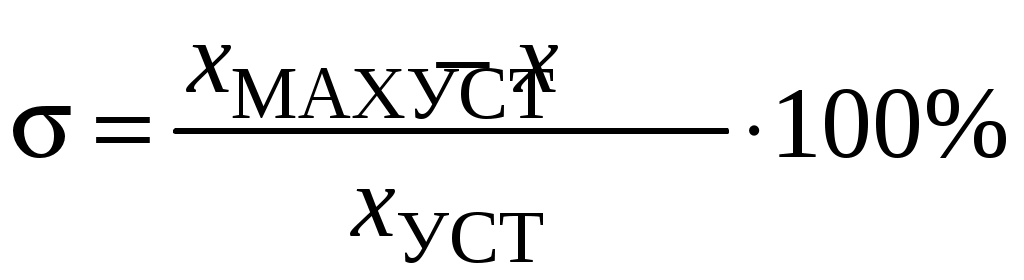 .
.3. Колебательность – число полных колебаний выходной величины за время регулирования.
4. Установившаяся ошибка – это разность между задающим воздействием и установившимся значением выходной величины.
9.3.2. Получение графика переходного процесса
Переходный процесс можно получить несколькими способами:
-
решение дифференциального уравнения; -
использование передаточных функций и прямого и обратного преобразования Лапласа или Фурье; -
использование вещественной части частотной характеристики замкнутой системы.
Первые два способа были представлены выше. Рассмотрим подробнее третий способ.
Как известно, обратное преобразование Фурье имеет вид:
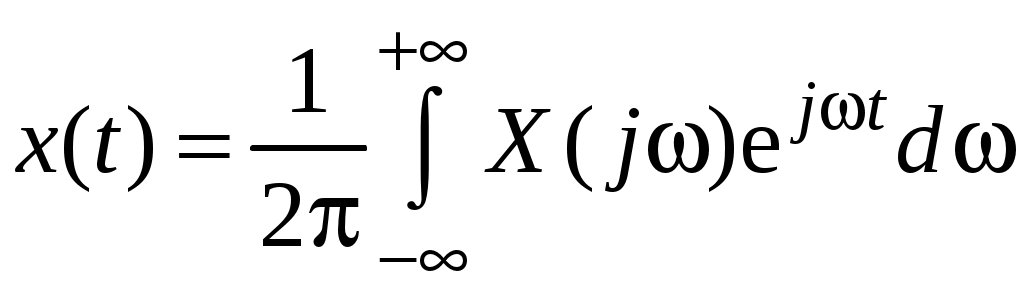 .
.Изображение по Фурье выходной величины:
где
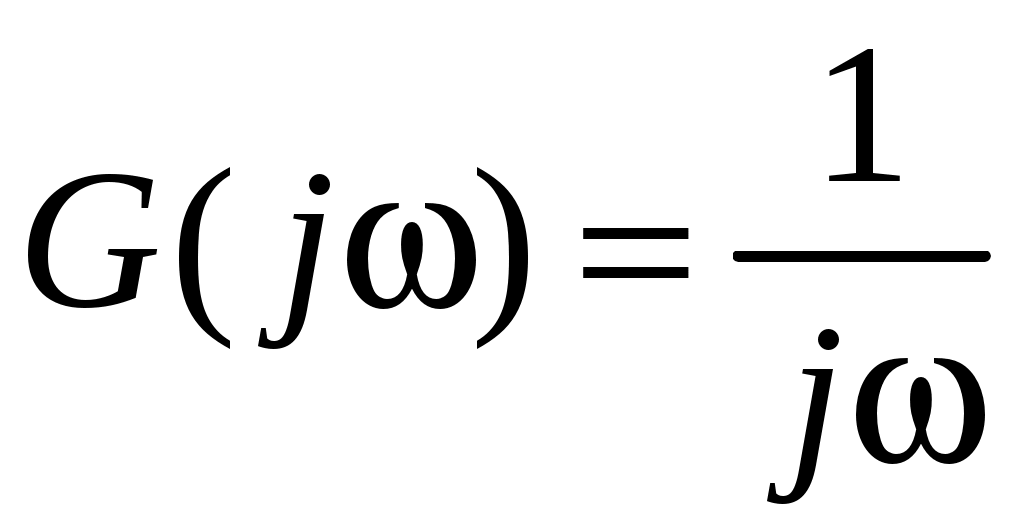 – изображение входного сигнала 1(t);
– изображение входного сигнала 1(t);