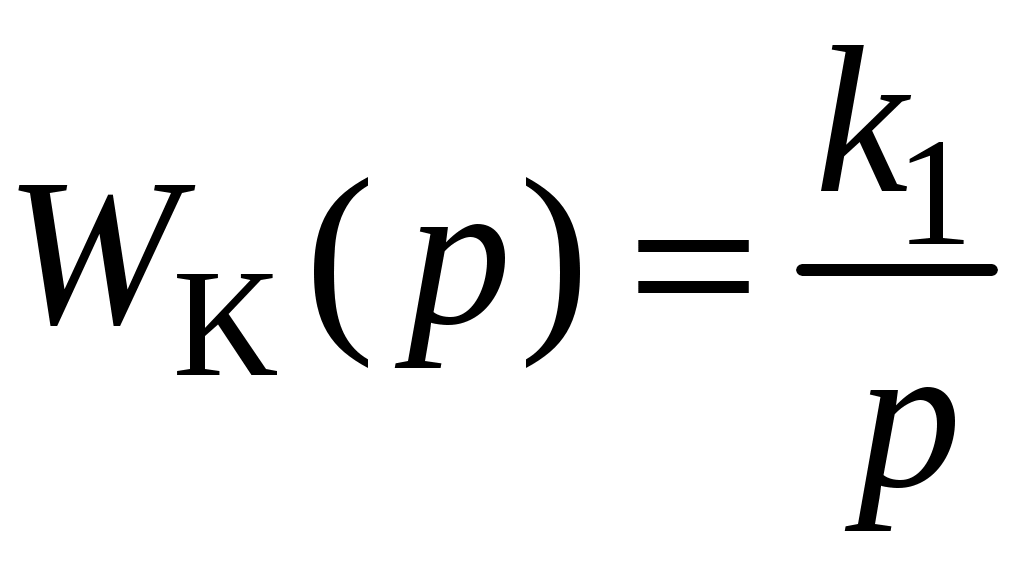Файл: Учебное пособие Рыбинск 2007 удк 681. 5 Павлов Р. В. Основы теории управления. Учебное пособиергата. Рыбинск, 2007. 83 с.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 296
Скачиваний: 2
СОДЕРЖАНИЕ
1. Основные понятия и определения
3. Дифференциальные уравнения ипередаточные функции
5. Типовые звенья САУ и их характеристики
6. Построение передаточных функций САУ
7. Составление исходных дифференциальныхуравнений САУ
9. Процесс управления и требования к нему
9.1. Оценка устойчивости линейной САУ
9.3. Качество переходного процесса
10.2. Типы корректирующих устройств
10.3. Пример синтеза последовательного корректирующего устройства
10.4. Пример синтеза параллельного корректирующего устройства
11.3. Определение передаточных функций элементов системы
11.4. Построение структурной схемы системы
11.5. Построение логарифмических частотных характеристик разомкнутой системы
11.6. Определение устойчивости и запасаустойчивости по амплитуде и фазе
11.7. Определение критического значения добротностис помощью критерия Гурвица
11.8. Введение скоростной обратной связи
11.9. Нахождение минимального коэффициентаскоростной обратной связи
11.10 Определение оптимального коэффициентаскоростной обратной связи
12.2. Характеристики случайных величин и процессов
12.3. Прохождение случайного сигнала через линейную непрерывную систему
12.4. Расчет установившейся ошибки САУ
12.5. Расчеты по минимуму ошибки
13.1. Общий метод составления уравнений нелинейных САУ
13.3. Устойчивость по Ляпунову
где P() – действительная часть (вещественная); это полином, содержащий слагаемые с четными степенями частоты ;
Q() – мнимая часть выражения, содержит слагаемые с нечетными степенями частоты .
Заменив пределы интегрирования, применив формулу Эйлера и оставив только P(), получим
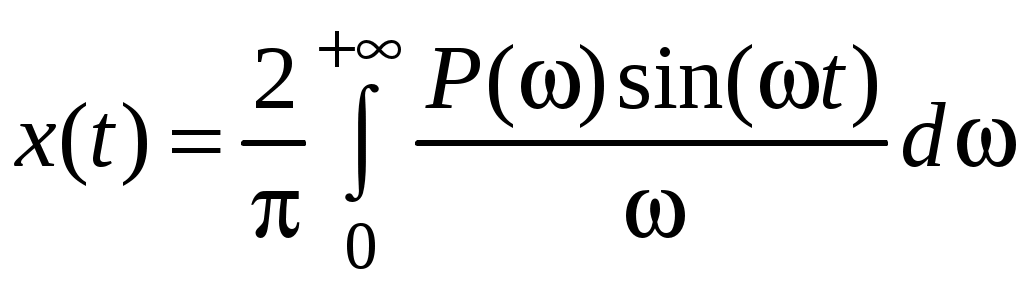 .
.Аналитическое решение данного уравнения представляет собой достаточно сложную задачу. Поэтому существуют приближенные методы решения. Один из них называется методом Солодовникова.
9.3.3. Метод Солодовникова
Здесь вводится понятие типовой единичной трапецеидальной вещественной характеристики. Ее высота равна 1, частота среза (частота положительности) п =1 (рис. 41).
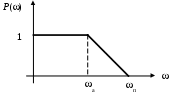
Рис. 41. Типовая единичная трапецеидальная вещественная характеристика
Для данной трапеции существуют таблицы связи выходной величины х(t) от коэффициента наклона = а / п.
Метод заключается в выполнении следующей последовательности действий.
1. Строится график вещественной части частотной передаточной функции замкнутой системы.
2. График разбивается на трапеции. Эта процедура представлена на рис. 42. В данном примере получилось три типовые трапеции.
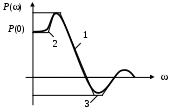
Рис. 42. Разбиение графика вещественной характеристики на трапеции
3. Для каждой трапеции по таблицам находятся значения выходного процесса x1(t), x2(t), x3(t).
4. Находится результирующий график выходного сигнала путем сложения графиков x1(t), x2(t), x3(t).
Так как таблицы разработаны для единичной трапеции, то при построении переходного процесса для каждой трапеции, необходимо использовать правила (формулы) перехода к реальному значению отсчетов выходного сигнала.
1. Получение установившегося значения P(0) = x(∞) = xУСТ.
2. Получение действительной амплитуды сигнала
3. Изменение масштаба времени
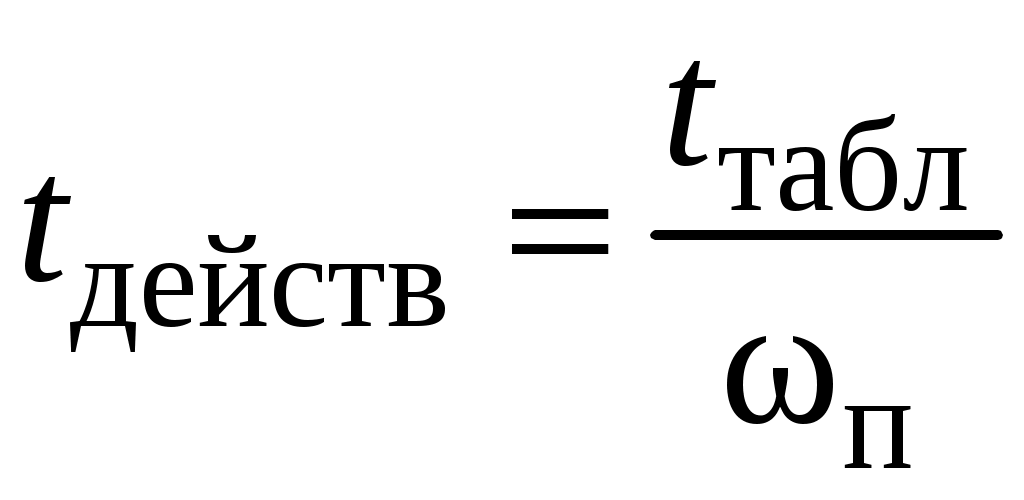 .
.Показатели качества переходного процесса можно приближенно оценить по вещественной частотной характеристике замкнутой системы, не выполняя вышерассмотренных вычислений. Все разновидности графика этой характеристики представлены на рис. 43.
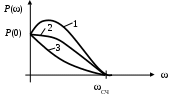
Рис. 43. Типовой вид графиков вещественной характеристики
1 – график характеристики имеет «горб»;
2 – «горба» нет, производная
3 – «горба» нет,
В случае 1 переходный процесс х(t) имеет перерегулирование, причем его величина более 18%.
В случае 2 переходный процесс х(t) имеет перерегулирование, причем его величина менее 18%.
В случае 3 процесс управления монотонный.
По графику можно приближенно определить и время переходного процесса
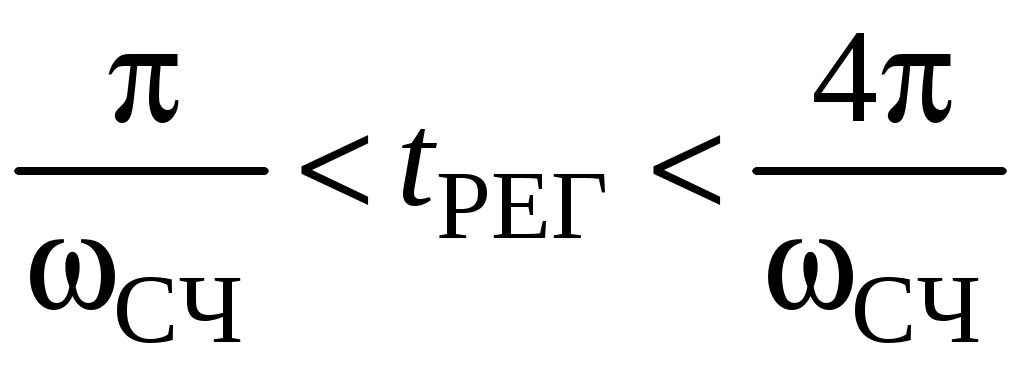 ,
,где СЧ – диапазон существенных частот. Характеристика Р() в этом диапазоне превышает некоторый уровень . Обычно = 5%.
9.3.4. Показатель колебательности
Этот параметр используется для определения запаса устойчивости. Его можно вычислить по значению модуля частотной передаточной функции замкнутой системы
Показатель колебательности равен отношению
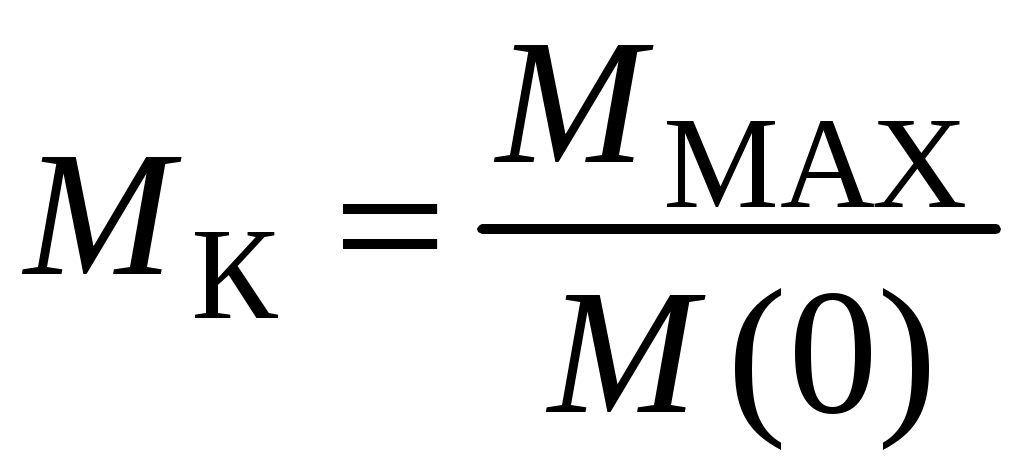 и представлен на рис. 44.
и представлен на рис. 44.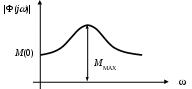
Рис. 44. Модуль частотной передаточной функции замкнутой системы
Это относительная высота резонансного пика. Для упрощения расчетов считается, что М(0) = 1. При этом МК= МMAX.
Физически показатель колебательности – это отношение максимальных значений выходного и входного сигналов САУ.
Чем меньше запас устойчивости САУ, тем больше склонность системы к колебаниям, тем выше резонансный пик. Обычно показатель колебательности лежит в диапазоне 1,1 … 1,5.
Mk можно определить по виду частотной характеристики разомкнутой системы, пользуясь передаточной функцией разомкнутой системы
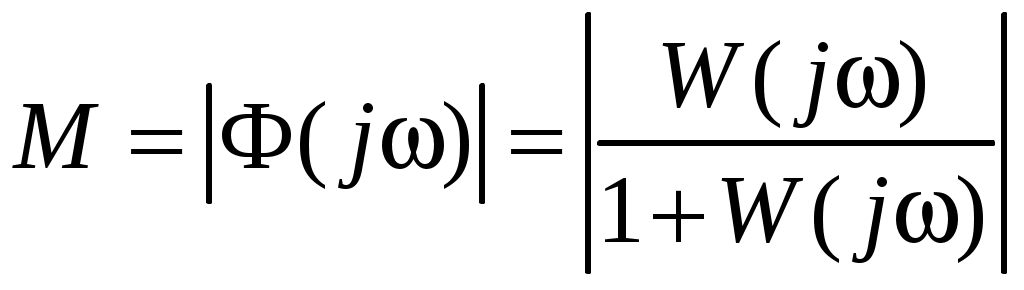 .
.Представив W(j) через действительную U и мнимую V части, получим:
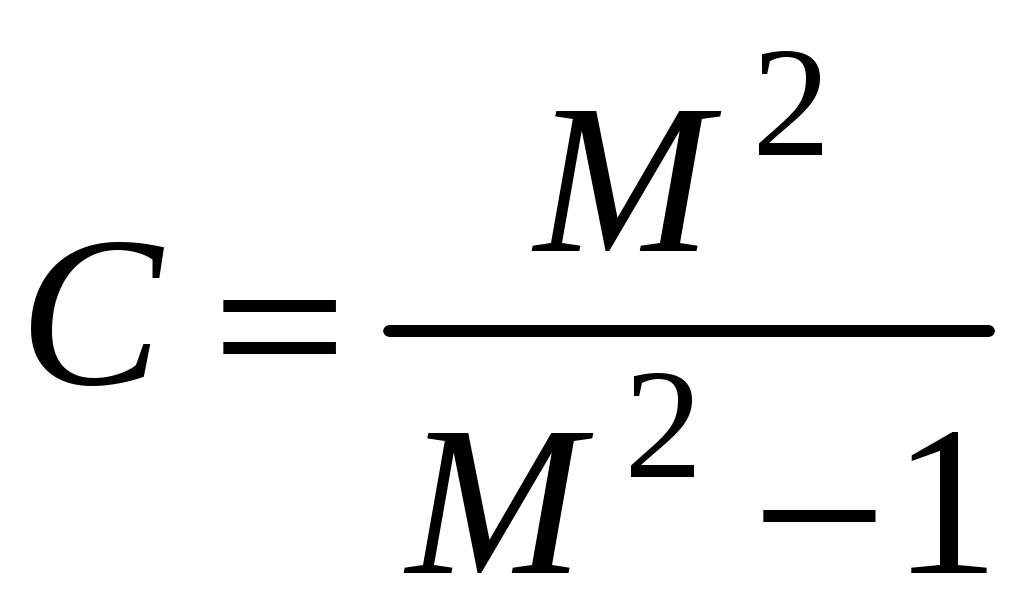 ;
;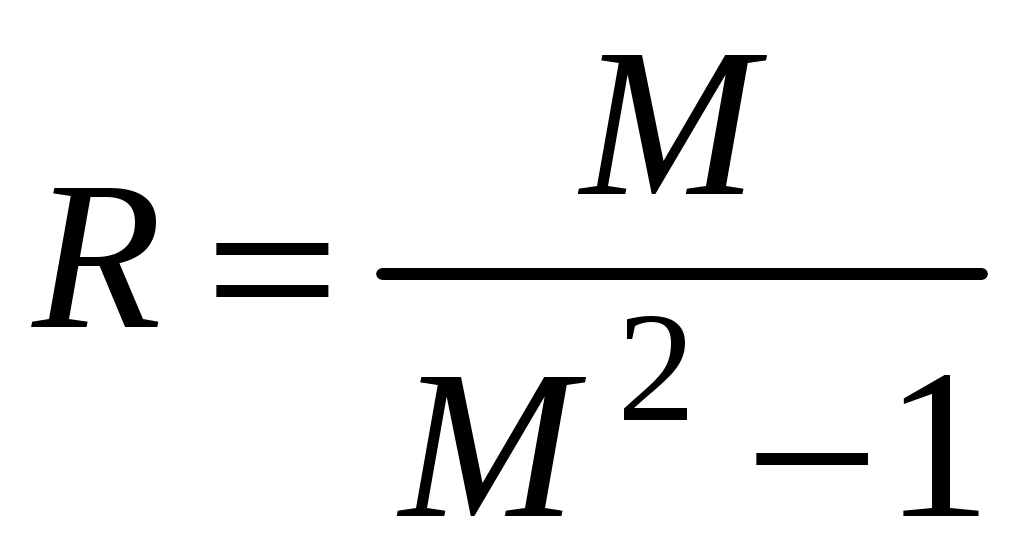 .
.Данные соотношения описывают окружность, причем С – вещественная координата ее центра; R – радиус.
На комплексной плоскости можно построить семейство окружностей с этими параметрами, зависящими от М. На этот график наносится годограф разомкнутой системы (рис. 45).
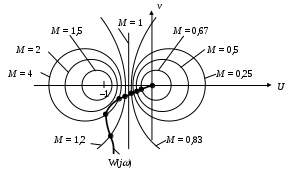
Рис. 45. Семейство окружностей для различных показателей колебательности
На основе этого графика строится график модуля частотной характеристики. Находятся точки пересечения окружностей и годографа. Каждой такой точке соответствует значение модуля М (по окружностям) и значение частоты (по годографу). Пара этих величин представляет координаты точки искомой характеристики (рис. 46).
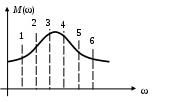
Рис. 46 Построение графика модуля частотной передаточной функции
замкнутой системы
Иногда достаточно определить максимальное значение МMAX (по касанию АФХ соответствующей окружности).
Возможно решение обратной задачи: задается допустимое значение показателя МДОП. Необходимо соответствующим образом спроектировать систему.
Для выполнения этого условия нужно обеспечить, чтобы годограф САУ не заходил в область, ограниченную окружностью с заданным значением М (рис. 47).
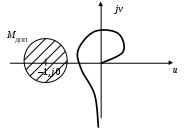
Рис. 47. Допустимая зона параметров САУ по показателю колебательности
9.3.5. Интегральные оценки качества
Это такие оценки, которые одним числом (величиной, параметром) позволяют оценить несколько показателей качества (см. рис. 40).
Например, при помощи соответствующей интегральной оценки можно оценить время переходного процесса и перерегулирование. Эта величина позволяет узнать динамическую ошибку САУ.
В простейшем случае оценку можно получить по формуле:
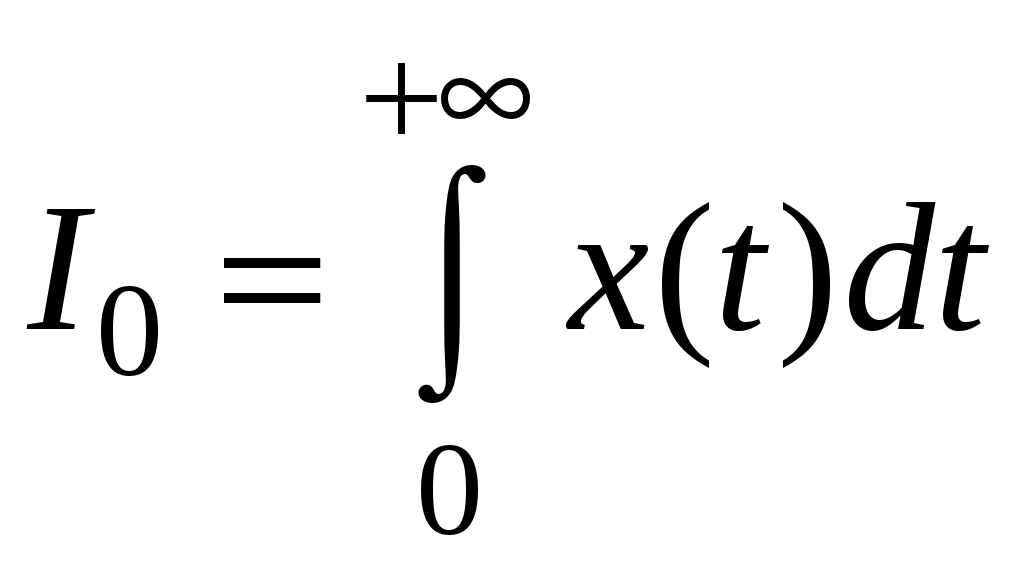 .
.Известна формула преобразования Лапласа:
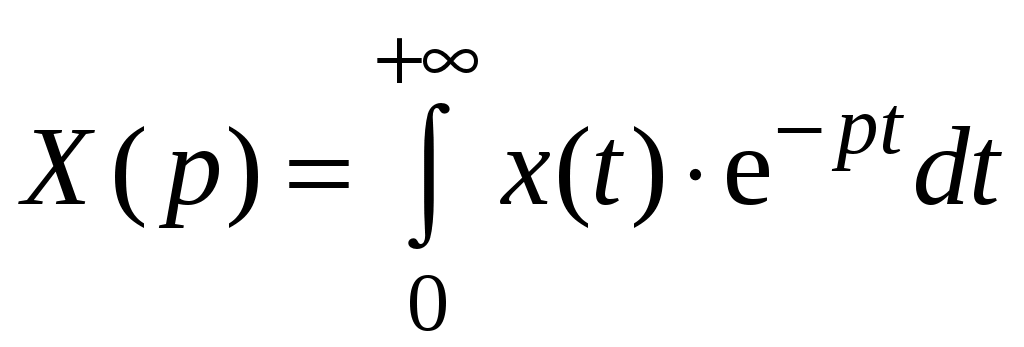 .
.В результате сравнения этих двух уравнений можно получить удобную формулу, позволяющую не вычислять выходной сигнал:
Однако данное соотношение имеет ограниченное применение: оно подходит только для монотонных процессов. Для колебательных процессов используется квадратичная оценка:
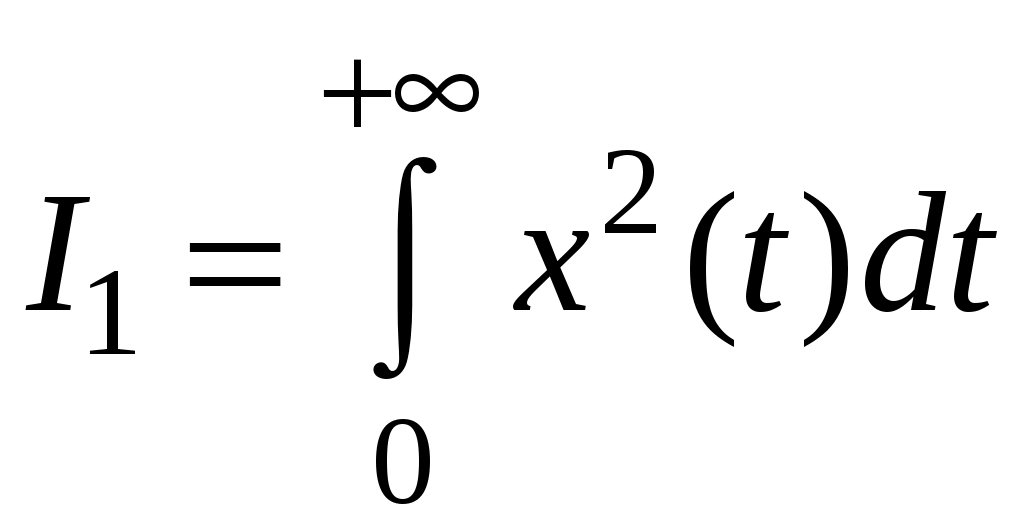 .
.Применяют и другие виды оценок качества, учитывающие изменение скорости, ускорения выходного сигнала. При этом в соответствующих выражениях используются зависимости от производных сигнала.
10. Синтез линейных САУ
10.1. Способы синтеза САУ
Главные цели проектирования САУ – обеспечение устойчивости системы и обеспечение требуемого качества переходного процесса.
Достичь этих целей можно двумя способами.
1. Изменение параметров системы, т. е. изменение параметров звеньев (коэффициент усиления, постоянная времени). В ряде случаев такой подход не приводит к желаемому результату.
2. Изменение структуры системы. Обычно это введение дополнительных устройств или блоков (корректирующих устройств).
Рассмотрим подробнее второй подход.
В теории САУ различают 4 вида корректирующих устройств.
-
Последовательные корректирующие устройства (корректирующие фильтры). -
Параллельные корректирующие устройства, обычно в виде местной обратной связи. -
Корректирующие устройства по внешнему воздействию. -
Неединичная главная обратная связь.
10.2. Типы корректирующих устройств
10.2.1. Последовательные корректирующие устройства
Способ их включения в структуру САУ представлен на рис. 48.

Рис. 48. Последовательное корректирующее устройство
W0(p) – передаточная функция разомкнутой САУ в исходном
состоянии;
WК(p) –передаточная функция корректирующего звена.
Рассмотрим несколько частных случаев.
1. Пропорциональное звено.
Использование такого звена является простейшим случаем
коррекции.
Как было рассмотрено выше, звено описывается соотношениями:
При этом повышается статическая точность системы, но снижается устойчивость и качество переходного процесса. Такое звено используется редко.
2. Интегрирующее корректирующее звено.
Его характеристики имеют вид: