Файл: Курс лекций по дисциплине Эконометрика.doc

1. Если среди парных коэффициентов корреляции между объясняющими переменными имеются значения 0,75-0,80 и выше, это свидетельствует о присутствии мультиколлинеарности.

Пример. В примере 2 между переменными K и L коэффициент корреляции равен 0,96, а между lnK и lnL чуть меньше 0,89. 

2. О присутствии явления мультиколлинеарности сигнализируют некоторые внешние признаки построенной модели, являющиеся его следствиями:

- некоторые из оценок , j=1,2,…,k имеют неправильные с точки зрения экономической теории знаки или неоправданно большие по абсолютной величине значения,

- небольшое изменение исходной выборки (добавление или изъятие малой порции данных) приводит к существенному изменению оценок коэффициентов модели вплоть до изменения их знаков,

- большинство оценок коэффициентов регрессии оказываются статистически незначимо отличающимися от нуля, в то время как в действительности многие из них имеют отличные от нуля значения, а модель в целом является значимой при проверке с помощью F-критерия.

Методы устранения мультиколлинеарности.

1. Проще всего удалить из модели один или несколько факторов.

2. Другой путь состоит в преобразовании факторов, при котором уменьшается корреляция между ними. Например, при построении регрессий на основе временных рядов помогает переход от первоначальных данных к первым разностям =Y_t-Y_t-1. В примере 2 переход от переменных K и L к их логарифмам уменьшил коэффициент корреляции с 0,96 до 0,89.

3. Использование в уравнении регрессии взаимодействия факторов, например, в виде их произведения.

4. Использование так называемой ридж-регрессии (гребневой регрессии). В этом случае к диагональным элементам системы (3.6) добавляется "гребень"  (небольшое число, как правило, от 0,1 до 0,4):

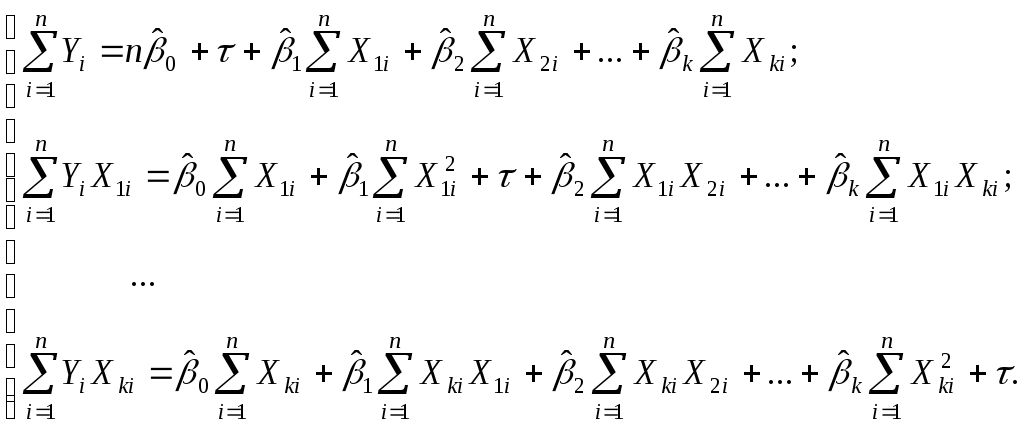
Это делает получаемые оценки смещенными, но уменьшает средние квадраты ошибок коэффициентов.

5. Использование метода главных компонент⁶.

6. Отбор наиболее существенных объясняющих переменных на основе методов исключения, включения, шаговой регрессии, которые используют для принятия решения

---

F-критерий.

4. Спецификация переменных в уравнениях регрессии
4.1. Спецификация уравнения регрессии и ошибки спецификации
При построении эконометрической модели исследователь специфицирует составляющие ее соотношения, выбирает переменные, входящие в эти соотношения, а также определяет вид математической функции, представляющей каждое соотношение. Остановимся на вопросе выбора переменных, которые должны быть включены в модель. До сих пор мы неявно считали, что имеем правильную спецификацию модели.

На практике никогда не получается правильная спецификация модели, возникают так называемые ошибки спецификации. Экономическая теория, положения которой используются при выборе регрессоров, не может быть совершенной. Поэтому исследователь может включить в эконометрическую модель переменные, которых там не должно быть, и может не включить другие переменные, которые должны там присутствовать.

Т.е. изучим две ситуации.

Случай 1. Исключены существенные переменные.

Процесс, порождающий данные:

, i=1,…,n. (4.1а)

Модель:

(4.1б)

Случай 2. Включены несущественные переменные.

Процесс, порождающий данные:

(4.2а)

Модель:

, i=1,…,n (4.2б)

Часто регрессию (4.1а) называют длинной, а регрессию (4.1б) – короткой.
В первом случае, если опущены переменные, которые должны быть включены в регрессию, оценки коэффициентов , j=1,…,k являются, вообще говоря, смещенными (но обладают меньшей дисперсией) за исключением двух случаев, когда =0, j=1,…,l или регрессоры X₁,…, X_k и Z₁,…, Z_l ортогональны.

Смещенной является и оценка дисперсии случайной ошибки

---

, а, следовательно, стандартные ошибки и многие статистические тесты, в которых используется значение , становятся некорректными.

Во втором случае, если включены переменные, которые не должны присутствовать в модели, оценки коэффициентов , j=1,…,k будут несмещенными, но неэффективными. Поскольку несмещенность оценок и величины дисперсии сохраняется, возникает иллюзия, что надо включать в модель как можно больше регрессоров. Но в этом случае падает точность оценок, и может возникнуть проблема мультиколлинеарности объясняющих переменных.

На практике, однако, нам неизвестен процесс, порождающий данные, т.е. мы не знаем истинную модель. Поэтому, как правило, возникает проблема – какую модель выбрать: короткую или длинную, т.е. включать дополнительные регрессоры в модель или не включать: в первом случае мы получим смещенные оценки коэффициентов регрессии, а во втором случае – неэффективные оценки. Решение этой проблемы может быть найдено на основе критерия минимума среднеквадратичного отклонения значений коэффициентов, см. [5, с. 112-114].

Часто случается также, что исследователь не может использовать данные по переменным, которые включены в модель. Некоторые переменные, например, невозможно измерить, другие поддаются измерению, но это достигается большими затратами времени и ресурсов. В таких случаях вместо отсутствующих переменных полезно использовать некоторые их заменители (proxy).

Например, если вы не имеете данных о качестве образования, вы можете использовать показатель качества образования как отношение числа преподавателей к числу студентов или денежные расходы на одного студента.

Причин использования "прокси"-переменных две: во-первых, если пропущена важная для модели переменная, то оценки будут смещены (случай 1 выше), а, во-вторых, результаты оценки регрессии с включением замещающих переменных могут дать косвенную информацию о тех переменных, которые замещены данными переменными.

4.2. Обобщенный метод наименьших квадратов
Обобщим КЛММР вида (3.1). Пусть по-прежнему мы располагаем выборочными наблюдениями над

---

k переменными Y_i и , j=1,..., k, i=1,2,…,n и строим регрессию:

(4.3)

Откажемся от предположения КЛММР о некоррелированности и гомоскедастичности случайной ошибки (3.3). То есть относительно переменных модели в уравнении (4.3) примем следующие основные гипотезы:

E(u_i)=0; (4.4)

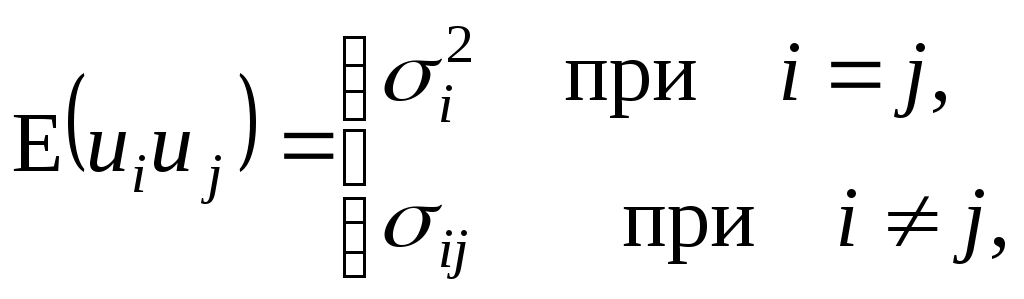(4.5)

X₁, X₃, ..., X_k – неслучайные переменные; (4.6)

Не должно существовать строгой линейной

зависимости между переменными X₁, X₃, ..., X_k. (4.7)

Суть гипотезы (4.5) в том, что все случайные ошибки u_i имеют непостоянную дисперсию, то есть не выполняется условие гомоскедастичности дисперсии – имеет место гетероскедастичность дисперсии ошибок. Кроме того, ковариации остатков могут быть произвольными и отличными от нуля (вторая строчка соотношения (4.5)).

Модель вида (4.3)-(4-7) называется обобщенной линейной моделью множественной регрессии (ОЛММР). Отличие ОЛММР от КЛММР состоит в изменении предположений о поведении случайной ошибки (4.5).

К ОЛММР может быть применен метод наименьших квадратов, однако (3.6) оказывается неприменимой к модели (4.3)-(4-7) в силу потери свойства оптимальности оценок. Но МНК к ОЛММР может быть применен.

Критерий минимизации суммы квадратов ошибок МНК в силу условия (4.5) заменяется на другой – минимизация обобщенной суммы квадратов отклонений (с учетом ненулевых ковариаций случайной ошибки для разных наблюдений и непостоянной дисперсии ошибки) и соответственно усложняется вид системы уравнений для определения оценок коэффициентов по сравнению с системой (3.6) для МНК. После решения полученной системы линейных алгебраических уравнений получим линейные несмещенные оценки коэффициентов ОЛММР, которые будут эффективными. Указанный метод получения оценок называется обобщенным методом наименьших квадратов (ОМНК) или методом Айткена.

Обозначим⁶:

; .

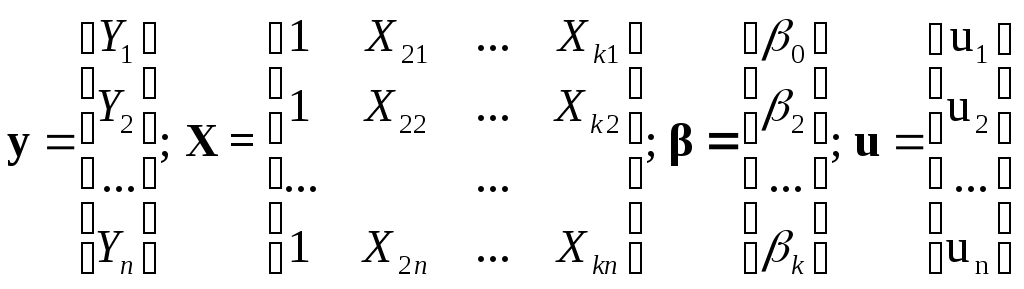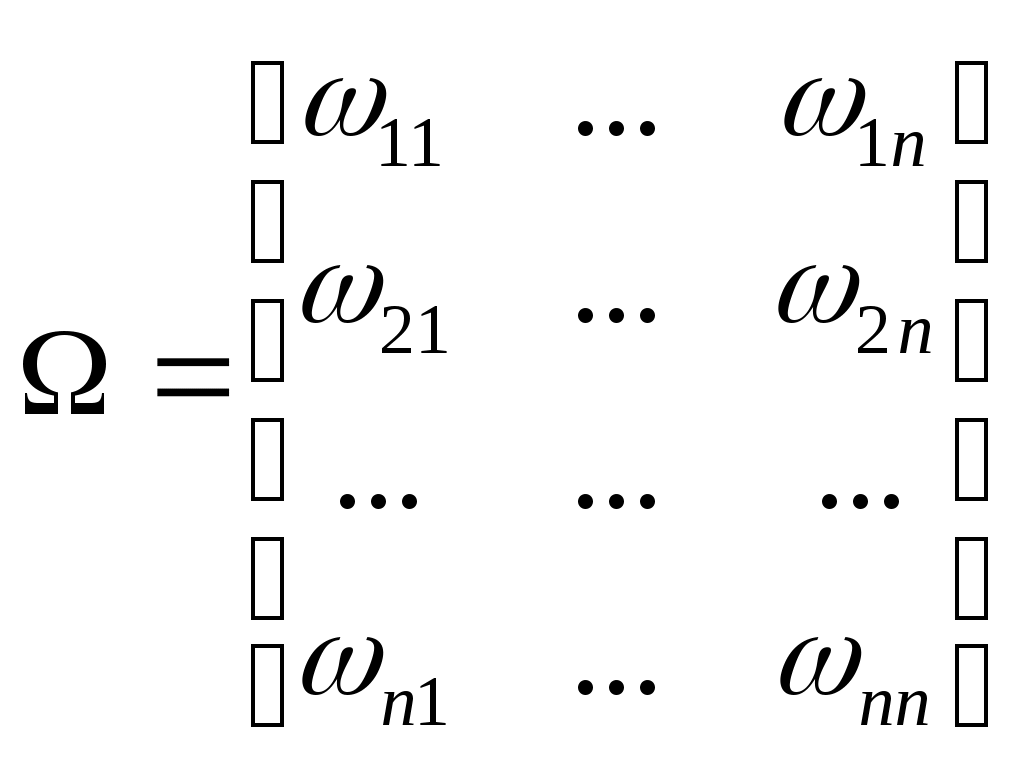Тогда модель (4.3)-(4.7) запишется в матричном виде:

y=X+u,

при условиях

E(u)=0;

E(uu^T

---

)=²;

X – не из случайных чисел;

rank(X)=k+1
Оценки МНК получаются по формуле . Оценки ОМНК получаются по формуле .

Подчеркнем, что для применения ОМНК в (4.5) необходимо знать значения в правой части равенства (в частности элементы матрицы ), что на практике случается крайне редко. Поэтому каким-либо способом оценивают величины i, j=1,…,n. А затем используют эти оценки в расчетах коэффициентов модели. Этот подход составляет суть так называемого доступного обобщенного метода наименьших квадратов. Конкретные способы оценки неизвестных ковариаций будут рассмотрены ниже.
4.3 Линейная модель множественной регрессии

с гетероскедастичными остатками

Довольно часто при построении регрессии анализируемые объекты неоднородны, например, при исследовании структуры потребления домохозяйств естественно ожидать, что колебания в структуре будут выше для богатых, чем для бедных домохозяйств. В этой ситуации предположение (3.3) о постоянстве дисперсии случайной ошибки (имеется в виду возможное поведение случайного члена до того, как сделана выборка) оказывается не соответствующим действительности. В случаях, когда дисперсия u одинакова в каждый момент времени или для каждого значения X, существуют определенные ограничения (в некоторой полосе) для расположения точек на графике X и Y, согласно которым отчетливой тенденции к увеличению или уменьшению дисперсии по мере роста X не наблюдается.

На рис. 4.1 приводятся примеры изменения разброса (гетероскедастичности) случайной ошибки регрессии.

На рис. 4.1а изображена ситуация, когда значения дисперсии растут по мере увеличения значений регрессора X. На рис. 4.1б дисперсия ошибки достигает максимальной величины при средних значениях X, уменьшаясь по мере приближения к крайним значениям. Наконец, на рис. 4.1в дисперсия ошибки оказывается наибольшей при малых значениях X, быстро уменьшается и становится однородной по мере увеличения независимой переменной

---