ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 380
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
2.2. Постановка задачи регрессии
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
3. Классическая линейная модель множественной регрессии
3.2. Оценивание коэффициентов КЛММР
Для того чтобы получить адекватную оценку того, насколько хорошо вариация результирующего признака объясняется вариацией нескольких факторных признаков, применяют скорректированный коэффициент детерминации
Скорректированный коэффициент детерминации всегда меньше R2. Кроме того, в отличие от R2, который всегда положителен,
Пример (продолжение примера 1). Рассчитаем множественный коэффициент корреляции, согласно формуле (3.20):
Величина множественного коэффициента корреляции, равного 0,8601, свидетельствует о сильной взаимосвязи стоимости перевозки с весом груза и расстоянием, на которое он перевозится.
Коэффициент детерминации равен: R2=0,7399.
Скорректированный коэффициент детерминации рассчитываем по формуле (3.22):
Заметим, что величина скорректированного коэффициента детерминации отличается от величины коэффициента детерминации.
Таким образом, 70,9% вариации зависимой переменной (стоимости перевозки) объясняется вариацией независимых переменных (весом груза и расстоянием перевозки). Остальные 29,1% вариации зависимой переменной объясняются факторами, неучтенными в модели.
Величина скорректированного коэффициента детерминации достаточно велика, следовательно, мы смогли учесть в модели наиболее существенные факторы, определяющие стоимость перевозки.
3.5. Оценка качества модели множественной регрессии
Проверка качества модели множественной регрессии может быть осуществлена с помощью дисперсионного анализа.
Как уже было отмечено (см. 2.5), сумма квадратов отклонений от среднего в выборке равна сумме квадратов отклонений значений
плюс сумма квадратов отклонений Y от линии регрессии
С учетом (3.21) получим таблицу дисперсионного анализа (табл. 3.4), аналог таблицы 2.3.
Проверка качества модели множественной регрессии в целом может быть осуществлена с помощью F-критерия Фишера. Для проверки гипотезы о том, что линейная связь между
воспользуемся соотношением
которое удовлетворяет F - распределению Фишера с (k, n-(k+1)) степенями свободы. Критические значения этой статистики F для уровня значимости затабулированы.
Таблица 3.4
Таблица дисперсионного анализа
| Источник вариации | Сумма квадратов отклонений | Число степеней свободы | Дисперсия на одну степень свободы |
| | | k | |
| Остаток | | n-k-1 | |
| Общая вариация | | n-1 | |
Если F>F, то гипотеза об отсутствии связи между переменными
Пример (продолжение примера 1). Заполним таблицу дисперсионного анализа:
Таблица дисперсионного анализа
| Источник вариации | Сумма квадратов отклонений | Число степеней свободы | Дисперсия |
| | 5828,84 | 2 | 2914,42 |
| Остаток | 2049,54 | 17 | 120,56 |
| Общая вариация | 7878,38 | 19 | |
Получаем
В нашем примере F>F, следовательно, нулевая гипотеза отклоняется, и уравнение множественной регрессии значимо.
Помимо проверки значимости уравнения в целом, можно проверить статистическую значимость каждого из коэффициентов регрессии в отдельности.
Фактически это означает проверку одной из гипотез:
1)
Статистическая значимость каждого из коэффициентов регрессии определяется при помощи t-критерия Стьюдента. Решение о том, что верна нулевая гипотеза, принимается в случае, когда t<t, иначе принимается альтернативная гипотеза.
Значение t-статистики Стьюдента в случае множественной регрессии определяется по формуле:
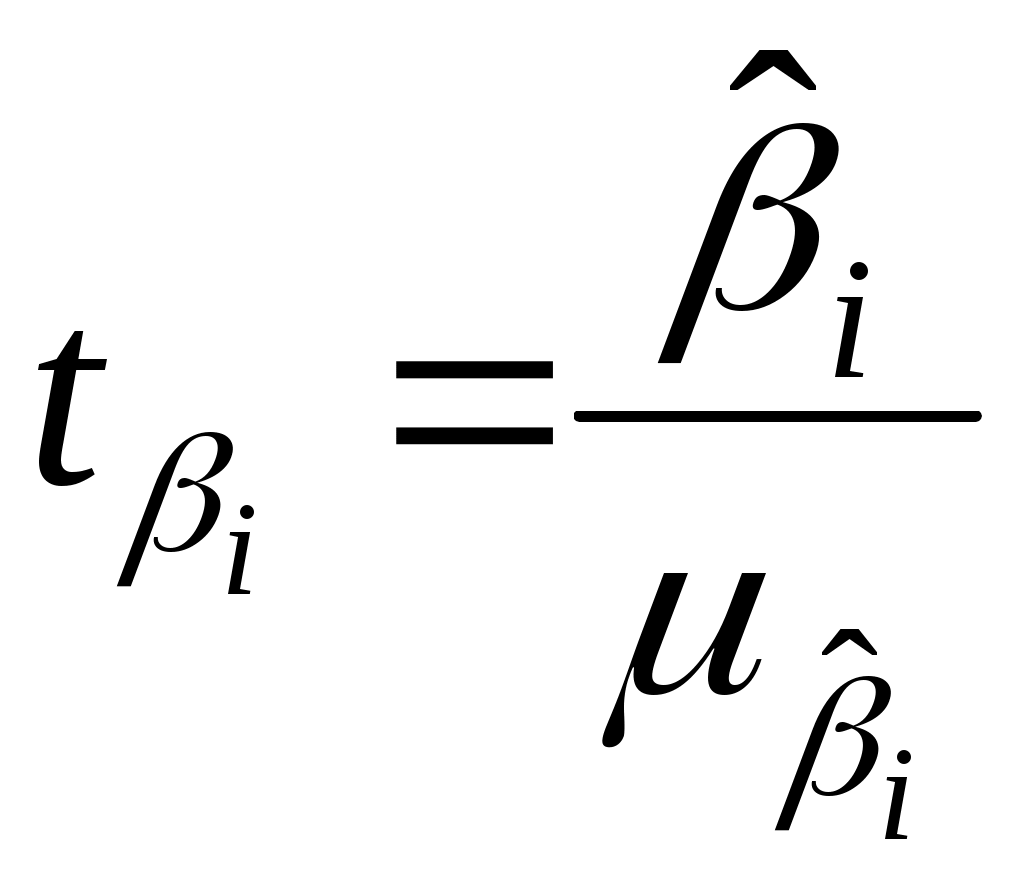 , (3.24)
, (3.24)где
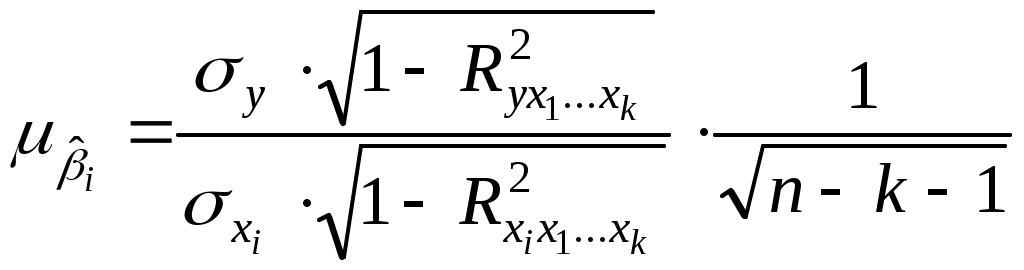 , (3.25)
, (3.25)здесь
Пример (продолжение примера 1). Проверим значимость коэффициентов регрессии. В случае, когда в уравнение регрессии включены две независимые переменные, формула (3.24) упрощается
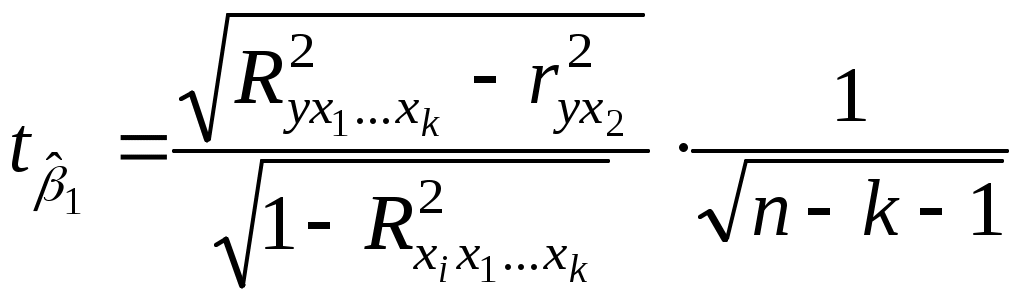 ,
, 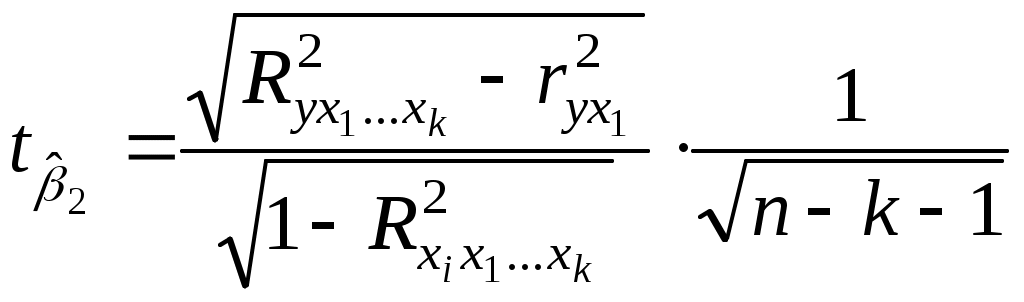 .
.Таким образом:
Так как в обоих случаях
3.6 Мультиколлинеарность и методы ее устранения
Одним из важнейших этапов построения регрессии является отбор факторов
Наиболее широко используются для решения вопроса об отборе факторов частные коэффициенты корреляции, оценивающие в чистом виде тесноту связи между фактором и результатом.
При включении факторов следует придерживаться правила, согласно которому число включаемых в модель объясняющих переменных должно быть в 5-6 раз меньше объема совокупности, по которой строится регрессия. Иначе число степеней свободы остаточной вариации будет мало, и параметры уравнения регрессии окажутся статистически незначимы.
Иногда при отборе переменных-факторов нарушается предположение (3.5). В этом случае говорят, что объясняющие переменные
Реальная (частичная) мультиколлинеарность возникает в случаях достаточно сильных линейных статистических связей между переменными