ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 376
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
2.1. Основные цели и задачи прикладного корреляционно-регрессионного анализа
2.2. Постановка задачи регрессии
2.4. Коэффициент корреляции, коэффициент детерминации, корреляционное отношение
3. Классическая линейная модель множественной регрессии
3.2. Оценивание коэффициентов КЛММР
Поскольку обе переменные измерены в $, то интерпретация облегчается.
Смысл коэффициента
Константа в данном случае не имеет никакого смысла применительно к совокупности, поскольку мы не можем сказать, что при нулевых доходах потребление граждан США составит -2,91 млрд. долларов.
Рассчитаем средний коэффициент эластичности:
Т.е. при изменении личных доходов на 1% от своего среднего значения в среднем по совокупности индивидуальное потребление изменится на 0,923% от своей средней величины.
При интерпретации уравнения регрессии важно помнить о следующих фактах:
-
величины и
и  являются только оценками и , а следовательно, и вся интерпретация представляет собой тоже оценку;
являются только оценками и , а следовательно, и вся интерпретация представляет собой тоже оценку; -
уравнение регрессии отражает общую тенденцию для выборки, а каждое отдельное наблюдение при этом подвержено воздействию случайностей; -
верность интерпретации зависит от правильности спецификации уравнения, то есть включения/исключения соответствующих объясняющих переменных и выбора вида функции регрессии.
3. Классическая линейная модель множественной регрессии
Рассмотрим обобщение линейной регрессионной модели для случая более двух переменных.
Всякий раз, когда изучаемый процесс или явление является результатом совместного действия нескольких факторов, у исследователя возникает потребность в оценке влияния каждого фактора в отдельности. Один из стандартных методов3, позволяющий успешно решить эту задачу, сутьмножественная регрессия.
3.1. Предположения модели
Пусть мы располагаем выборочными наблюдениями над k переменными Yi и
-
1
2
…
i
…
n
Y1,
Y2,
…
Yi,
…
Yn
X11,
X12,
…
X1i,
…
X1n
…
…
…
…
…
…
Xk1,
Xk2,
…
Xki,
…
Xkn
Предположим, что существует линейное соотношение между результирующей переменной Yи k объясняющими переменными X1, X3, ..., Xk. Тогда с учетом случайной ошибки ui запишем уравнение:
В (3.1) неизвестны коэффициенты
, j=0,2,…,kи параметры распределения ui. Задача состоит в оценивании этих неизвестных величин. Модель (3.1) называется классической линейной моделью множественной регрессии (КЛММР). Заметим, что часто имеют в виду, что переменная X0 при 0 равна единице для всех наблюдений i=1,2,…,n.
Относительно переменных модели в уравнении (3.1) примем следующие основные гипотезы:
E(ui)=0; (3.2)
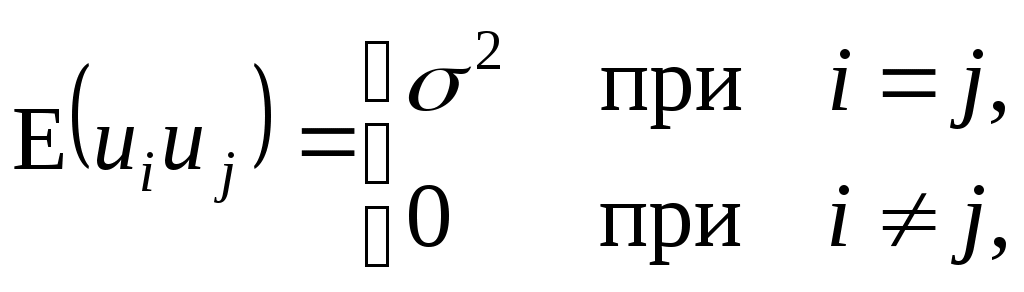 (3.3)
(3.3)X1, X3, ..., Xk – неслучайные переменные; (3.4)
Не должно существовать строгой линейной
зависимости между переменными X1, X3, ..., Xk. (3.5)
Первая гипотеза (3.2) означает, что переменные ui имеют нулевую среднюю.
Суть гипотезы (3.3) в том, что все случайные ошибки ui имеют постоянную дисперсию, то есть выполняется условие гомоскедастичности дисперсии (см. подробнее раздел 4).
Согласно (3.4) в повторяющихся выборочных наблюдениях источником возмущений Y являются случайные колебания ui, а значит, свойства оценок и критериев обусловлены объясняющими переменными X1, X3, ..., Xk.
Последняя гипотеза (3.5) означает, в частности, что не существует линейной зависимости между объясняющими переменными, включая переменную X0, которая всегда равна 1.
Понятно, что условия (3.2)-(3.4) соответствуют своим аналогам для случая двух переменных в п.2.2.
3.2. Оценивание коэффициентов КЛММР
методом наименьших квадратов
Применяя к (3.1) с учетом (3.2)-(3.5) МНК, получаем из необходимых условий минимизации функционала:
т.е. обращения в нуль частных производных по каждому из параметров:
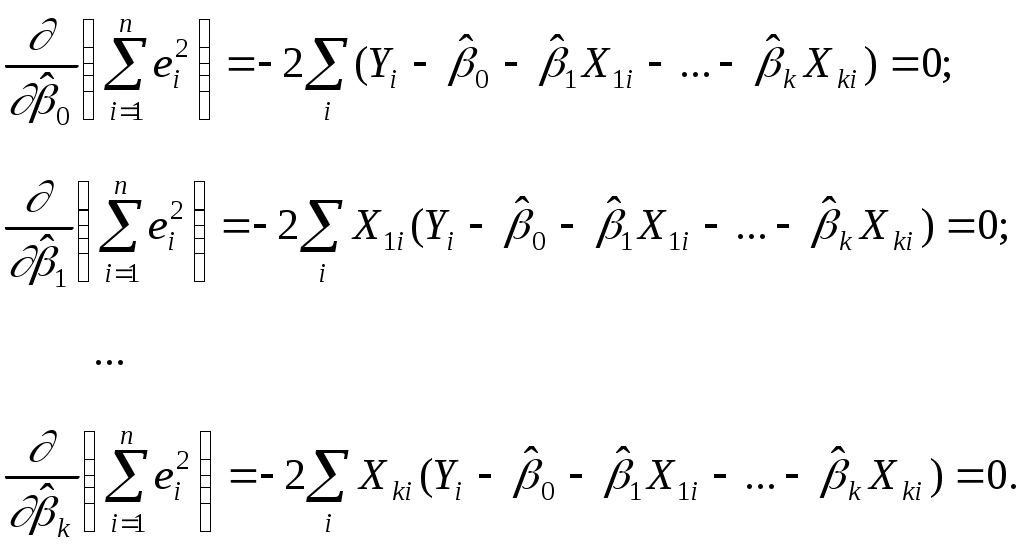
Упростив последние равенства, получим стандартную форму нормальных уравнений, решение которых дает искомые оценки параметров:
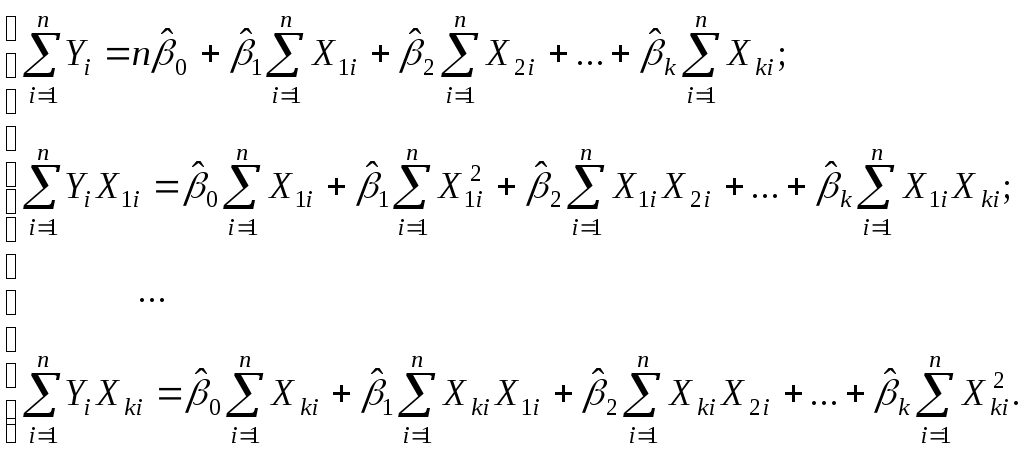 (3.6)
(3.6)Сложность решения системы линейных уравнений (3.6) с (k+1) неизвестными увеличивается быстрее, чем растет k. В зависимости от количества уравнений система может быть решена методом исключения Гаусса или методом Крамера или другим численным методом решения системы линейных алгебраических уравнений.
Поскольку для большинства практических задач изучаются несколько альтернативных спецификаций модели (3.1), то широкое применение ЭВМ, а также специальных статистических пакетов позволяет значительно упростить процедуру оценивания.
В результате решения системы4 (3.6) получим оценки коэффициентов
Возможна и другая запись уравнения (3.1) в так называемом стандартизованном масштабе:
где
для которых среднее значение равно нулю:
а среднее квадратическое отклонение равно единице:
Нетрудно установить зависимость между коэффициентами "чистой" регрессии
причем
Соотношение (3.8) позволяет переходить от уравнения вида (3.7) к уравнению вида (3.1).
Стандартизованные коэффициенты регрессии показывают, на сколько "сигм" изменится в среднем результат (Y), если соответствующий фактор
В силу того, что все переменные центрированы и нормированы, коэффициенты
Нетрудно показать, что оценки МНК
Как было уже указано раньше, достоинством метода множественной регрессии является возможность выделения влияния каждого из факторов Xj в условиях, когда воздействие многих переменных на результат эксперимента не удается контролировать. Степень раздельного влияния каждого из факторов характеризуется оценками
Пример 1. Исследуется зависимость между стоимостью грузовой автомобильной перевозкиY(тыс. руб), весом груза