Файл: Иркутский национальный исследовательский технический университет институт заочновечернего обучения Кафедра Самолётостроения и эксплуатации авиационной техники.docx

3 Построение эпюр внутренних силовых факторов, действующих в сечениях эквивалентного полукрыла

Из трёх внутренних силовых факторов 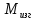, 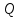и 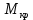, действующих в поперечных сечениях крыла, изгибающий момент можно считать основным, поскольку вес силовых элементов, воспринимающих изгибающий момент, составляет около 50% общего веса крыла [3, стр. 83]. Поэтому проектировочный (приближённый) расчёт крыла выполняется в условии изгиба. Следовательно, принимается, что ось нагрузки и ось жёсткости совпадают.

Для качественной и количественной оценки поведения конструкции полукрыла для расчётного случая криволинейного полета в вертикальной плоскости на небольших углах атаки, выполняется построение эпюр соответствующих внутренних силовых факторов для выбранной расчётной схемы. В качестве расчётной принимается, жёстко зафиксированную в сечении крыла, совпадающим с плоскостью симметрии самолёта. То есть в сечении с центральной хордой 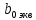. Длина балки равна величине полуразмаха эквивалентного крыла, (см. рис. 2.2). Для анализа работы такой балки на изгиб линии нагружения и жёсткости совмещены с линией 50% хорд.

Балка нагружается неравномерно распределённой нагрузкой с переменной интенсивностью 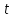, полученной выше и представленной аналитически в таблице 2.2, графически на рисунке 2.4.

Помимо этой нагрузки на крыло действуют массы агрегатов, которые расположены на нём. В выбранном самолете-прототипе такими агрегатами являются две симметрично расположенных мотогондолы двигателей с размещёнными в них основными опорами шасси. Нагрузка, создаваемая каждым двигателем, схематизируется в виде сосредоточенной силы в соответствии с его массой и расчётным случаем.

---

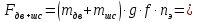
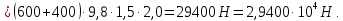
Согласно эскизу самолета-прототипа можно в первом приближении расположить эту сосредоточенную силу в третьем сечении полукрыла с хордой 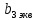(см. рис. 2.2).

Тогда расчётную схему рассматриваемой конструкции полукрыла можно представить так, как это показано на рисунке 3.1, а.

Построение эпюры поперечной силы 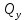, действующей в поперечных сечениях эквивалентного крыла, выполняется, используя процедуру интегрирования по :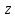

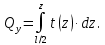
Интегрирование выполняется численно, используя метод трапеций (см. рис. 5). Определение значения поперечной силы начинается с концевого сечения, поскольку наверняка известно, что для построенной расчётной схемы в этом сечении поперечная сила равна нулю:

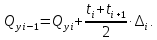
где – номер сечения.

Концевое сечение имеет номер 10, то есть:

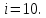
Тогда:





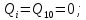
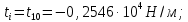
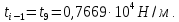
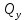
Полученные в характерных сечениях численные значения 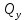без учёта сосредоточенной силы 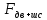, представлены в таблице 2.2.

Сосредоточенная сила 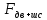от веса двигателя и шасси создает на эпюре 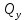скачок, величина и направление которого определяются в соответствии с правилом знаков метода сечений для построения эпюры поперечной силы, действующей в поперечных сечениях балки:

Численные значения поперечной силы в характерных сечениях с учётом сосредоточенной силы

---

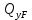
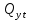
так же представлены в таблице 2.2. На рисунке 3.1, б показана эпюра 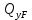с учетом сосредоточенной силы от веса двигателя и шасси .

Для получения эпюры изгибающих моментов эпюра 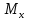поперечных сил вновь интегрируется: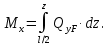

Интегрирование также ведется по методу трапеций:

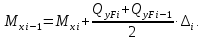
Результаты расчета 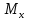представлены в таблице 2.2, графически на рисунке 3.1, в.



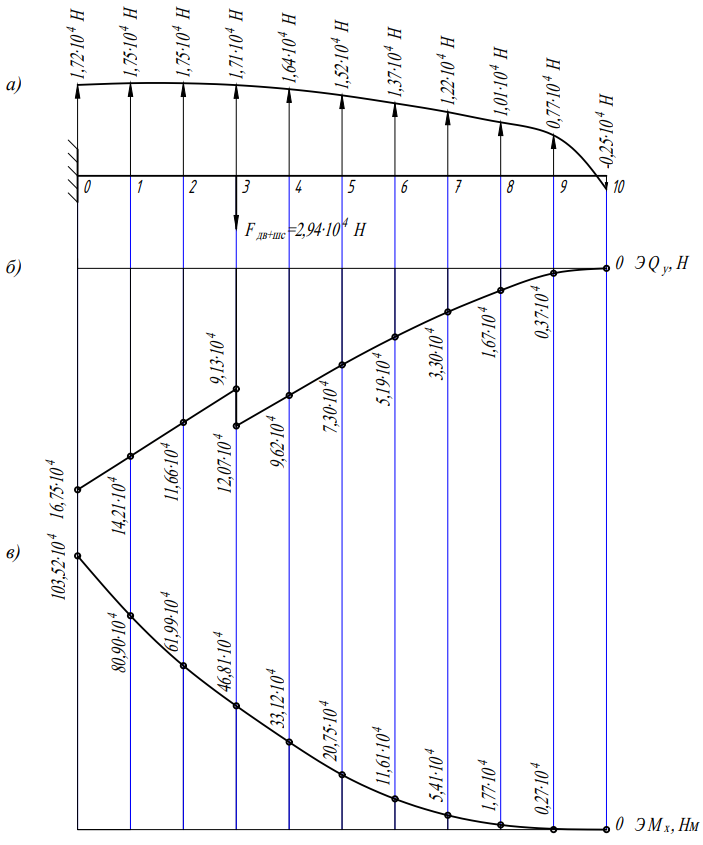
а) – расчетная схема крыла; б) – эпюра поперечной силы;

в) – эпюра изгибающего момента
Рисунок 3.1 – Эпюры внутренних силовых факторов



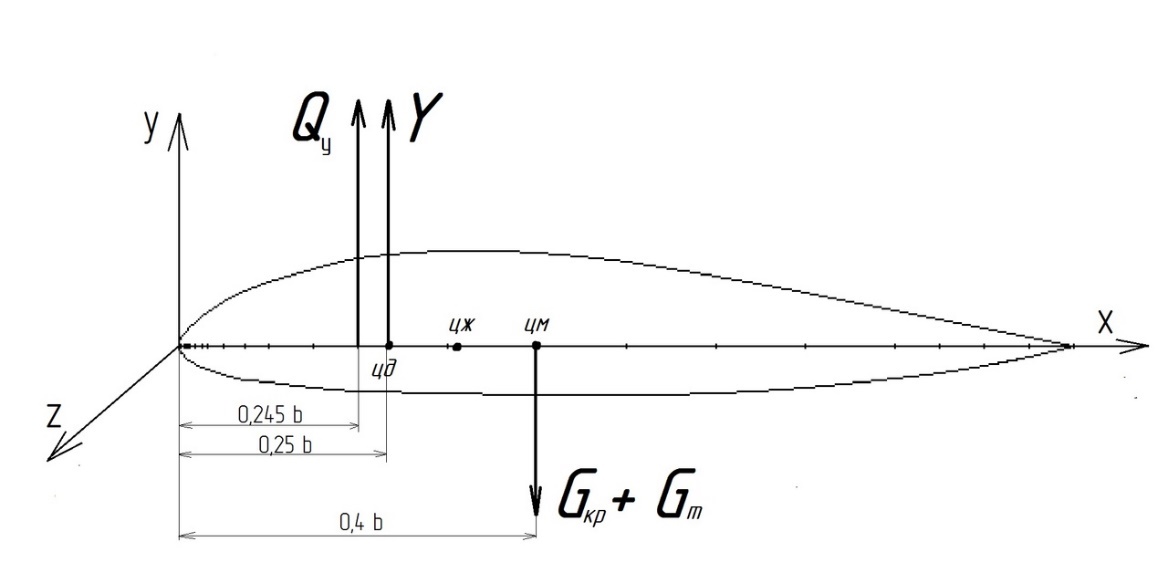
Для построения эпюры распределения крутящего момента 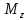по размаху крыла необходимо знать центр давления (точку приложения аэродинамической силы), центр массы конструкции крыла, центр массы топлива, размещенного в крыле (рисунок 7.1) и сосредоточенные моменты от агрегатов, закрепленных на крыле (главным образом двигателей).
Рисунок 3.2 – Абсциссы центра давления и центра масс сечения крыла
Введем допущение, что центр масс конструкции и центр масс топлива совпадают:



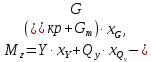
тогда абсцисса (при 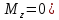определится так: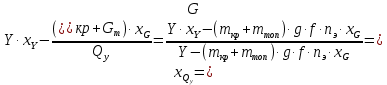




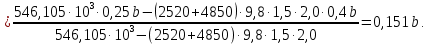
Расчеты для построения эпюры крутящих моментов представлены в таблице 3.1, а эпюра изображена на рисунке 4.2.

---

Таблица 3.1 – Расчет крутящего момента для полукрыла

i			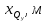Н∙104	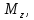Н∙м∙104	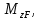Н∙м∙104
0	3,195	0,4835	19,6875	21,9314	21,1769
1	2,985	0,4518	17,1536	17,8551	17,1006
2	2,776	0,4201	14,5969	14,1270	13,3726
3	2,566	0,3884	12,0664	10,7963	10,0418
4	2,357	0,3566	9,6167	7,9016	7,9016
5	2,147	0,3249	7,3078	5,4704	5,4704
6	1,937	0,2932	5,1935	3,5082	3,5082
7	1,728	0,2615	3,3024	1,9894	1,9894
8	1,518	0,2298	1,6742	0,8862	0,8862
9	1,309	0,1980	0,3743	0,1708	0,1708
10	1,099	0,1663	0,0000	0,0000	0,0000

---

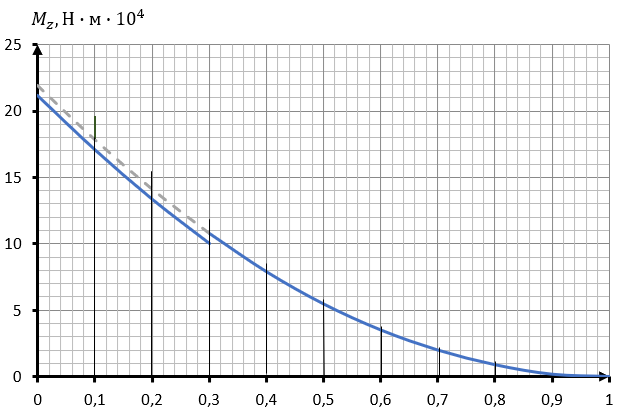
Рисунок 3.2 – Эпюра крутящего момента

---