Файл: Учебнометодическое пособие для выполнения лабораторных работ Волгоград, 2019 удк 519. 6(075. 8) Ббк в19я7 Печатается по решению редакционноиздательского совета Волгоградского государственного университета.docx

Задача 2.5. Найти приближенно корень уравнения f(x)=0, принадлежащий отрезку [a,b], с точностью , используя модификацию метода Ньютона для случая кратного корня при значениях m=1,2,3,4,5. По числу итераций определить кратность корня.Варианты заданий к задачам 2.1-2.5 даны в ПРИЛОЖЕНИИ 2.ПРИЛОЖЕНИЕ 2Таблица к задаче 2.1

N	f(x)	g(x)	[a, b]
2.1.1
2.1.2
2.1.3
2.1.4
2.1.5
2.1.6
2.1.7.			[5,25]
2.1.8			[0.1,10]
2.1.9			[0.1,2]
2.1.10
2.1.11
2.1.12
2.1.13			[0,3]
2.1.14			[0,2]
2.1.15			[0,3]
2.1.16
2.1.17
2.1.18
2.1.19
2.1.20
2.1.21
2.1.22			[0.001,3]
2.1.23			[0.1,35]
2.1.24			[0.01,3]
2.1.25
2.1.26			[-0.5,1.5]
2.1.27			[-1.5,0]
2.1.28			[1,3]
2.1.29			[0,3]
2.1.30			[0,5]

---

Таблица к задаче 2.2 Таблица к задаче 2.3

N	f(x)	Найти корень	N	f(x)
2.2.1		отрицательный	2.3.1
2.2.2		положительный	2.3.2
2.2.3		положительный	2.3.3
2.2.4		наибольший. по модулю	2.3.4
2.2.5		все корни	2.3.5

Таблица к задаче 2.4

f(x)
N
2.4.1	4.545004	-3.055105	-18.06895	4.002429	4.722482
2.4.2	-2.656764	-3.406111	10.89372	-1.752935	-3.423612
2.4.3	-4.556062	2.93309	9.274868	-10.32081	0.422098
2.4.4	7.809249	16.28542	-2.771356	-27.95304	-11.33921
2.4.5	-13.0072	60.24546	-122.0716	105.6798	-30.19201

---

Таблица к задаче 2.51   2   3   4   5   6

---

2.3 Лабораторная работа 3. « Интерполирование функций»

Цель: используя интерполяционную формулу, найти значение функции в точке, не являющейся табличной, и оценить погрешность метода решения; подобрать аналитическую формулу, представляющую с некоторой точностью данные табличные значения функции.Порядок выполнения работы

1. 
   Теоретическая часть
   

1.1 Основные определенияИнтерполяция - построение кривой, проходящей через контрольные точки.

Простейшая задача интерполирования заключается в следующем. На отрезке [A, b] заданы N+1 точки X0, x1, …, xn, которые называются узлами интерполяции, и значения некоторой функции F(X) в этих узлах: F(X0)=y0, f(X1)=y1, …, f(Xn)=yn. Требуется построить функцию F(X) (интерполирующую функцию), принадлежащую известному классу и принимающую в узлах интерполяции те же значения, что и F(X): F(X0)=y0, F(X1)=y1, …, F(Xn)=yn. Геометрически это означает, что нужно найти кривую Y=F(X) некоторого определенного типа, проходящую через заданную систему точек Mi(Xi, yi) (I=0, 1, 2, …, n) Функцию F(X) будем искать в виде полинома Pn(X) степени не выше N. Полученную интерполяционную формулу Y=F(X) обычно используют для приближенного вычисления значений данной функции F(X) в точках X, отличных от узлов интерполирования, при этом, если XÎ [X0, xn], то речь идет о задаче интерполирования, если XÏ [X0, xn] -экстраполирования.

Постановка задачи интерполяции: поиск такой функции F из заданного класса функций, что Точки x_i называют узлами интерполяции, а их совокупность - интерполяционной сеткой.  Пары (x_i ; y_i ) называют точками данных или базовыми точками.Разность между «соседними» значениями — шагом интерполяционной сетки. Функцию F(x) — интерполирующей функцией или интерполянтой.Виды интерполяций

---

:

1. Локальная – соединение точек отрезками прямой (по двум точкам), отрезками параболы (по трем точкам).

2. Глобальная – соединение всех точек f(x) единым интерполяционным полиномом.

Интерполяционный многочлен Лагранжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для n + 1 пар чисел х= x_i , где все x_i различны, существует единственный многочлен L(x) степени не более n, для которого L(x_i) = y_i.





Получаем непрерывную функцию, проходящую через все точки.

Минусы:

1. 
   Требует значительного объема вычислений для нахождения значения функции в произвольной точке.
   
2. 
   Неопределенное поведение построенной функции между узлами.
   

Будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке, что позволяет лучше учитывать локальное поведение требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).1.2 Интерполяционные формулы ньютона

• 
  конечные разностями первого порядка:  y_i = y_i+1 - y_i (i = 0, 1, 2, ...).
  
• 
  конечные разности второго порядка:  ²y_i =  y_i+1 -  y_i (i = 0, 1, 2, ...)
  
• 
  конечные разности третьего порядка:  ³y_i =  ²y_{i + 1} -  ²y_i = ( y_{i + 2} -  y_{i + 1}) - ( y_{i + 1} -  y_i) = ( y_{i + 3} - 2y_{i + 2} + y_{i + 1}) - (y_{i + 2} - 2y_{i + 1} + y_i ) =y_{i + 3} - 3y_{i + 2}+ 3y_{i + 1} - y_i
  
• 
  таблица конечных разностей:
  

x	y	 y	 y	 y	. ..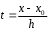
x	y	 y	 y	 y
x	y	 y	 y	 y
x	y	 y	 y	...
x	y	 y	...
x4	y4	...
...	...

---