Б. Одновременный двойственный симплекс-метод
1. Выражение базисных переменных ПЗЛП и ДЗЛП через свободные.

Выразим базисные переменные ПЗЛП и ДЗЛП через свободные:


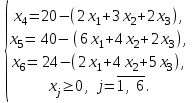
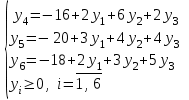
2.Определение исходного решения прямой и двойственной задач и проверка его на оптимальность.

Правила определения исходного решения прямой и двойственной задач и проверка его на оптимальность

Для этого заполняют симплекс-таблицу двойственного симплекс-метода. Таблица имеет два входа: по переменным прямой задачи x_j и по переменным двойственной задачи y_i. Базисные переменные ПЗЛП записывают в столбце x_баз, а свободные переменные в строке x_св со знаком «». Базисные переменные ДЗЛП записывают в строке у_баз, а свободные переменные в столбце у_св.

Строки таблицы 1-го шага (верхние части клеток) заполняют по данным системы ограничений и целевой функции прямой задачи. Столбцы таблицы 1-го шага (верхние части клеток) заполняют по данным системы ограничений и целевой функции двойственной задачи. Значение целевой функции равно нулю, поскольку базисные переменные не входят в выражение целевой функции.

Решение является оптимальным, если в строке и столбце b_i нет отрицательных элементов. В противном случае следует провести изменения в базисных переменных.
Симплексная таблица двойственного симплекс-метода для варианта 0 имеет следующий вид:

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	2	3	2	20
y2	x5	6	4	3	40
y3	x6	2	4	5	24
cj		- 16	- 20	- 18	0

---

Решение ПЗЛП выписывается по строкам, значения базисных переменных берутся из столбца b_i, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: = (0, 0, 0, 20, 40, 24), = 0.

Решение ДЗЛП выписывается по столбцам, значения базисных переменных берутся из строки c_j, если переменная с соответствующим индексом не входит в базис, то ее значение равно нулю: 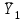= (0, 0, 0, 16, 20, 18), 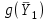= 0.

Данное решение не является оптимальным, поскольку решение не допустимое (не выполнено условие не отрицательности переменных), ему соответствуют отрицательные элементы в строке . Поэтому следует провести замену переменных в базисе.

3. Выбор разрешающей строки.

Правила выбора разрешающей строки

Находят отрицательный элемент в строке . В столбце над этим найденным элементом выбирают любой положительный элемент, эта строка – разрешающая.

Если в столбце над найденным элементом нет положительных элементов, то ПЗЛП не имеет смысла (целевая функция не ограничена в области допустимых решений), а ДЗЛП не имеет решения.
В рассматриваемом примере в строке три отрицательных элемента

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	2	3	2	20
y2	x5	6	4	3	40
y3	x6	2	4	5	24
cj		- 16	- 20	- 18	0

---

Можно выбрать любой из них, поэтому выбираем «20», а над ним выбираем элемент из первой строки «3». Следовательно, первая строка – разрешающая (выделена жирным шрифтом).
4. Выбор разрешающего столбца.
Правила выбора разрешающего столбца

Элементы строки делят на соответствующие элементы разрешающей строки под переменными. Из полученных отношений выбирают максимальное отрицательное отношение, этот столбец – разрешающий (максимальным из отрицательных отношений может быть отношение 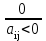– отрицательный ноль).

Если среди полученных отношений нет отрицательных, то ПЗЛП не имеет решения, ДЗЛП не имеет смысла или решения.

На пересечении разрешающей строки и разрешающего столбца находится разрешающий элемент.
В рассматриваемом примере максимальным среди отношений элементов из строки и элементов разрешающей строки является отношение во втором столбце 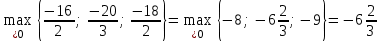. Следовательно, второй столбец – разрешающий (выделен жирным шрифтом).

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	2	«3»	2	20
y2	x5	6	4	3	40
y3	x6	2	4	5	24
cj		- 16	- 20	- 18	0
					-

---

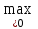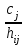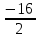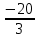Разрешающим элементом является элемент «3», который стоит на пересечении первой строки и второго столбца.

5. Заполнение нижних частей клеток таблицы.

Правила заполнения нижних частей клеток разрешающей строки

и разрешающего столбца

Под разрешающим элементом всегда ставят «1». Остальные элементы разрешающей строки переписываются без изменений, а остальные элементы разрешающего столбца переписываются с противоположным знаком.

Заполнение нижних частей клеток для разрешающей строки и разрешающего столбца варианта 0:

	yбаз	y4	y5	y6
yсв	xсв xбаз	- x1	- x2	- x3	bi
y1	x4	2 2	«3» 1	2 2	20 20
y2	x5	6	4 -4	3	40
y3	x6	2	4 -4	5	24
cj		- 16	- 20 20	- 18	0

6. Заполнение нижних частей для остальных клеток.

Правила заполнения нижних частей остальных клеток

Остальные элементы таблицы в нижних частях клеток находят по правилу прямоугольника: для искомого элемента из нижней части клетки элемент из верхней части этой же клетки умножают на разрешающий элемент и из этого произведения вычитают произведение элементов, расположенных на противоположной диагонали прямоугольника, образуемого искомым и разрешающим элементами (все элементы из верхних клеток).

---

Заполнение нижних частей для остальных клеток варианта 0:

клетка на пересечении второй строки и первого столбца:

2	«3»
6	4

63  24 = 10;

клетка на пересечении третьей строки и первого столбца:

2	«3»
	
2	4

23  24 = 2; клетка на пересечении четвертой строки и первого столбца:

2	«3»
	
- 16	- 20

---

Смотрите также файлы

• Повышение конкурентоспособности организации на рынке гигиенических продуктов (на примере ооо Эссити).pdf

• Практических заданий по дисциплине жанры мультимедиа.docx

• Задачи представленной работы, способствующие достижению цели.docx

• 1. Данные, определенным образом организованные, имеющие смысл, значение и ценность для своего потребителя и необходимые для принятия им решений, а также реализации других функций и действий, это .docx

• Частное профессиональное образовательное учреждение Гуманитарный колледж Эдельвейс задание.docx