Файл: Александры Анатольевны.doc

12345

7

6


?

Власовой

Александры Анатольевны

ОГЛАВЛЕНИЕ

	Стр.
I. Введение ……………………………………………….……………...…………………………………………………..	1
II. Основная часть 1. Теоретическое обоснование темы с позиции психологии и педагогики ……………………………………………….………………...……………………….……………………	3
Формирование активного, самостоятельного, творческого математического мышления (психологический аспект) …………………...	3
Использование методов проблемного обучения и идеи алгоритмизации обучения при изучении темы "Решение задач с параметрами" (педагогический аспект) ………………………………..…………….…… Проблемный метод …………………….…………………………….…………………………………..… Формирование алгоритмической культуры учащихся ………………...…………….. Интенсификация обучения …………………………………………………………………………….	6 6 8 9
2. Технология обучения решению задач с параметрами ……………………..…	10
3. Методические рекомендации и практический материал к теме "Решение задач с параметрами" в контексте программы по математике для 5-8 классов ……………………………………………………………………….……. 5-6 класс. Пропедевтика ………………………………………………………………....……………….....…. 7 класс. Линейные уравнения с параметрами ……………………...……………...…….……. 8 класс. Уравнения с параметрами, приводимые к линейным ..……………………. Линейные неравенства с параметрами ………………………...………………....… Квадратные уравнения с параметрами ………………….….…...……………..…… 9 класс. Квадратичная функция и ее график ……………………...……………...…...….…… Квадратные неравенства ………………….….…...……………..………………………….. Расположение корней квадратного трехчлена на числовой оси ……. Уравнения с одной переменной ..………………………………………………………..	16 16 20 29 38 43 54 56 60 66
III. Заключение ……………………………………………….…………………………………………………….….	68
IV. Литература ………………………………………………………………………………………………………...…	69

Введение
Математика учит точности мысли,

подчинению логике доказательства,

понятию строгого обоснования истины,

а все это формирует личность…

Александров А.Д.
Интеллектуальный уровень личности характеризуется двумя основными параметрами: объемом приобретенной информации и способностью использовать эту информацию для достижения определенных целей – для решения возникающих в процессе деятельности задач, разрешения различного рода проблемных ситуаций.

Первый из этих параметров характеризует эрудицию человека, второй – его интеллектуальное развитие.

Объем знаний, которые человек может усвоить в период школьного обучения, естественно, ограничен. Современной состояние науки и общества, увеличение объема новой информации резко сокращают долю знаний, получае-мых человеком в период школьного образования по отношению к информации, необходимой ему для полноценной деятельности в изменяющемся обществе.

В связи с этим на первый план выходит задача интеллектуального развития, и, прежде всего, таких его компонентов, как способность к усвоению новой информации, интеллектуальная подвижность, гибкость мышления.

Таким образом, основной задачей представляется переориентация методи-ческой системы обучения на приоритет развивающей функции обучения по отношению к его образовательной, информационной функции, перенос акцентов с увеличения объема информации на формирование умений использовать эту информацию, т.е. переход от экстенсивного школьного образования к интенсивному.

В настоящее время даже у школьников с ярко выраженными математическими способностями и живым интересом к математике – или, во всяком случае, у очень многих из них, – уровень общей математической культуры стал низким, познавательный аспект в их математических интересах в значительной степени вытеснен спортивным, а сама математика – компьютерами. Вдобавок эти школьники ориентированы на легкие пути приобретения знаний и имеют преувеличенное представление о своих достижениях.

В то же время совершенствование системы высшего образования неизбеж-но влечет за собой повышение требования к знаниям выпускника школы.

Современный уровень развития математики таков, что для получения высшего образования необходимы интенсивные, глубокие и непрерывные занятия на протяжении старших классов школы

Одной из наиболее сложных и важных тем является решение задач с параметрами.

Чтобы успешно справиться с ними, необходимо приобрести определенный опыт их решения, повысить уровень логической культуры. Между тем в средней школе (даже с углубленным изучением математики) решению таких задач уделяется недостаточно внимания. Более того, они представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков.

В настоящее время в учебной литературе появилось достаточно материала по этой теме, но, к сожалению, он разрознен, зачастую в публикациях рассматриваются частные примеры Все вышеизложенное побудило меня всерьез заняться разработкой данного вопроса в контексте программы по алгебре для основной школы, тем самым, расширив и углубив содержание некоторых основных тем курса.

Цель моей работы – научить школьников решать основные типы задач с параметрами, используя методы проблемного и программированного обучения, за счет интенсификации урока; формировать в процессе обучения активное, самостоятельное, творческое математическое мышление.

Теоретическое обоснование темы

с позиции психологии и педагогики.

Формирование активного, самостоятельного,

творческого математического мышления

(психологический аспект).
Человек, желающий стать математиком, с первых шагов должен любить и ценить красоту мысли, стройность выводов и построений, часто неожиданных и сильных.

Соболев С.Л.
Одними из целей школьного математического образования являются следующие:

• 
  формирование и развитие качеств мышления, необходимых образованному человеку для полноценного функционирования в современном обществе, в частности, формирование эвристического и алгоритмического мышления;
  
• 
  формирование и развитие абстрактного мышления и, прежде всего, его дедуктивной составляющей как специфической для математики.
  

Задачи с параметрами играют огромную роль в формировании математического и логического мышления.

А.Я. Хинчин, известный математик, глубоко интересовавшийся проблемами обучения математике и много сделавший в области методики математики, указал четыре характерных признака математического мышления:

1. 
   "Для математики характерно доведенное до предела доминирование логической схемы рассуждения… Эта своеобразная черта стиля математического мышления, в столь полной мере не встречающаяся ни в одной другой науке, имеет в себе много ценного. Очевидно, что она в максимально степени позволяет следить за правильностью течения мысли и гарантирует от ошибок; с другой стороны, она заставляет мыслящего иметь перед глазами всю совокупность имеющихся возможностей и обязывает его учесть каждую из них, не пропуская ни одной.
   
2. 
   "… лаконизм, сознательное стремление всегда находить кратчайший ведущий к данной цели логический путь, беспощадное отбрасывание всего, что не абсолютно необходимо для безупречной аргументации".
   
3. 
   "… четкая расчлененность хода аргументации". Для этого в математических работах широко используется такой простой прием, как нумерация понятий и суждений, а перед каждым абзацем ставится особое обозначение, указывающее, какой случай из всех рассматривается в данном абзаце.
   
4. 
   Скрупулезная точность символики. "Каждый математический символ имеет строго определенное значение, замена его другим символом или перестановка на другое место, как правило, влечет за собой искажение, а подчас и полное уничтожение смысла данного высказывания.
   

Все эти качества реализуются при решении любой задачи с параметрами.

Математическое мышление является составной частью общей культуры мышления, воспитание которой есть важнейшая задача общего образования.

Культура мышления отличается рядом признаков, среди которых в первую очередь следует выделить разумность, логичность и дисциплинированность.

Разумное мышление – это "способность находить причины и сущность явлений, рассматривать их всесторонне, вскрывать единство противоположностей" (философский словарь, М., 1972, стр. 346).

Важным качеством мышления является его логичность, т.е. способность делать из правильных посылок правильные выводы, находить правильные следствия из имеющихся фактов. Это ценнейшее качество возникает и развивается главным образом в процессе изучения математики, ибо математика – это практическая логика.

Дисциплина мышления предполагает, во-первых, анализ объекта мысли, во-вторых, планирование на основе этого анализа своей мыслительной деятельности, и, в-третьих, пошаговый самоконтроль и самооценку выполненной деятельности с целью установления соответствия намеченному плану и его корректировки при необходимости.

Воспитание культуры мышления должно проводиться повседневно. Кратковременное обучение логическим понятиям не дает заметного эффекта. Эти понятия органически вплетены в курс темы "Задачи с параметрами", поэтому решение таких упражнений оказывается очень эффективным для решения проблемы формирования логического мышления.

Решение параметрических задач развивает и способность догадываться, предполагать заранее результат, способность разумно искать правильный путь в самых запутанных условиях. Прочтя задачу и еще не производя никаких действий, ученик сразу видит, что тот или иной способ непригоден для ее решения, а вот какой-то другой способ может быть использован.

Выдающийся отечественный математик-педагог В.Л. Гончаров писал: "Тот, кто говорит только о логике, недооценивает роль интуиции. Математическая беспомощность учащихся есть прямой продукт подавления интуиции. Интуиция в математике есть вырабатываемая в процессе обучения способность находить ответы на вопросы и ускоренно выполнять логические построения, базирующиеся на принципе моделирования (по большей части ясно не осознанном)".

Учитывая возрастные особенности подросткового и юношеского возраста, я считаю вполне обоснованным знакомить с параметрами учащихся, начиная с 5 класса.

В этом возрасте активно идет процесс познавательного развития. Подростки и юноши уже могут мыслить логически, заниматься теоретическими рассуждениями. Учащиеся могут формулировать гипотезы, рассуждать предположительно, исследовать и сравнивать между собой различные альтернативы при решении одних и тех же задач.

Мышление подростка характеризуется стремлением к широким обобщениям.

По исследованиям Ж. Пиаже на рубеже 10-12 лет умственная деятельность ребенка не ограничена его опытом. Он может мысленно представлять возможные случаи и события, делать выводы о потенциальных отношениях, приобретает способность к формальному выражению конкретных идей.

Примерно к 14-15 годам у него формируется логика взрослого человека.

На основании этого можно утверждать, что учащиеся 12-13 лет психологически созрели для рассмотрения предъявленной темы.

Использование методов проблемного обучения

и идеи алгоритмизации обучения

при изучении темы "Решение задач с параметрами"

(педагогический аспект).
Проблемный метод
Для всех математиков характерна дерзость ума.

Математик не любит, когда ему о чем-нибудь

рассказывают, он сам хочет дойти до всего.

Сойер У.
Мыслить человек начинает, когда у него появляется потребность что-то понять. Мышление обычно начинается с проблемы или вопроса, с удивления или недоумения, с противоречия.

Знания в значительной своей части не передаются учащимся в готовом виде, а приобретаются или в процессе самостоятельной познавательной деятельности в условиях проблемной ситуации.

Проблемное обучение заключается в создании перед учащимися проблемных ситуаций, осознании, принятии и разрешении этих ситуаций в процессе совместной деятельности учащихся и учителя при максимальной самостоятельности первых и под общим руководством последнего, направляющего деятельность учащихся.

Проблемное обучение способствует реализации двух целей:

1. 
   сформировать у учащихся необходимую систему знаний, умений, навыков;
   
2. 
   сформировать особый стиль умственной деятельности, исследовательскую активность и самостоятельность учащихся.
   

Проблемная ситуация характеризует определенное психологическое состояние учащегося, возникающее в процессе выполнения задания, для которого нет готовых средств и которое требует усвоения новых знаний о предмете, способах или условиях выполнения задания.

Для создания проблемной ситуации перед учащимися должно быть поставлено такое практическое или теоретическое задание, при выполнении которого они должны открыть подлежащие усвоению новые знания. Задание основывается на тех знаниях и умениях, которыми владеют ученики. Неизвестное, которое нужно открыть, составляет подлежащую усвоению общую закономерность, общий способ действия или некоторые общие условия выполнения действия. Следует учесть, что ни слишком трудное, ни слишком легкое задание не вызовет проблемной ситуации, поэтому предлагаемое задание должно соответствовать интеллектуальным возможностям учащихся.

Принято различать четыре основных звена процесса проблемного обучения:

1. 
   осознание общей проблемной ситуации;
   
2. 
   анализ ее, формулировка конкретной проблемы;
   
3. 
   решение проблемы (выдвижение, обоснование гипотез, последовательная проверка их);
   
4. 
   проверка правильности решения проблемы.
   

Безусловно, проблемный метод нельзя превращать в универсальный метод обучения. Для некоторых учащихся он несколько труден. Да и времени он требует больше, чем традиционное информационно-сообщающее изложение. Поэтому я использую проблемный метод дозированно, если уверена в успехе его применения.

формирование

алгоритмической культуры

учащихся.
Высшее назначение математики…

состоит в том, чтобы находить

скрытый порядок в хаосе,

который нас окружает.

Винер Н.
Курс темы "Решение задач с параметрами" имеет достаточно широкие возможности формирования, изучения и применения алгоритмов, т.к. в его содержании естественным образом закладывается алгоритмическая линия.

Выявление или построение в содержании и в процессе обучения алгоритмов и представление их в какой-либо форме пошаговой программы деятельности учения называется алгоритмизацией обучения.

В содержании обучения решению параметрических задач необходимо явно выделять учебные алгоритмы (предписания).

Учебные алгоритмы служат предметом усвоения для учащихся, а зачастую и средством обучения, показывающим, какие действия и в каком порядке должны выполнять учащиеся, чтобы усвоить соответствующее знание.

Психологическое значение алгоритмизации обучения состоит в том, что она способствует явному различению учащимися содержательной и операционной сторон изучаемых знаний и овладению общим способом решения широкого класса задач.

Кроме того, ориентация обучения по линии алгоритмической направленности дает новую возможность существенно разнообразить виды учебной деятельности учащихся, наполняет ее более конкретным содержанием, влияет на изменение организационных форм проведения уроков.

При составлении алгоритмов требуется:

1. 
   выделить все шаги алгоритма и действия учащихся для выполнения каждого из них;
   
2. 
   выполнить необходимые теоретические обоснования;
   
3. 
   продумать письменное оформление реализации алгоритма;
   
4. 
   выбрать методы самоконтроля;
   
5. 
   отобрать задачи для формирования у учащихся умений реализовать алгоритм.
   

интенсификация

обучения
Дороги не те знания, которые

отлагаются в мозгу, как жир;

дороги те, которые превращаются

в умственные мышцы.

Спенсер Г.
Учитывая ограниченные временные рамки, отведенные на изучение отдельных вопросов программы, встает проблема интенсификации обучения. В основу такого обучения положены следующие принципы:

1. 
   построение обучения на высоком уровне трудности (при строгом соблюдении меры трудности!). Только такое обучение, которое дает пищу для напряженной умственной работы, может содействовать быстрому и интенсивному развитию учащихся;
   
2. 
   прохождение материала быстрым темпом (опять-таки в разумных пределах);
   
3. 
   резкое повышение удельного веса познавательной стороны обучения, теоретических знаний.
   

Следует опасаться "недогрузить" мозг, чем "перегрузить" его. А "недогрузить" мозг – не всегда значит только чуть замедлить его развитие, это чаще всего означает привести школьника к ограниченности мышления, к привычке мыслить избитыми шаблонами, к отказу от всего нового, творческого.

Л.С. Выгодский говорит, что обучение должно ориентироваться не на уже достигнутый учеником уровень развития, а немного забегать вперед, предъявляя к мышлению школьника требования, несколько превышающие его наличные возможности.

В содержании темы "Решение задач с параметрами" кроме системы знаний, следует предусмотреть особые типы познавательных задач, которые помогут не только более сознательному усвоению вопроса, но и развитию способности самостоятельно добывать и применять знания, творчески мыслить и действовать.


технология обучения

решению задач с параметрами

Математическая истина только тогда

должна считаться вполне отработанной,

когда она может быть объяснена

всякому из публики, желающему ее усвоить.

Жуковский К.Е.
Известно, что в программах по математике задачам с параметрами отводится незначительное место. Поэтому, в первую очередь, укажем разделы общеобразовательной математики, в которых вообще присутствует сама идея параметра:

• 
  Функция прямая пропорциональность: y = kx
  

(x, y – переменные, k – параметр, k  0)

• 
  Линейная функция: y = kx + b
  

(x и y – переменные, k и b – параметры)

• 
  Линейное уравнение: ax + b = 0
  

(x – переменная, a и b – параметры)

• 
  Уравнение первой степени: ax + b = 0
  

(x – переменная, a и b – параметры, a  0)

• 
  Линейное неравенство
  

• 
  Квадратное уравнение: ax2 + bx + c = 0
  

(x – переменная, a, b, c – параметры, a  0)

• 
  Квадратичная функция: y = ax2 + bx + c
  

(x и y – переменные, a, b, c – параметры)

• 
  Квадратные неравенства
  

В содержание каждой названной темы включается блок материала, связанный с параметром.

При методической разработке этого блока выделяются следующие шаги:

1. 
   Изучение программы и учет "требований жизни".
   
2. 
   Анализ учебного материала.
   
3. 
   Методы решения и составления задач по теме.
   
4. 
   Выбор алгоритмов решения типовых задач.
   

В первую очередь следует определить вопросы теории, знания и умения, которые должны быть сформированы у всех учеников; число часов, отводимое на изучение темы.

Успех работы над темой во многом зависит от того, как удается учесть "требования жизни". В любом классе имеется значительное число учащихся, которые готовятся поступать в институты, где требуется серьезная математическая подготовка.

При отборе материала учитывается подготовка учащихся класса, результаты работы по предыдущим темам. На основе этого учитель определяет материал для повторения.

Затем необходимо уточнить затраты времени на изучение темы в целом и по отдельным урокам, определить содержание материала предстоящей лекции.

Весь материал рассортировывается. Главная часть – тот материал, который будет изучаться на уроках, далее – материал для занятий факультатива, индивидуальных заданий, специальный материал для работы со старшеклассниками.

Под "главным содержанием" понимается та часть материала, без усвоения которой не могут быть решены задачи изучения темы.

Определив главное, надо выбрать психологически правильную линию поведения, которая заставит ребят самостоятельно определить метод решения, установить особенности задачи, систематизировать материал.

Далее можно приступить к прогнозированию затруднений учащихся и возможных типичных ошибок.

Для выявления затруднений учащихся желательно изучить требования к учащимся к овладению общеучебными умениями. Это позволяет:

а) выявить навыки учебного труда, которые не сформированы у уча-щихся, но им необходимы;

б) установить, какие из общеучебных умений можно продолжить фор-мировать при работе над темой;

в) определить наличие в системе упражнений задания для формирова-ния общеучебных умений;

г) спрогнозировать возможность самостоятельного изучения отдельных частей материала.

На следующем шаге методической разработки важно повторить и систематизировать методы решения задач по этой теме. Для этого требуется:

а) выделить типы задач;

б) определить методы решения этих задач;

в) продумать методику знакомства учащихся с избранными методами решения.

При решении задач с параметрами преимущественно применяются два метода: графический и аналитический.

При выделении методов решения задач по теме следует помнить, что сложная задача чаще всего имеет единственный метод решения.

Важна работа и по составлению задач. Методы составления задач могут быть такими:

1. 
   Берется какой-либо пример, конструкция которого сохраняется, но вносятся изменения в числовые данные или в требование задачи, либо одновременно.
   

Пример: 1) Исходное задание.

При каких значениях параметра aуравнение x² (3a 1) x + 2a²a = 0 имеет четыре различных решения?

 x² (3a 1) x+ 2a²a = 0,

  x= 2a 1,

 x= a.

Для того чтобы исходное уравнение имело четыре решения, необходимо, чтобы каждое уравнение совокупности имело два различных решения, и они не совпадали.

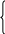
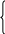a  0, a  0,

2a  1  0, a  ,

a  2a  1; a  1.

Ответ: ( ; 1) U (1; ).

2) Изменим задание.

При каких значениях параметра b уравнение x² (4b 2) x + 3b² 2b = 0 имеет два различных решения?

 x² (4b  2)  x + 3b² 2b = 0;

 x² (3b  2 + b)  x + (3b  2)b = 0;

  x = 3b  2,

 x = b.

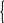
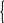
 b  0,  b  0, b  0,

3b  2  0; b  ;

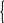
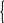b  0, b  0, 0  b  ,

3b  2  0; b  ;

 b = 3b  2  0,  b  1 0,  b = 1.

Ответ: (0; ) U 1.

2. 
   В известных примерах числовые данные заменяются параметрами.
   

Пример: В исходном примере: решить уравнение х = 2 – выделяется число 2, которое может быть заменено параметром. Получим: х = a. Решение последнего уравнения содержит элементы исследования, так как нужно учесть условие a  Z, вспомнив определение целой части.

3. 
   Составление уравнения, решаемого тем же приемом, что и исходное:
   

Пример: Исходное уравнение: (x²a) ² 6x²+4x + 2a = 0. (1)

1) Рассмотрим данное уравнение как квадратное относительно a.

x⁴ 2ax² + a² 6x²+4x + 2a = 0;

a² 2 (x² 1) a + x⁴ 6x² + 4x = 0;

a_1,2 = x² 1  x⁴ 2x² + 1  x⁴ + 6x² 4x ;

a_1,2 = x² 1  4x² 4x + 1 ;

a_1,2 = x² 1  (2x 1) (2)

Таким образом, уравнение (1) распадается на два квадратных уравнения относительно x:

x² + 2x  a – 2 = 0 x² 2x – a = 0

x_1,2 = 1  a + 3 x_3,4 = 1  a + 1

Ответ: при a3 корней нет;

при a = 3 x = 1;

при 3  a 1 x_1,2 = 1  a + 3;

при a = 1 x₁ = 1  2, x₂ = 1 +  2, x₃ = 1;

при a 1 x_1,2 = 1  a + 3, x_3,4 = 1  a + 1

2) Рассматривая этапы решений уравнения (1) с конца, видно, что следует начинать с составления выражения вида (2):

b_1,2 = x² + 2  (3x 1).

Далее запишем два квадратных уравнения с параметром b:

x² + 3xb + 1 = 0; x² 3xb + 3 = 0.

Перемножив левые части этих уравнений, получим уравнение четвертой степени относительно x:

x⁴ (5 + 2b) x² + 6x + b² 4b + 3 = 0,

(x² b)² 5x² + 6x  4b + 3 = 0.

Решается так же, как уравнение (1).

4. 
   Составление задач, обратных данным.
   

Пример 1.

1) Дано уравнение первой степени 5x 2a = ax 3.

Требуется определить область изменения параметра a, если данное уравнение имеет решение: 2 x 8.

Ответ: 3,25  а  4,3.

2) (Обратная задача). В уравнении 5x 2a = ax 3 параметр a изменяется на промежутке 3,25  а  4,3. Определить соответствующую область изменения значений корня.

Пример 2.

1) Пусть решена следующая задача на неравенства:

В каком промежутке должно изменяться число a, чтобы оба корня уравнения

x² 2ax + a² 1 = 0 были заключены между 2 и 4 ?

Ответ: 3  а  5.

2) (Обратная задача). Дано уравнение x² 2ax + a² 1 = 0. В каких пределах будут изменяться корни уравнения, если параметр a изменяется в пределах

3  а  5 ?

Умение решать прямую и обратную задачи является важным критерием достигнутой учеником глубины понимания изучаемого раздела математики, развития творческого мышления, одним из путей саморазвития ума учащихся.

При выборе метода следует продумать такие моменты:

1. 
   Идея метода.
   
2. 
   Выбор примера для первого знакомства.
   
3. 
   Способ выполнения анализа условия с целью определения метода решения.
   
4. 
   Возможности самоконтроля.
   
5. 
   Методы усложнения заданий.
   
6. 
   Подготовка банка заданий.
   
7. 
   Стереотипы мышления, которые мешают при реализации метода и способы их преодоления.
   

Когда закончена методическая разработка темы, следует переходить к составлению лекции для учащихся. Очевидны следующие требования к школьной лекции:

1. 
   Лекция должна быть интересной для учащихся и для учителя.
   
2. 
   Научный уровень лекции должен соответствовать уровню развития учащихся класса.
   
3. 
   Лекция должна быть обучающей, развивающей и воспитывающей.
   
4. 
   Тема лекции должна естественным образом вытекать из ранее изученного и прокладывать тропинку к последующему.
   
5. 
   Лекция должна быть совместным делом учащихся и учителя.
   
6. 
   Лекция должна быть емкой, целостной, размерной, ритмичной, обстоятельной.
   
7. 
   Главные мысли должны быть повторены несколько раз, выписаны аккуратно на доске и законспектированы учениками.
   

Специальные графические средства (подчеркивание, выделение) помогают представить конспектируемый материал в наиболее запоминающейся форме.

Основная часть лекции сопровождается вопросами к классу "А как вы думаете?" и т.п. Такие вопросы стимулируют учащихся к активной работе на лекции, помогают им не "выключаться" из процесса познания.

Одно из главных правил – на лекции должны быть вопросы, т.к. способность задавать вопросы является верным признаком активной мыслительной деятельности.

Для урока решения ключевых задач выбираются задачи, соответствующие следующим критериям:

1. 
   Соответствие данной теме.
   
2. 
   Степень использования при изучении последующих тем.
   
3. 
   Затраты времени по обучению учащихся решению задач.
   
4. 
   Оптимальность алгоритмов решения задач.
   
5. 
   Возможность поразить учащихся красотой решения.
   

Способ выделения ключевых задач основан либо на умениях, которые должны быть сформированы у учеников после изучения темы, либо на методах решения задач по изучаемой теме.

При определении последовательности ключевых задач учитываются следующие рекомендации:

1. 
   Начинать лучше всего с самых простых ключевых задач.
   
2. 
   Те ключевые задачи, которые связаны с предыдущей темой, включать в число первых, а используемые в последующих темах разбирать позднее.
   
3. 
   Самые красивые задачи отнести на вторую часть урока.
   
4. 
   Чередовать задачи, требующие обширных записей, с теми, которые не требуют громоздких обоснований.
   

При разборе решений ключевых задач лучше обратиться к лекции. "Размышляя вслух", учитель знакомит ребят с логическими приемами, на основе которых выбирается тот или иной подход к решению. Для того, чтобы убедиться, что учащиеся поняли, можно обратиться к конкретному ученику с предложением рассказать решение ключевой задачи.

К основным задачам урока решения обучающих задач можно отнести:

• 
  ознакомление школьников с решениями задач, сводящихся к решению ключевых;
  
• 
  систематизацию методов решения задач по теме;
  
• 
  обучение решению задач по теме в ходе специальных упражнений.
  

В планируемой системе обучающих задач должны быть представлены:

• 
  задачи на распознавание (т.е. задачи, в которых следует распознать ту или иную ключевую задачу);
  
• 
  задачи на реализацию методов;
  
• 
  задачи на применение (в них отрабатываемая задача служит вспомогательной при решении другой задачи).
  

Успех урока зависит от таких факторов:

• 
  соответствует ли система обучающих задач особенностям класса;
  
• 
  правильно ли организована работа по систематизации;
  
• 
  известны ли затруднения учеников.
  

В связи с тем, что программой не отведено специальное время на решение задач с параметрами, практикуются долгосрочные домашние задания. Обычно срок выполнения – 7-10 дней. По окончании этого срока на стенде в кабинете вывешивается решение предложенных задач, на текущем уроке делается краткий анализ домашнего задания, назначаются консультанты. Тема развивается по спирали, пронизывая программный материал, поэтому задачи с параметрами включаются либо последним номером в текущую самостоятельную или контрольную работу, либо как дополнительная задача. В течение года учащимся предлагается выполнить несколько проверочных работ, проверяющих навыки решения ключевых задач, а также домашняя контрольная работа, в которую уже включены задачи разной степени сложности. В конце года проводится итоговая контрольная работа
3. Методические рекомендации и практический материал к теме "Решение задач с параметрами"

в контексте программы по математике

для 5-8 классов

Преподавание алгебры должно усилить элемент рассуждений и обоснования правил в противовес часто наблюдаемой склонности к рецептуре. Соболев С.Л.
5-6 класс. Пропедевтика.

Несмотря на то, что в обучении математики в 5-6 классах встречаются буквенные выражения с одной или несколькими буквами (в частности, в вычислениях по формулам, при записи свойств арифметических действий), в упражнениях, направленных на отработку навыков преобразования буквенных выражений, решения уравнений и т.п., как правило, рассматриваются выражения лишь с одной буквой. Поэтому в самом начале знакомства с параметром (термин дается без определения; записывается на доске и в тетрадях учащихся, включается в словарную работу) у учеников возникает некий психологический барьер, который обусловлен противоречивыми характеристиками параметра. С одной стороны, параметр в уравнении, неравенстве, следует считать величиной известной, а с другой – конкретное значение параметра неизвестно. С одной стороны, параметр является величиной постоянной, а с другой – он может принимать различные значения. Получается, что параметр в уравнении – это неизвестная известная, переменная постоянная величина. Этот "каламбур" очень точно отражает существо тех сложностей, которые нужно преодолеть ученикам. Учитель должен не спеша, скрупулезно и обязательно доброжелательно разъяснить младшим школьникам такой сложный вопрос, обильно сопровождая его различными примерами.

Мне представляется целесообразным включать как в устные, так и в письменные упражнения задачи такого содержания:

5 класс

Тема "Натуральные числа"

1. 
   Сравните а и а + 3.
   
2. 
   Известно, что а  b. Расположите в порядке возрастания числа:
   

a + 8, b  4, a + 3, a, b  1, b.

3. 
   Зная, что а  b, сравните числа: а) 5 + a и b; б) b  8 и a;
   

в) 12a и 10b; г) 6a и b.

Очевидно, что данные задания решаются учениками 5 класса интуитивно, так как им не известны свойства неравенств, однако они развивают абстрактное мышление, столь необходимое математику.

Можно попросить проиллюстрировать свое утверждение на конкретных значениях a и b.