ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 136
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(m 1) f(2) 0, (m 1)(3m 12) 0, 1 m 4,
(m 1) f(4) 0; (m 1)(11m 32) 0; 1 m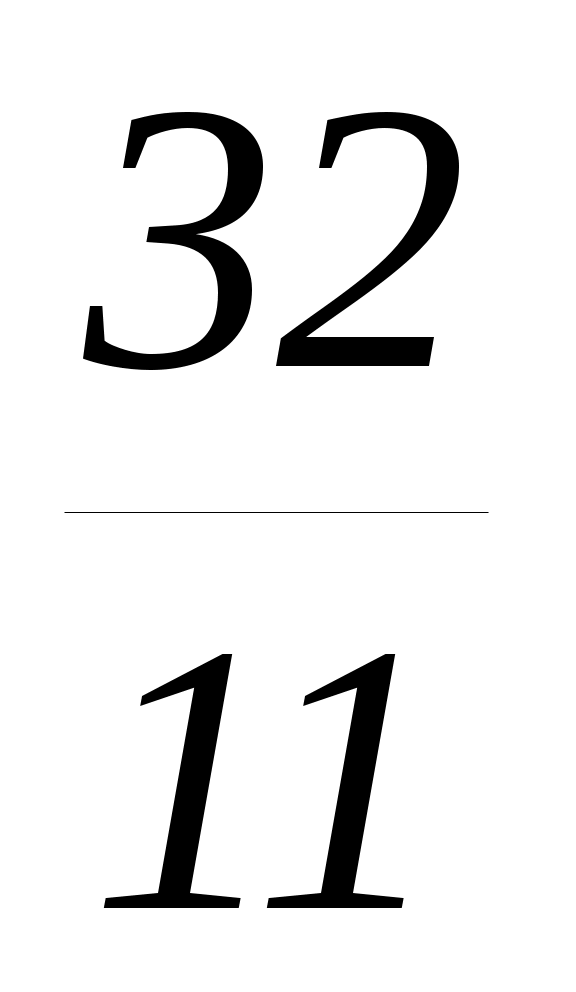 ;1 m
;1 m 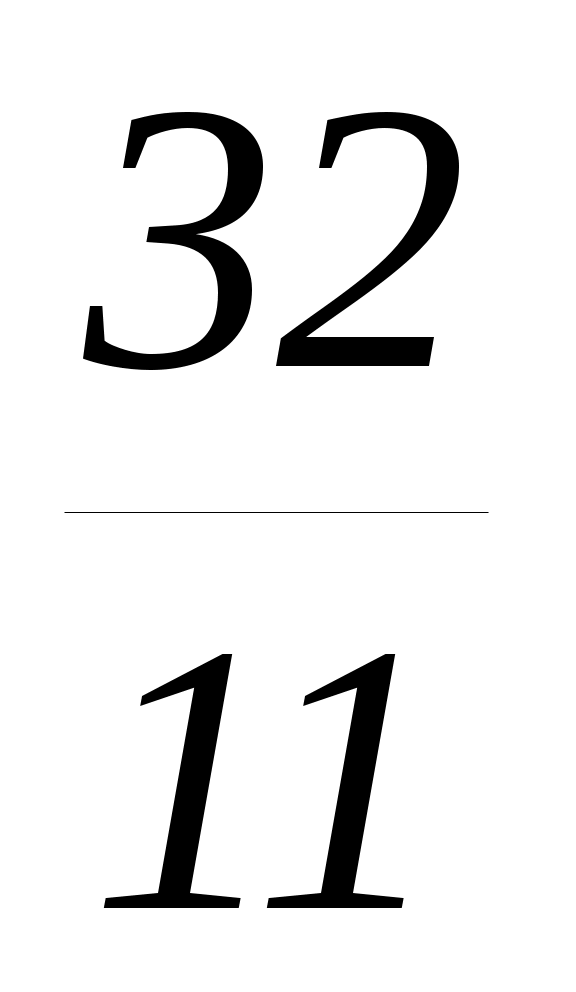 .
.
Ответ: (1;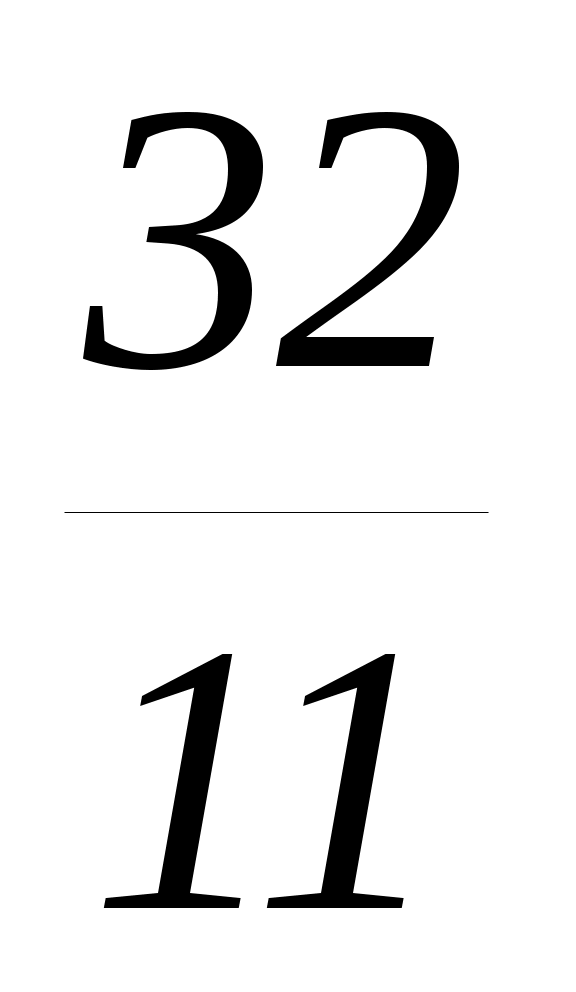 ).
).
Решение: Интервал (0; 2) должен содержаться во множестве решений данного неравенства, следовательно, должно выполняться соотношение
х1 0 2 х2
 f(0) 0, a2 6a 0, 0 a 6, 2 a 6.
f(0) 0, a2 6a 0, 0 a 6, 2 a 6.
f(2) 0; 4 + 4(a 3) + a2 6a 0; 2 a 8;
Ответ: [2; 6].
У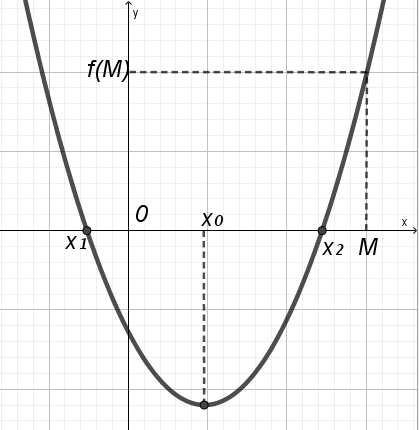 тверждение 3. Для того, чтобы оба корня квадратного трехчлена были меньше числа M (х1х2M), необходимо и достаточно выполнение условий:
тверждение 3. Для того, чтобы оба корня квадратного трехчлена были меньше числа M (х1х2M), необходимо и достаточно выполнение условий:
D 0;
0;
x0M;
А f(M) 0.
Доказательство.
(x1M) 0; (x2M) 0;
(x1M)(x2M) 0;
M2 (x1 + x2)M + x1 x2 0;
M2 + M +
M + 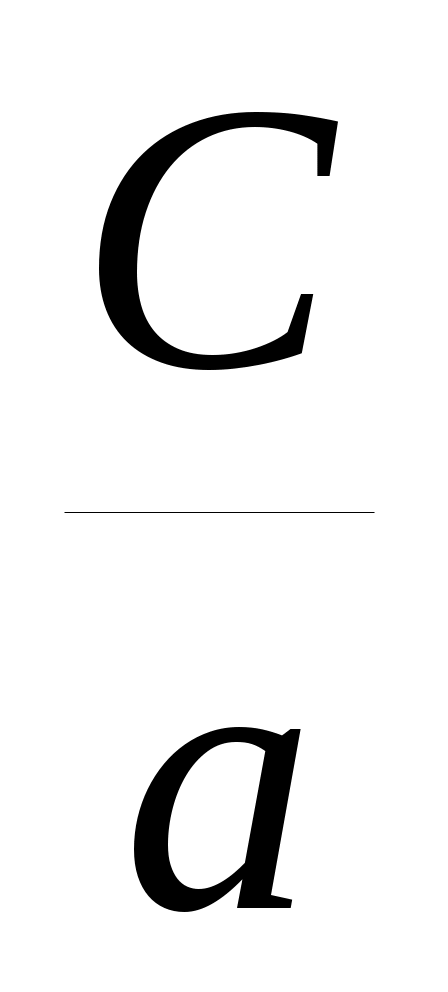
0 xa2;
a(aM2 + BM + C) 0;
af(M) 0.
У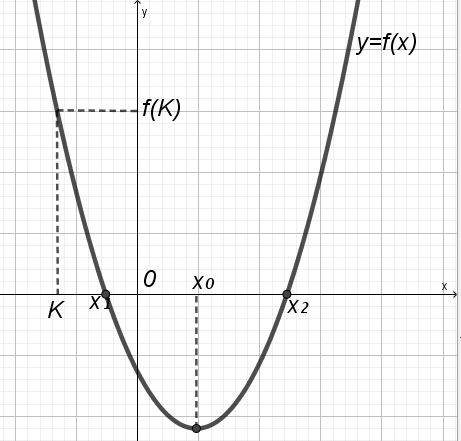 тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (Kх1х2), необходимо и достаточно выполнение условий:
тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (Kх1х2), необходимо и достаточно выполнение условий:
D 0;
0;
x0K;
А f(K) 0.
а) больше 1; б) меньше 1?
Р
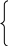 ешение: а) D 0, (3m + 1)2 4(2m2 + 4m 6) 0, (m 5)2 0,
ешение: а) D 0, (3m + 1)2 4(2m2 + 4m 6) 0, (m 5)2 0,
x0 1,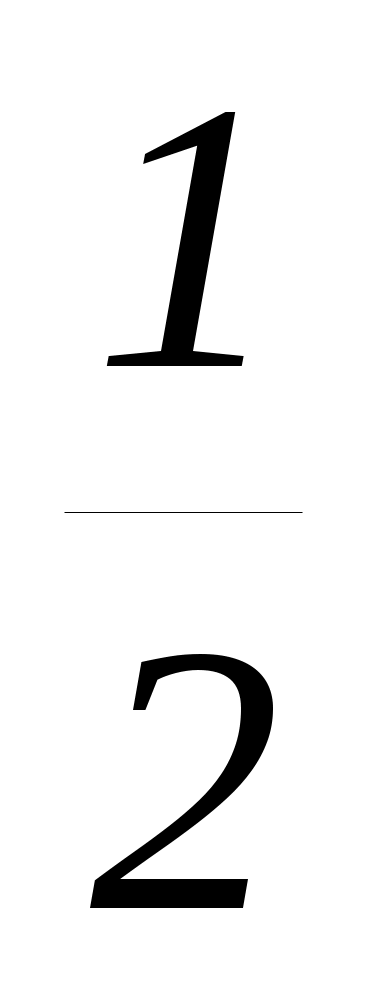 (3m + 1) 1, m
(3m + 1) 1, m 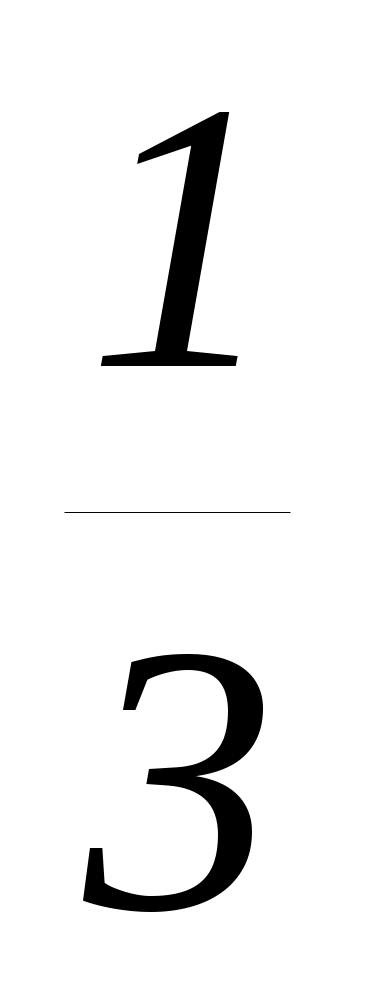 ,
,
f(1) 0; 1 (3m + 1) + (2m2 + 4m 6) 0; (2m 3)(m + 2) 0;
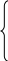 mлюбое число,
mлюбое число,
m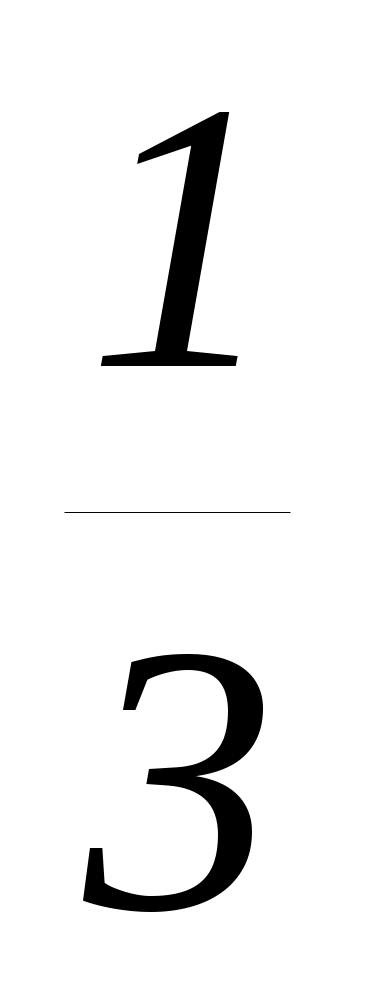 , m
, m 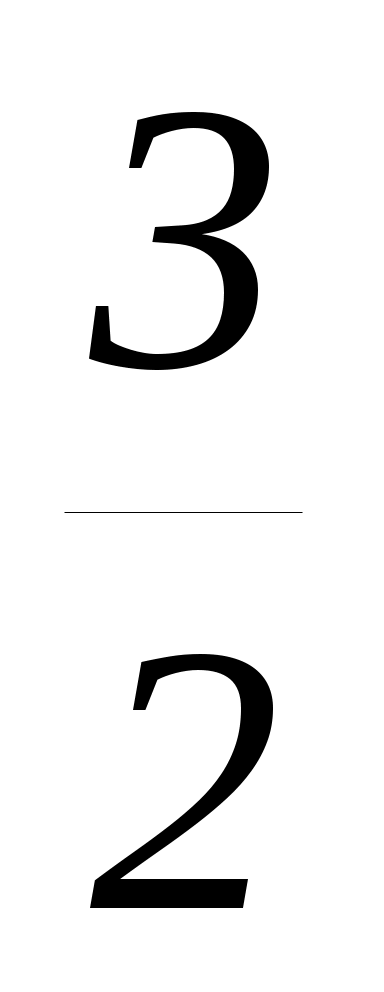 .
.
 m2,
m2,
m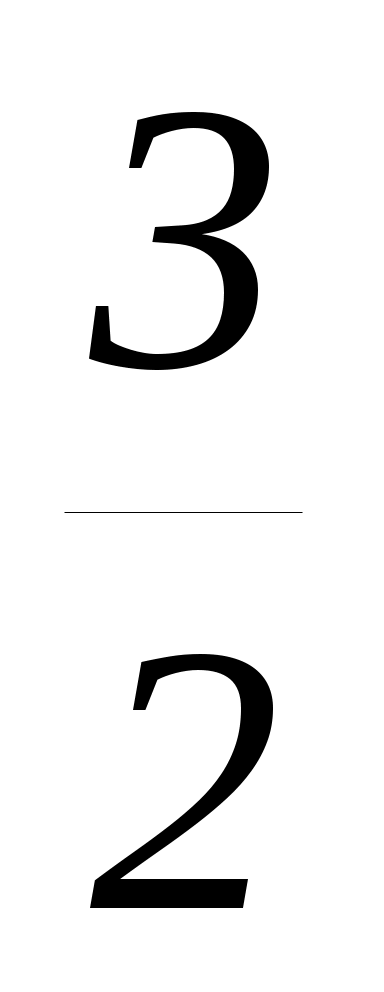 ;
;
б
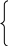 ) D 0, mлюбое число,
) D 0, mлюбое число,
x01,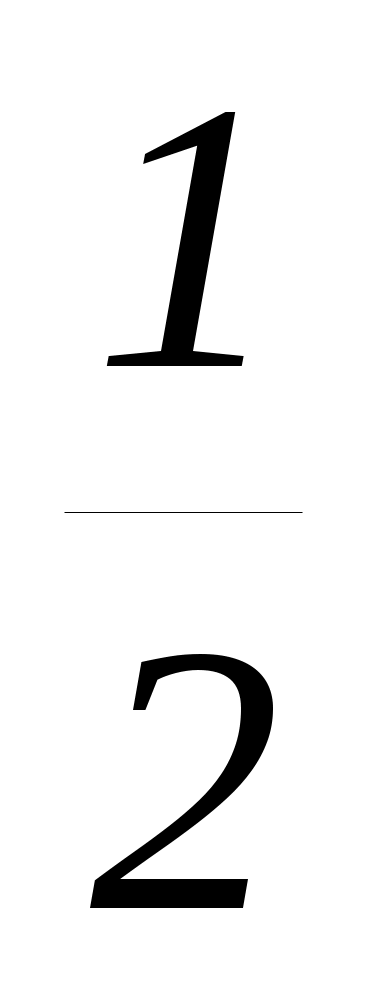 (3m + 1) 1, m
(3m + 1) 1, m
4.
f(1) 0; 1 + (3m + 1) + (2m2 + 4m 6) 0;
Ответ: а) m ; б) m 4.
; б) m 4.
Замечание: Если выражения для корней уравнения не содержат радикалов, то удобно решать примеры и без применения теорем. Так как корни х1 = m + 3, x2 = 2m 2, то в случае
а
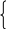 ) m + 3 1; m
) m + 3 1; m  ; б) m + 3 1; m 4.
; б) m + 3 1; m 4.
2m 2 1; 2m 2 1;
Ответ: (1;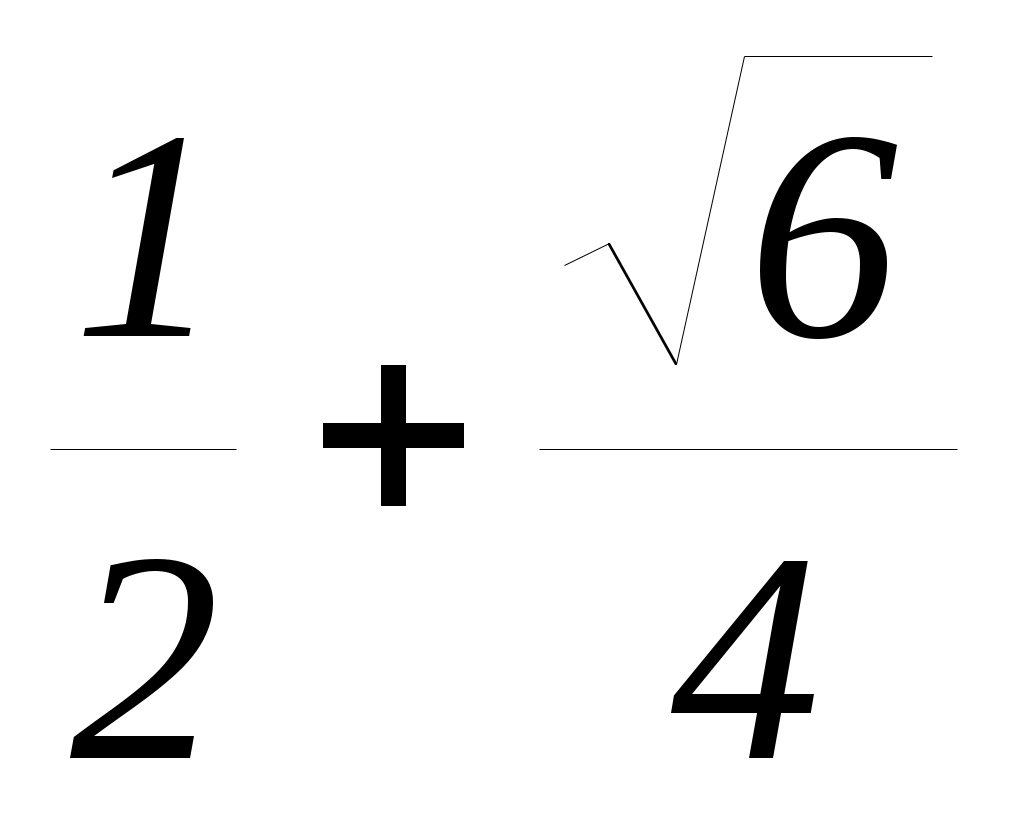 ].
].
Ответ: (1; + ).
Ответ: (3; + ).
У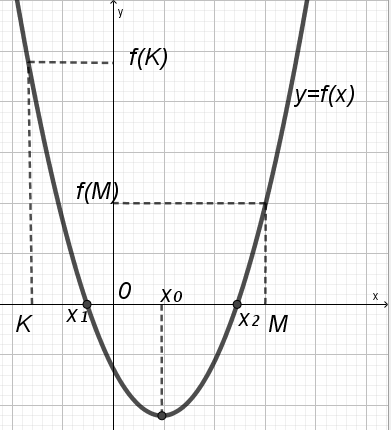 тверждение 5. Для того, чтобы оба корня квадратного трехчлена лежали в интервале (K; M), т. е. Kx1x2M, необходимо и достаточно выполнение условий:
тверждение 5. Для того, чтобы оба корня квадратного трехчлена лежали в интервале (K; M), т. е. Kx1x2M, необходимо и достаточно выполнение условий:
D 0;
0;
Kx0M;
А f(K) 0,
А f(M)
0.
Р
 ешение: D 0, 1 4m 0, m
ешение: D 0, 1 4m 0, m 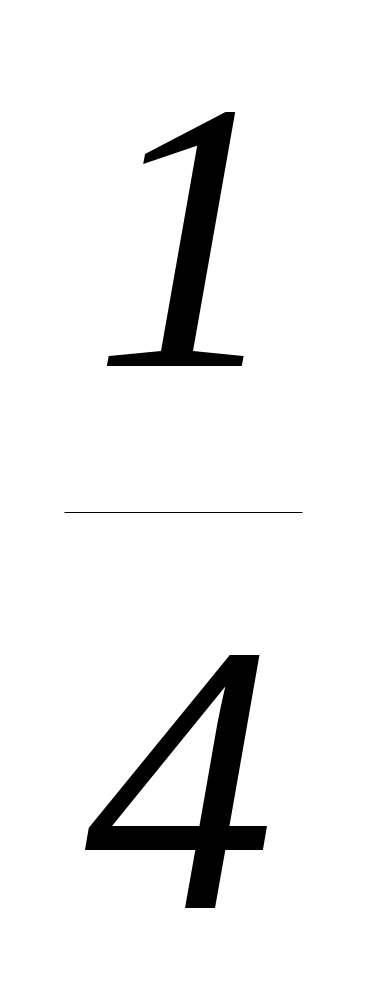 ,
,
1 x0 1, 1 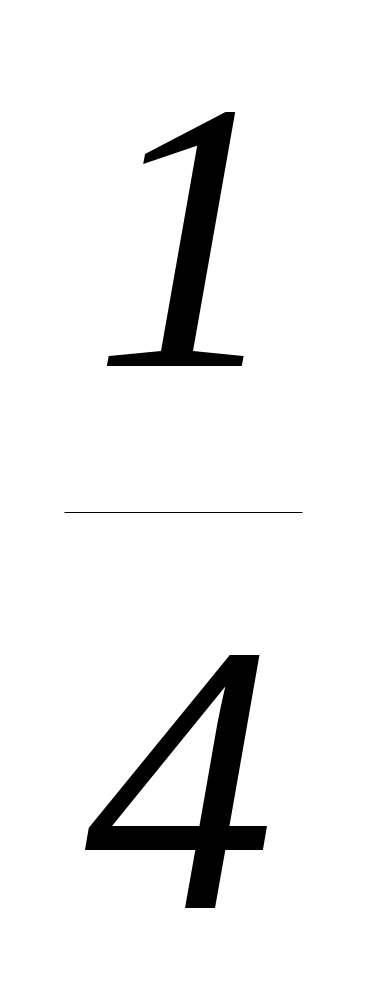 1, m 6, 2 m
1, m 6, 2 m 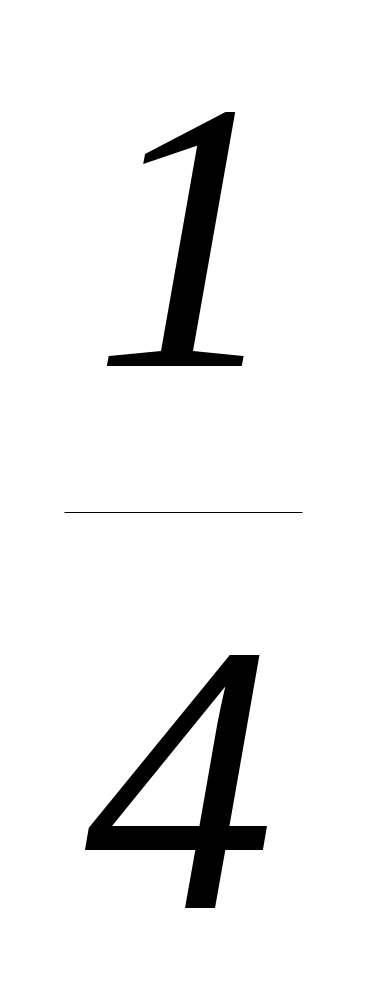 .
.
4 f(1) 0, 4 + 2 + m 0, m 2;
4 f(1) 0; 4 2 + m 0;
Ответ: (2;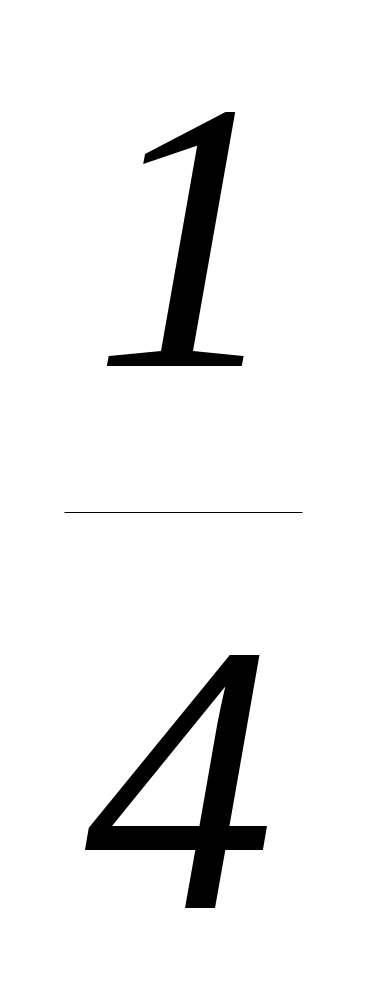 ].
].
Условие задачи можно сформулировать следующим образом: при каких m
4 х1 х2 4?
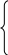
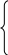
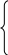 Решение: D 0, m2 (m2 2m + 5) 0, m
Решение: D 0, m2 (m2 2m + 5) 0, m 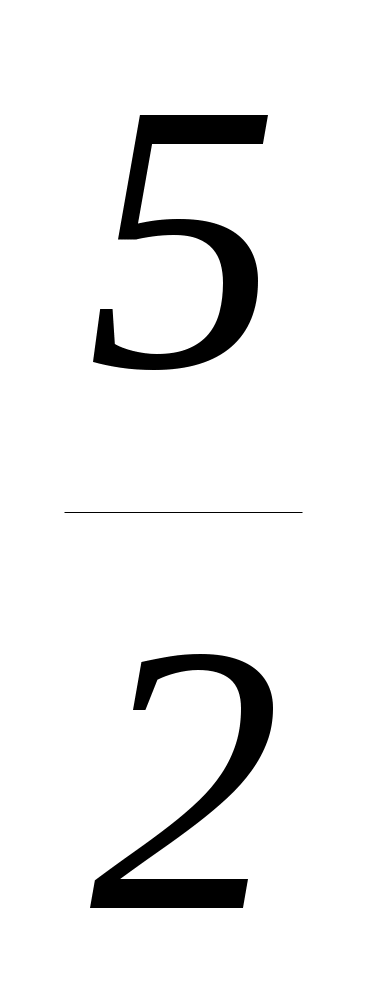 ,
,
4 x0 4, 4 m 4, 4 m 4, f( 4) 0, 16 + 8m + m2 2m + 5 0, m2 + 6m + 21 0,
f(4) 0; 16 8m + m2 2m + 5 0; m2 10m + 21 0.
Ответ: [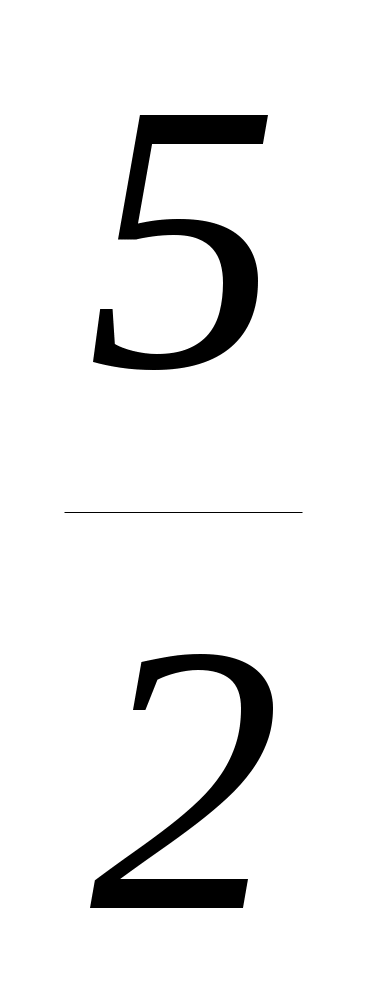 ; 3].
; 3].
Утверждение 6. Для того, чтобы больший корень квадратного трехчлена принадлежал интервалу (N; M
), а меньший не принадлежал, необходимо и достаточно выполнение условий:
А f(N) 0,
f(N) 0,
А f(M) 0.
У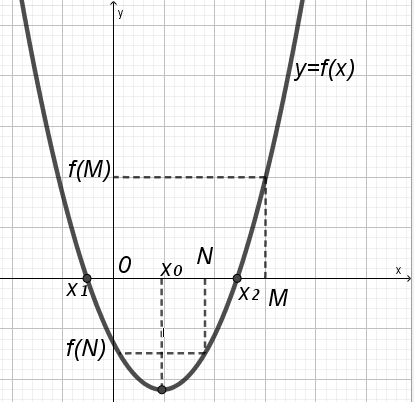 тверждение 7. Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (N; M), а больший не принадлежал, необходимо и достаточно выполнение условий:
тверждение 7. Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (N; M), а больший не принадлежал, необходимо и достаточно выполнение условий:
А f(N) 0,
f(N) 0,
А f(M) 0.
У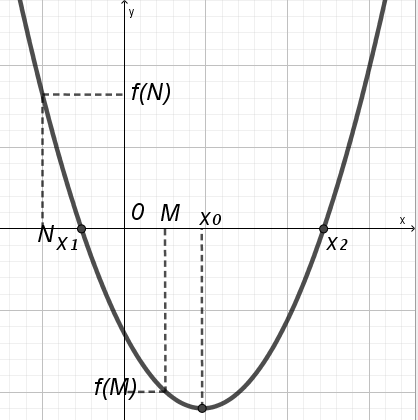 тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства
тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства
f(N)f(M) 0.
При решении задач следует отдельно рассматривать случаи D = 0 и A = 0.
Решение: 1) f(2)f(5) 0; (10 2p) (31 5p) 0; 5 p .
.
2) Если D = 0, то уравнение имеет один корень.
D = p2 24; p2 24 = 0; p = 2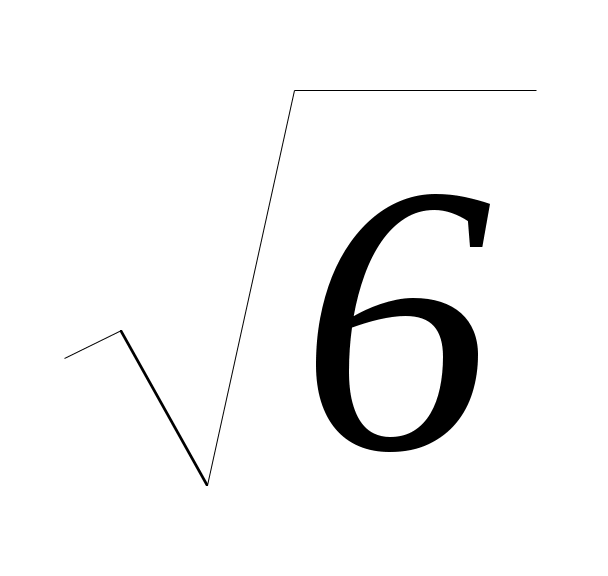 ;
;
а) при p = 2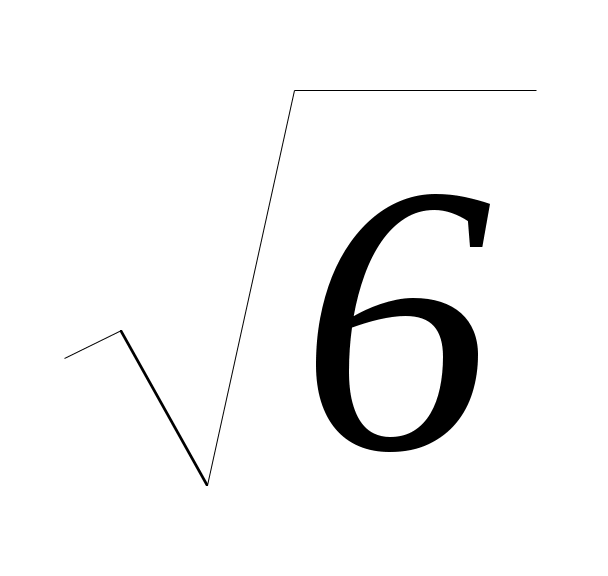 , х =
, х = 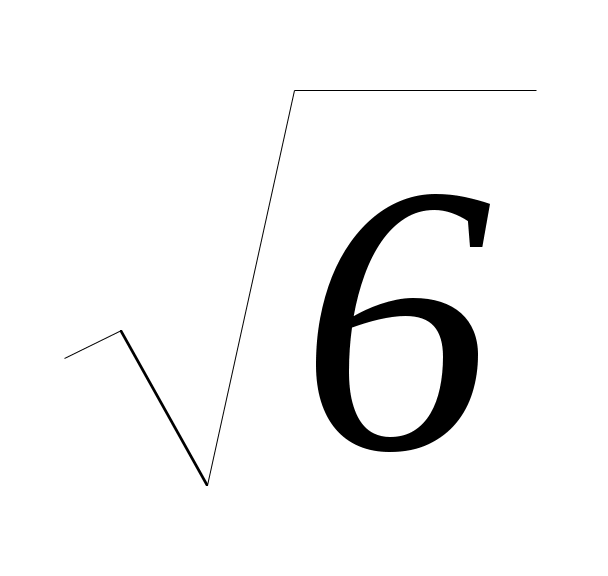 ;
; 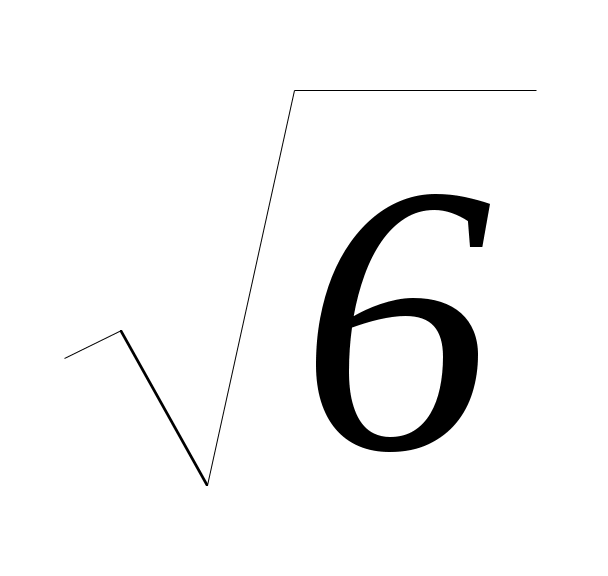 (2; 5);
(2; 5);
б) при p = 2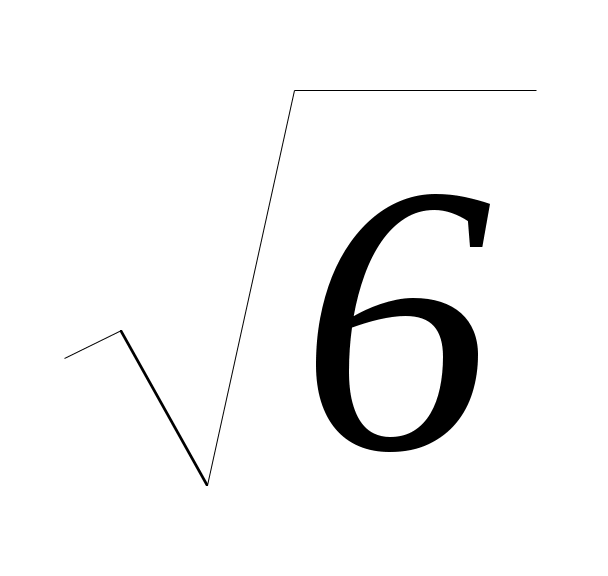 , х =
, х = 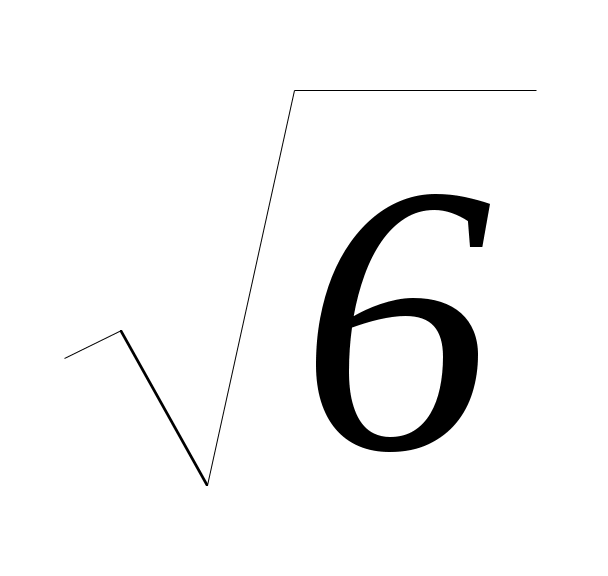 ;
; 
(m 1) f(4) 0; (m 1)(11m 32) 0; 1 m
Ответ: (1;
-
Найти все значения а, при которых неравенство x2 2(а 3)x + а2 6а 0 будет выполнено для любого х, принадлежащего интервалу (0; 2).
Решение: Интервал (0; 2) должен содержаться во множестве решений данного неравенства, следовательно, должно выполняться соотношение
х1 0 2 х2
 f(0) 0, a2 6a 0, 0 a 6, 2 a 6.
f(0) 0, a2 6a 0, 0 a 6, 2 a 6.f(2) 0; 4 + 4(a 3) + a2 6a 0; 2 a 8;
Ответ: [2; 6].
У
 тверждение 3. Для того, чтобы оба корня квадратного трехчлена были меньше числа M (х1х2M), необходимо и достаточно выполнение условий:
тверждение 3. Для того, чтобы оба корня квадратного трехчлена были меньше числа M (х1х2M), необходимо и достаточно выполнение условий:D
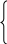 0;
0;x0M;
А f(M) 0.
Доказательство.
(x1M) 0; (x2M) 0;
(x1M)(x2M) 0;
M2 (x1 + x2)M + x1 x2 0;
M2 +
0 xa2;
a(aM2 + BM + C) 0;
af(M) 0.
У
 тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (Kх1х2), необходимо и достаточно выполнение условий:
тверждение 4. Для того, чтобы оба корня уравнения были больше числа K (Kх1х2), необходимо и достаточно выполнение условий:D
 0;
0;x0K;
А f(K) 0.
-
При каких mвсе корни уравнения x2 (3m + 1)x + (2m2 + 4m 6) = 0
а) больше 1; б) меньше 1?
Р
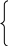
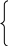
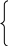 ешение: а) D 0, (3m + 1)2 4(2m2 + 4m 6) 0, (m 5)2 0,
ешение: а) D 0, (3m + 1)2 4(2m2 + 4m 6) 0, (m 5)2 0,x0 1,
f(1) 0; 1 (3m + 1) + (2m2 + 4m 6) 0; (2m 3)(m + 2) 0;
 mлюбое число,
mлюбое число,m
 m2,
m2,m
б
 ) D 0, mлюбое число,
) D 0, mлюбое число, x01,
4.
f(1) 0; 1 + (3m + 1) + (2m2 + 4m 6) 0;
Ответ: а) m
Замечание: Если выражения для корней уравнения не содержат радикалов, то удобно решать примеры и без применения теорем. Так как корни х1 = m + 3, x2 = 2m 2, то в случае
а
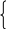 ) m + 3 1; m
) m + 3 1; m 2m 2 1; 2m 2 1;
-
При каких а корни уравнения аx2 (2а + 1)x + 3а 1 = 0 больше 1?
Ответ: (1;
-
При каких р корни уравнения x2 + 4рх + (1 2р + 4р2) = 0 меньше 1?
Ответ: (1; + ).
-
При каких bкорни уравнения x2 2xb = 0 меньше b?
Ответ: (3; + ).
У
 тверждение 5. Для того, чтобы оба корня квадратного трехчлена лежали в интервале (K; M), т. е. Kx1x2M, необходимо и достаточно выполнение условий:
тверждение 5. Для того, чтобы оба корня квадратного трехчлена лежали в интервале (K; M), т. е. Kx1x2M, необходимо и достаточно выполнение условий: D
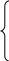 0;
0;Kx0M;
А f(K) 0,
А f(M)
0.
-
Для каких значений mуравнение 4x2 2x + m = 0 имеет корни, заключенные между 1 и 1?
Р
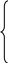
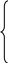
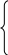 ешение: D 0, 1 4m 0, m
ешение: D 0, 1 4m 0, m 1 x0 1, 1
4 f(1) 0, 4 + 2 + m 0, m 2;
4 f(1) 0; 4 2 + m 0;
Ответ: (2;
-
При каких mкорни уравнения x2 2mx + m2 2m + 5 = 0 по модулю не превосходят 4?
Условие задачи можно сформулировать следующим образом: при каких m
4 х1 х2 4?
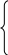
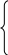
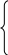 Решение: D 0, m2 (m2 2m + 5) 0, m
Решение: D 0, m2 (m2 2m + 5) 0, m 4 x0 4, 4 m 4, 4 m 4, f( 4) 0, 16 + 8m + m2 2m + 5 0, m2 + 6m + 21 0,
f(4) 0; 16 8m + m2 2m + 5 0; m2 10m + 21 0.
Ответ: [
Утверждение 6. Для того, чтобы больший корень квадратного трехчлена принадлежал интервалу (N; M
), а меньший не принадлежал, необходимо и достаточно выполнение условий:
А
 f(N) 0,
f(N) 0,А f(M) 0.
У
 тверждение 7. Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (N; M), а больший не принадлежал, необходимо и достаточно выполнение условий:
тверждение 7. Для того, чтобы меньший корень квадратного трехчлена принадлежал интервалу (N; M), а больший не принадлежал, необходимо и достаточно выполнение условий: А
 f(N) 0,
f(N) 0,А f(M) 0.
У
 тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства
тверждение 8. Для того, чтобы только один корень квадратного трехчлена принадлежал интервалу (N; M), необходимо и достаточно выполнение неравенства f(N)f(M) 0.
При решении задач следует отдельно рассматривать случаи D = 0 и A = 0.
-
При каких р только один корень уравнения x2 рx + 6 = 0 удовлетворяет условию 2 х 5?
Решение: 1) f(2)f(5) 0; (10 2p) (31 5p) 0; 5 p
2) Если D = 0, то уравнение имеет один корень.
D = p2 24; p2 24 = 0; p = 2
а) при p = 2
б) при p = 2