ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 122
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
30 человек.
Так как меньшее число учащихся может быть в 7-м и 9-м классах, то должны выполняться неравенства 36 – 30 и 33 –
30 и 33 –  30. Отсюда получаем, что n 18 и n 9. Следовательно, n 9.
30. Отсюда получаем, что n 18 и n 9. Следовательно, n 9.
Из того, что числа 36 – , 36 +
, 36 +  и 33 –
и 33 –  должны быть натуральными, следует, что nкратно 3.
должны быть натуральными, следует, что nкратно 3.
Учитывая эти два условия (n 9 и nкратно 3), заключаем, что nравно 3, 6 или 9.
Поэтому окончательный ответ на вопрос задачи мы можем записать так: в 7-м классе было 36 – учащихся, в 8-м классе 36 +
учащихся, в 8-м классе 36 +  и в 9-м классе 33 –
и в 9-м классе 33 –  , где n = 3, n = 6, n = 9.
, где n = 3, n = 6, n = 9.
Иначе говоря, возможны три варианта: в 7-м, 8-м и 9-м классах могло быть соответственно 35, 38, 32; или 34, 40, 31; или 33, 42, 30 учащихся.
Задача очень объемная. Цель ее рассмотрения:
Поэтому целесообразно первую часть разобрать в форме диалога с учащимися, а далее конструктивно перейти к ответу, акцентировать внимание на возможных значениях n. Непосредственно закончить решение задачи предлагается самостоятельно по желанию, с последующим выставлением оценки в журнал, либо разобрать на факультативном занятии.
Во вводной беседе следует заметить, что изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Наиболее трудной и важной частью решения таких задач является исследование процесса в зависимости от параметров.
Формированию некоторых навыков решения таких задач и посвящена данная тема.
Итак, решение линейного уравнения
ax = b в общем виде, исследование количества его корней в зависимости от значений параметра относится к задачам с параметром.
Решим ряд устных упражнений типа:
Какое уравнение получится при а) a = 10; б) a = 2;
в) a = ¼; г) a = 0.
а) относительно x;
б) относительно a.
Найдите множество корней этого уравнения в случае, если a = 4, a 4.
После этого восстановим схему решения линейного уравнения ax = b (x – переменная, a, b – некоторые числа). Для этого можно пригласить к доске сильного ученика.
 ax = b
ax = b

a 0, b – любое a = 0
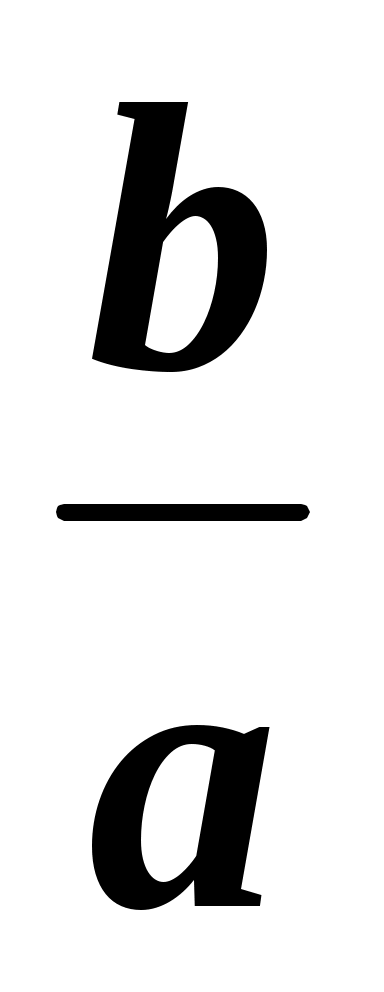
x = b = 0b 0
0 x = 0 0 x = b
x – любое числокорней нет
Однако, учитывая, что решение задачи обычно записывается не блок-схемой, предпочтительно знакомить учащихся со словесным алгоритмом решения. Его они и записывают в тетрадь вслед за учителем.
Алгоритм решения линейных уравнений с параметром.
Ax = B (x – неизвестное,
A, B – выражения, зависящие только от параметров)
Уравнение имеет один корень, причем x 0, если a 0 и b 0 или a 0 и b 0;
x = 0, если b = 0;
x 0, если a 0 и b 0 или a 0 и b 0.
0 x = 0, x – любое число.
Уравнение имеет бесконечно много корней.
б) Если A = 0, B 0
0 x = B, корней нет.
Уравнение корней не имеет.
Сначала прорешиваем ключевые уравнения, акцентируя внимание на правильную запись ответа.
Решение: а) Если a 0, то x =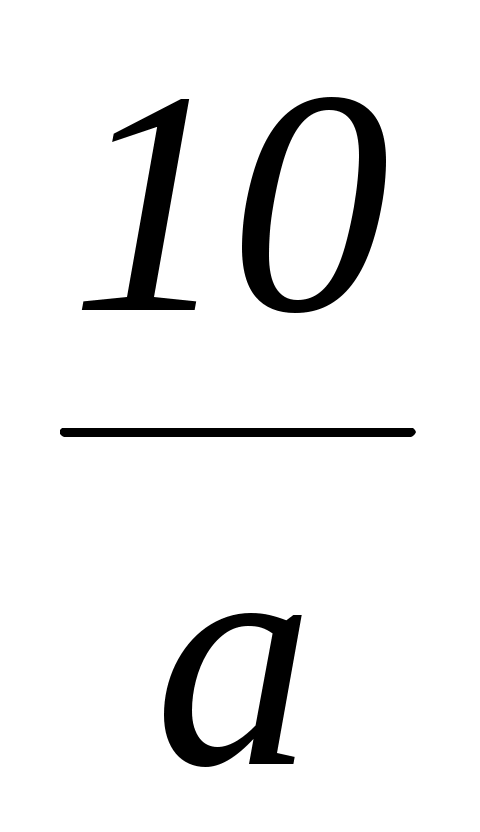 ;
;
б) Если a = 0, то 0 x =10, корней нет.
Ответ: при a 0 x =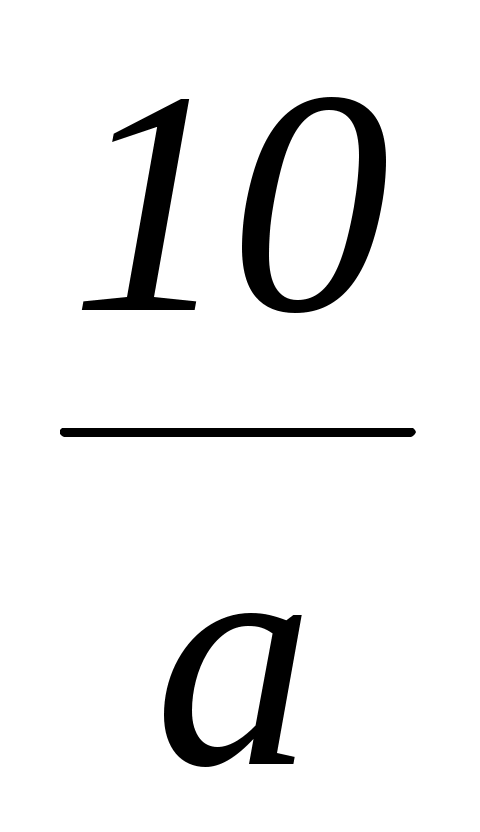 ;
;
при a = 0 корней нет.
Решение: а) Если a = 0, то 0 x = 0, x – любое число;
б) Если a 0, то 0 x = a, корней нет.
Ответ: при a = 0 x – любое число;
при a 0 корней нет.
Обращаем внимание, что значение коэффициента известно, буквой a обозначен свободный член. При решении данного уравнения работает второй шаг алгоритма.
Решение: 1. Если 2m (m – 2) 0, то m 0, m 2;
x =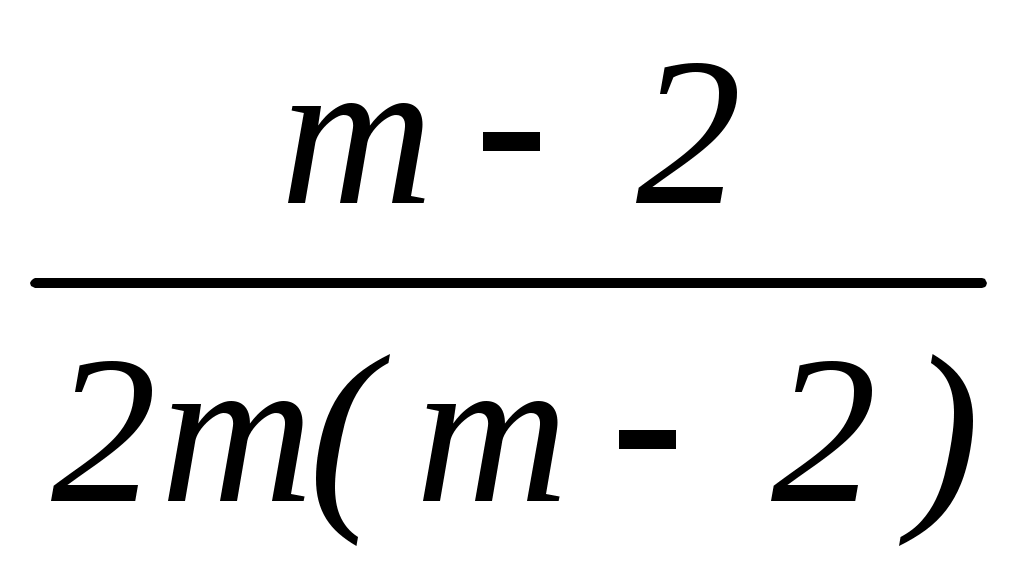 ; x =
; x =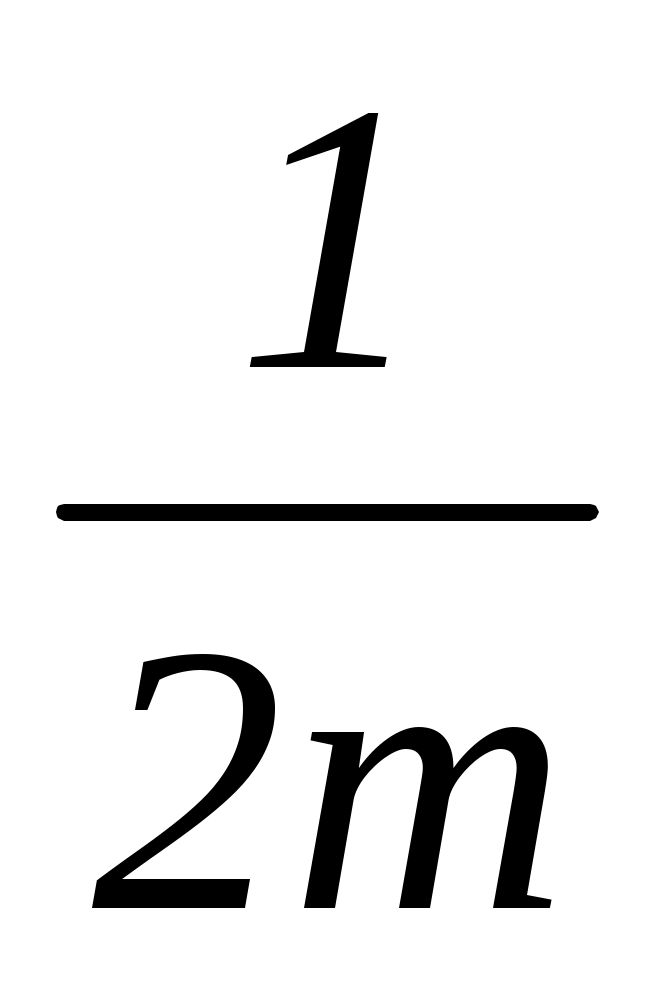 .
.
2. а) Если m = 0, то
(на первых порах записываем подробно, чтобы ученики видели источник появления уравнения)
2 0 (0 – 2) x = 0 – 2,
0 x = – 2,
корней нет.
б) Если m = 2, то
2 2 (2 – 2) x = 2 – 2,
0 x = 0,
x – любое число.
Ответ: при m 0, m 2 x =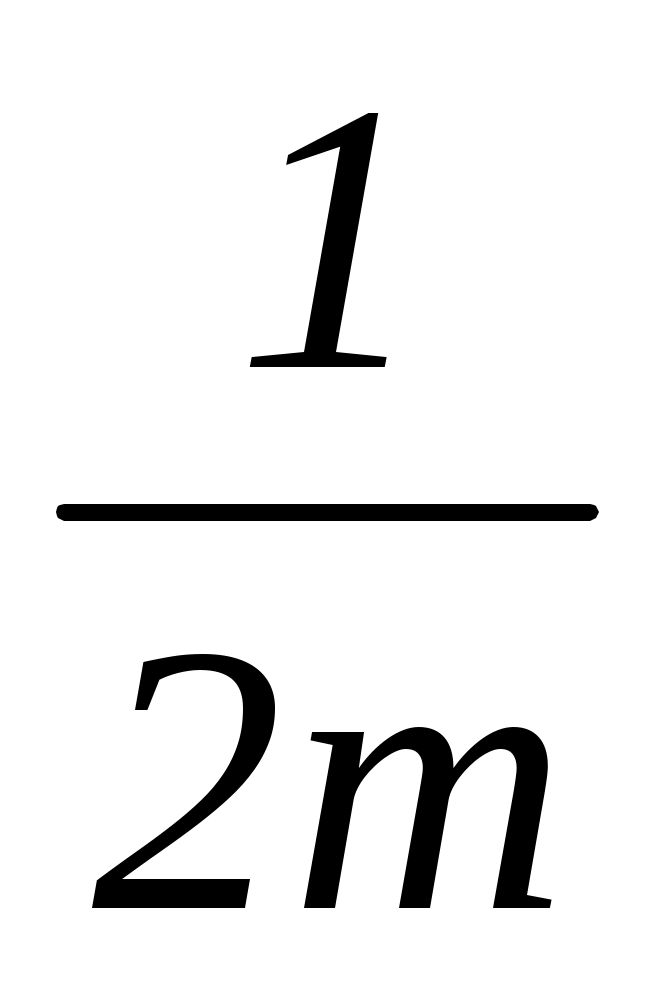 ;
;
при m = 0 корней нет;
при m = 2 x – любое число.
Решение: Преобразуем уравнение к виду ax = b.
ax + 2x = 4a – 3,
(a + 2) x = 4a – 3.
1. Если a + 2 0, то a –2, x =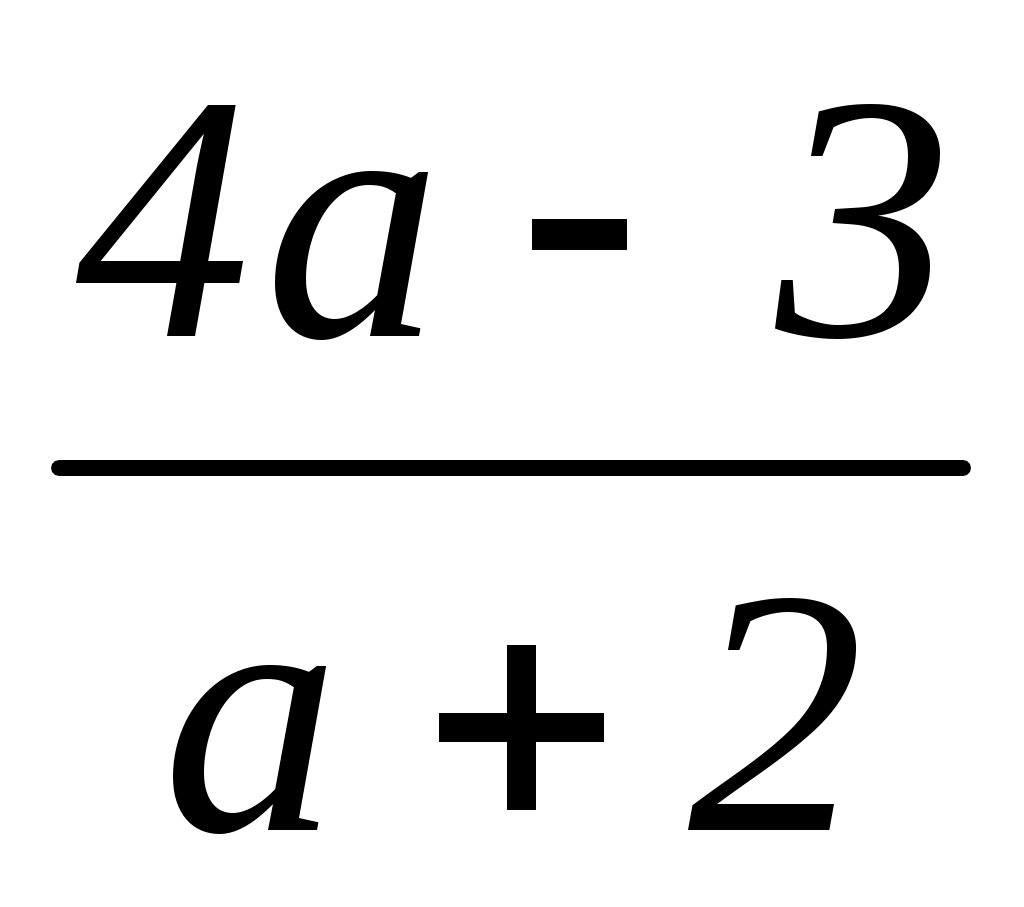 ;
;
2. Если a = –2, то (–2 + 2) x = 4 (–2) – 3,
0 x = –11,
корней нет.
Ответ: при a –2 x =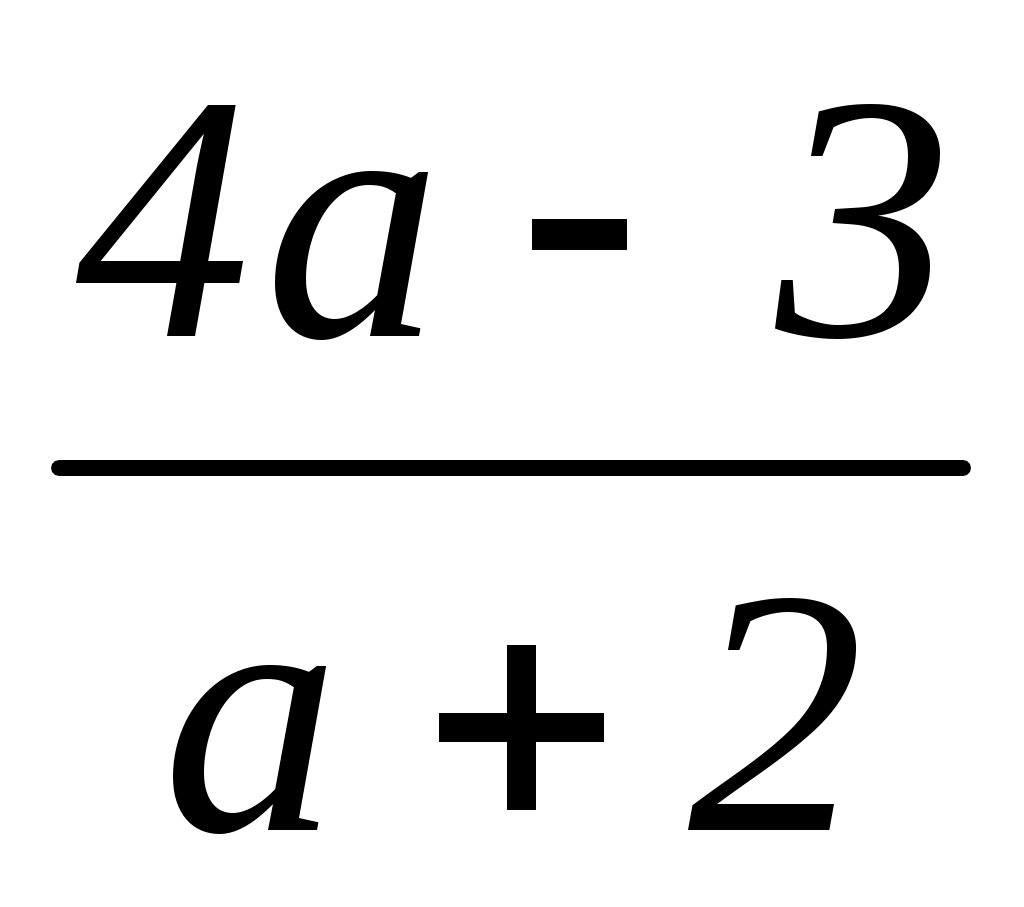 ;
;
при a = –2 корней нет.
а) больший нуля; б) меньший нуля; в) равный нулю?
Решение: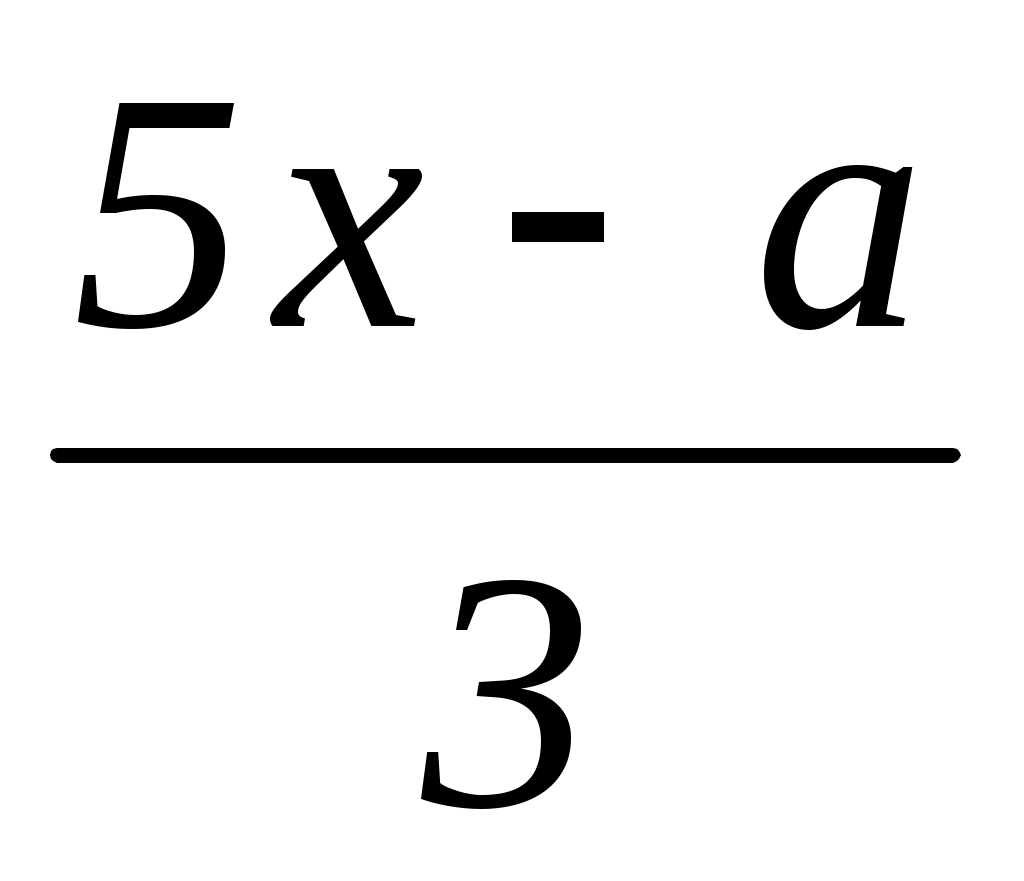 =
= 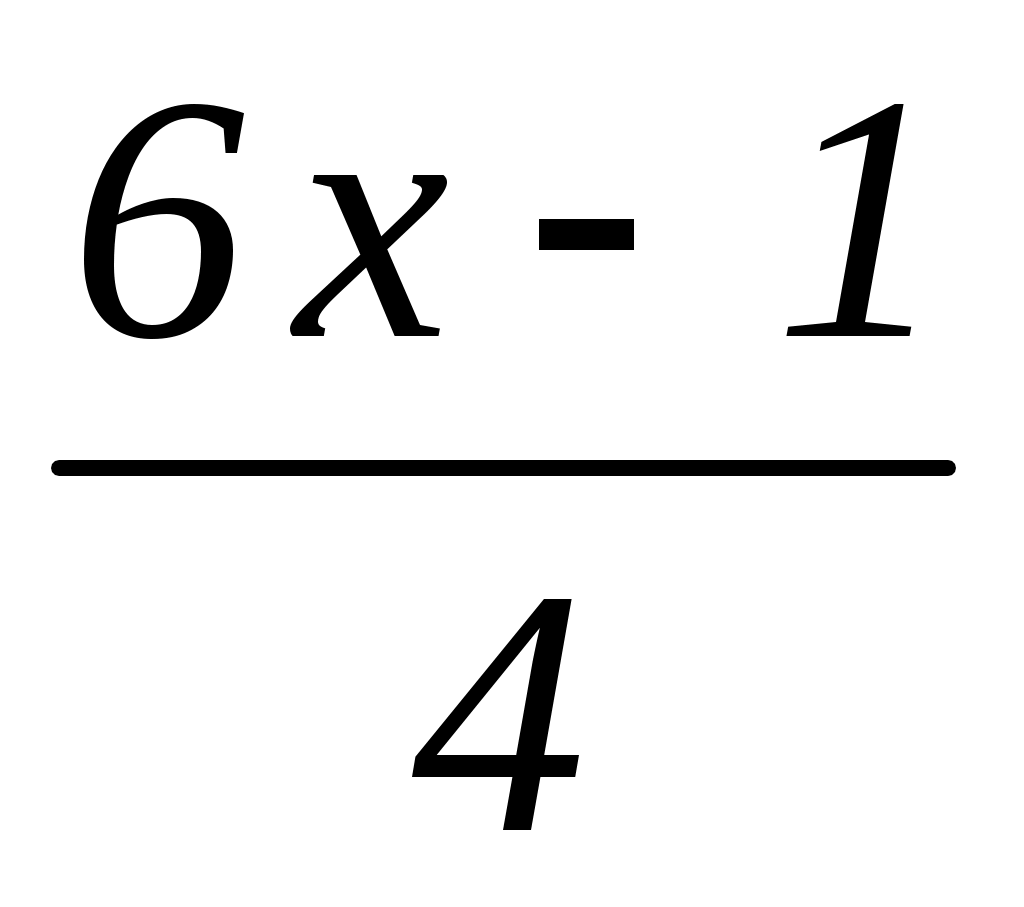
Умножим обе части уравнения на 12:
20x – 4a = 18x – 3;
20x – 18x = 4a – 3;
2x = 4a – 3;
x =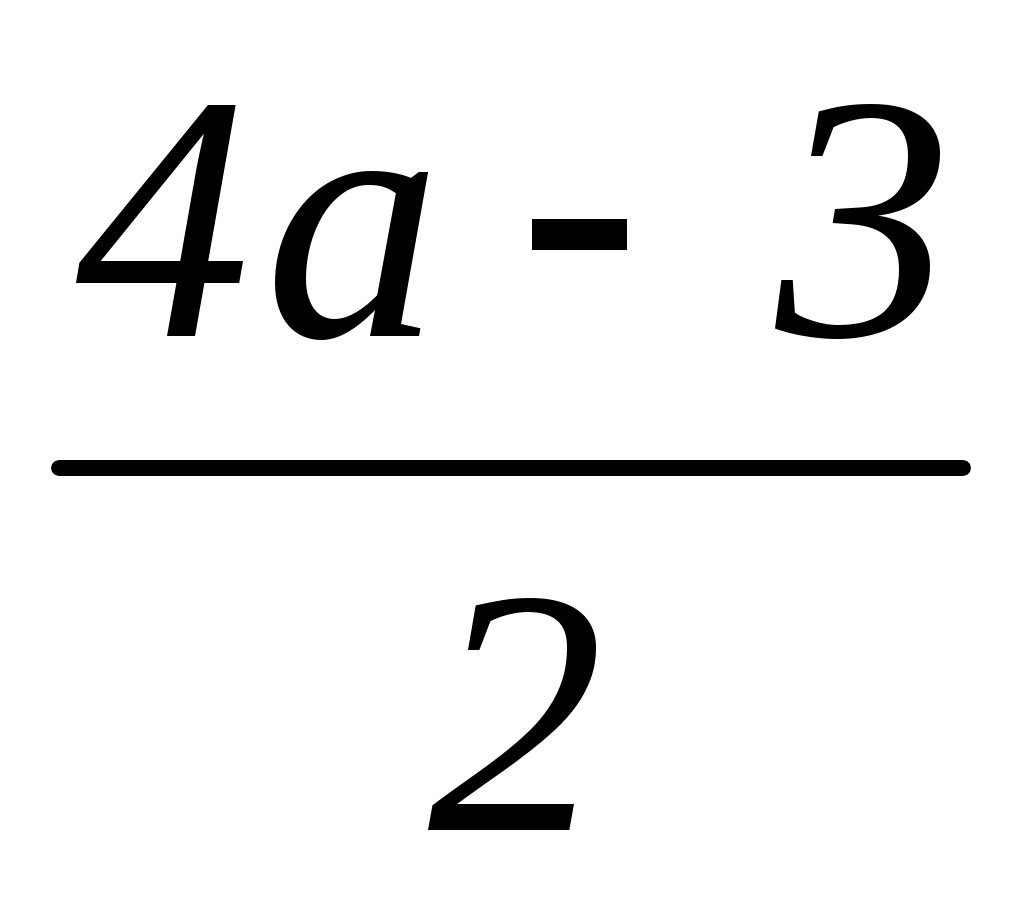 ;
;
x = 2a – 1,5.
а) x 0, если 2a – 1,5 0, 2a 1,5, a 0,75;
б) x 0, если 2a – 1,5 0, 2a 1,5, a 0,75;
в) x = 0, если 2a – 1,5= 0, 2a = 1,5, a = 0,75.
Ответ: при a 0,75 x 0;
при a 0,75 x 0;
при a = 0,75 x = 0.
Далее учащиеся решают блок задач на отработку задач типа 15. Такие задачи составляются весьма легко.
Разные задачи
Ответ: (a2 + 1) x = a или ax = a
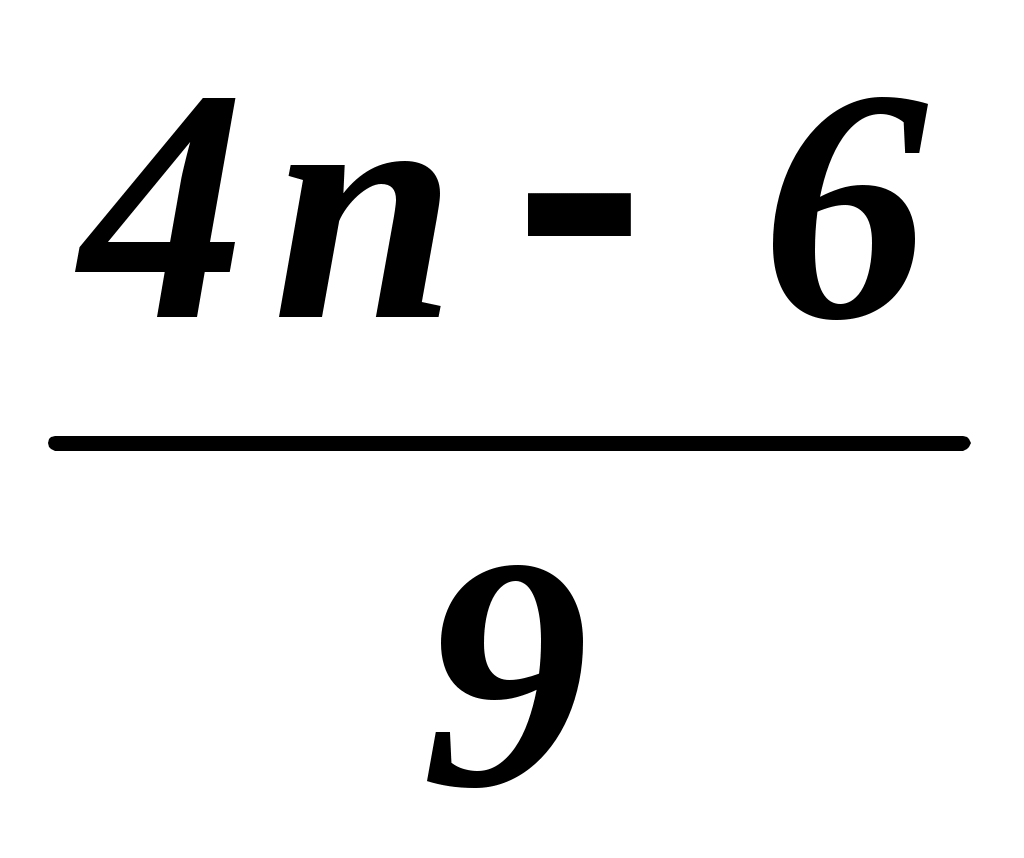 –
– 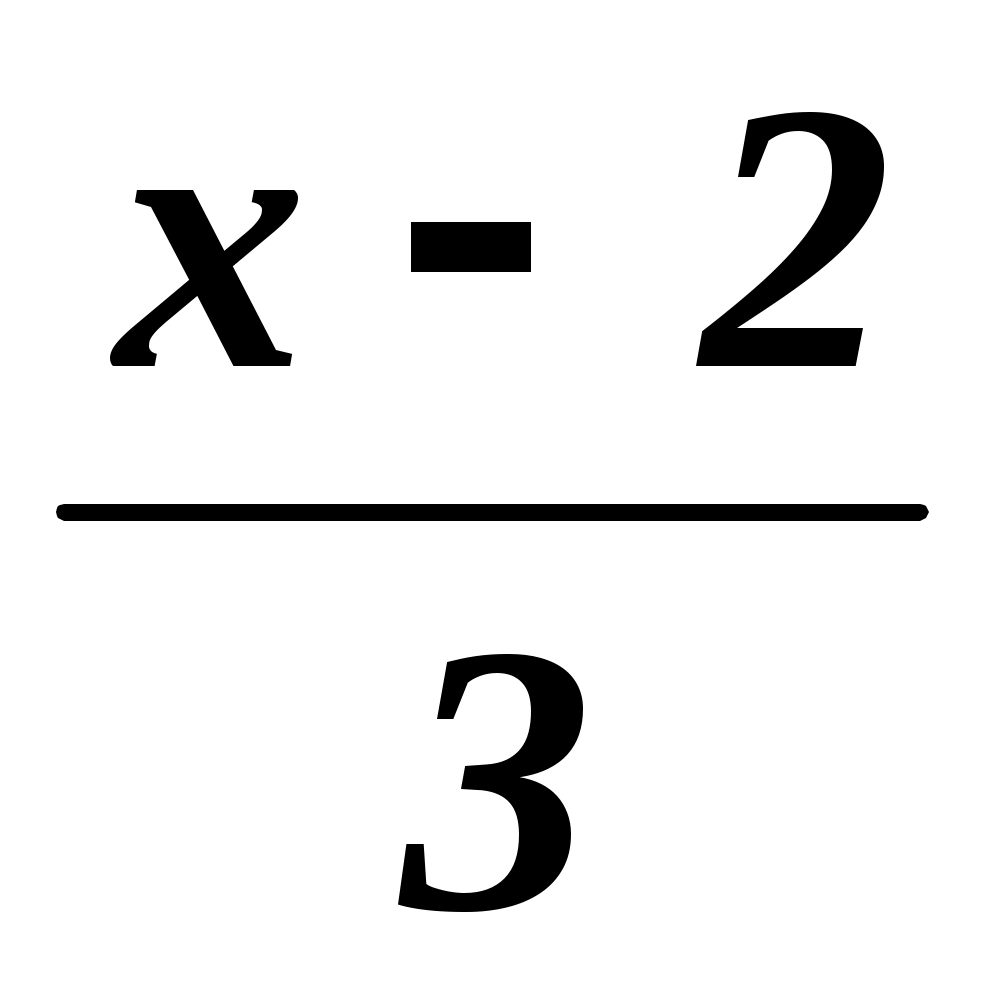 = 1 ?
= 1 ?
Решение: Умножим обе части уравнения на 9:
4n – 6 – 3 (x – 2) = 9;
4n – 6 – 3x + 6 = 9;
–3x = 9 – 4n;
x =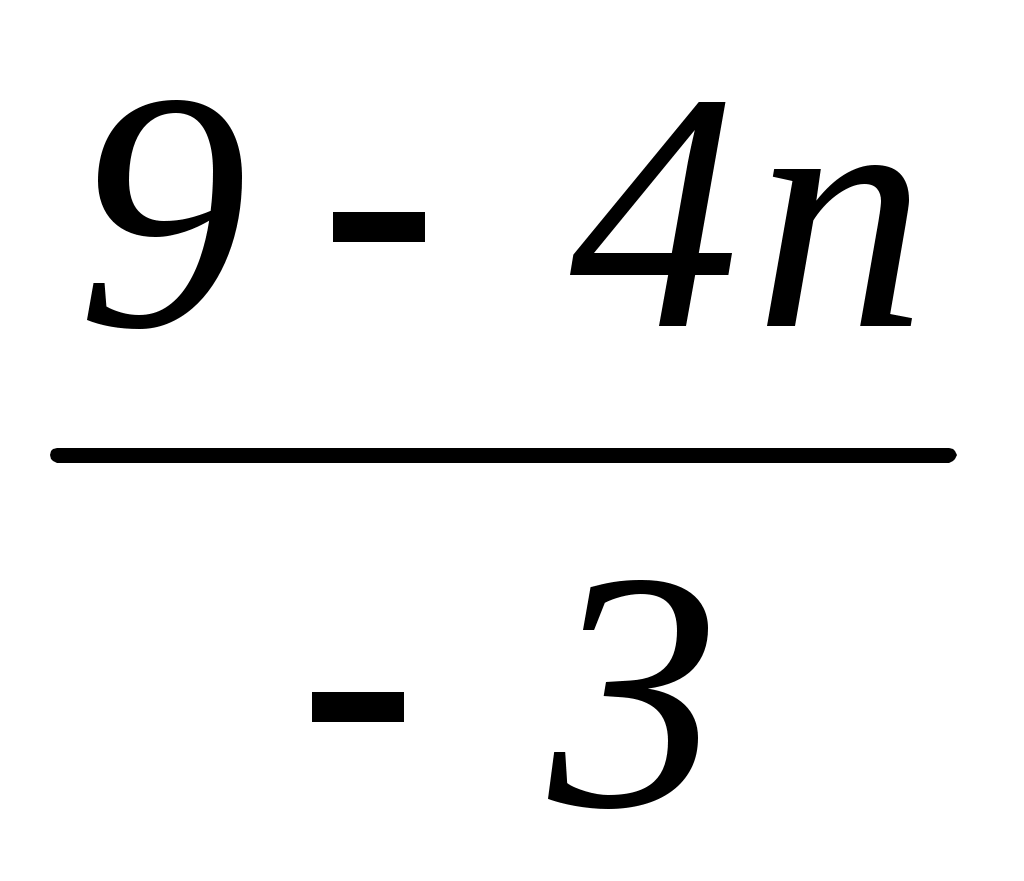 ;
;
x =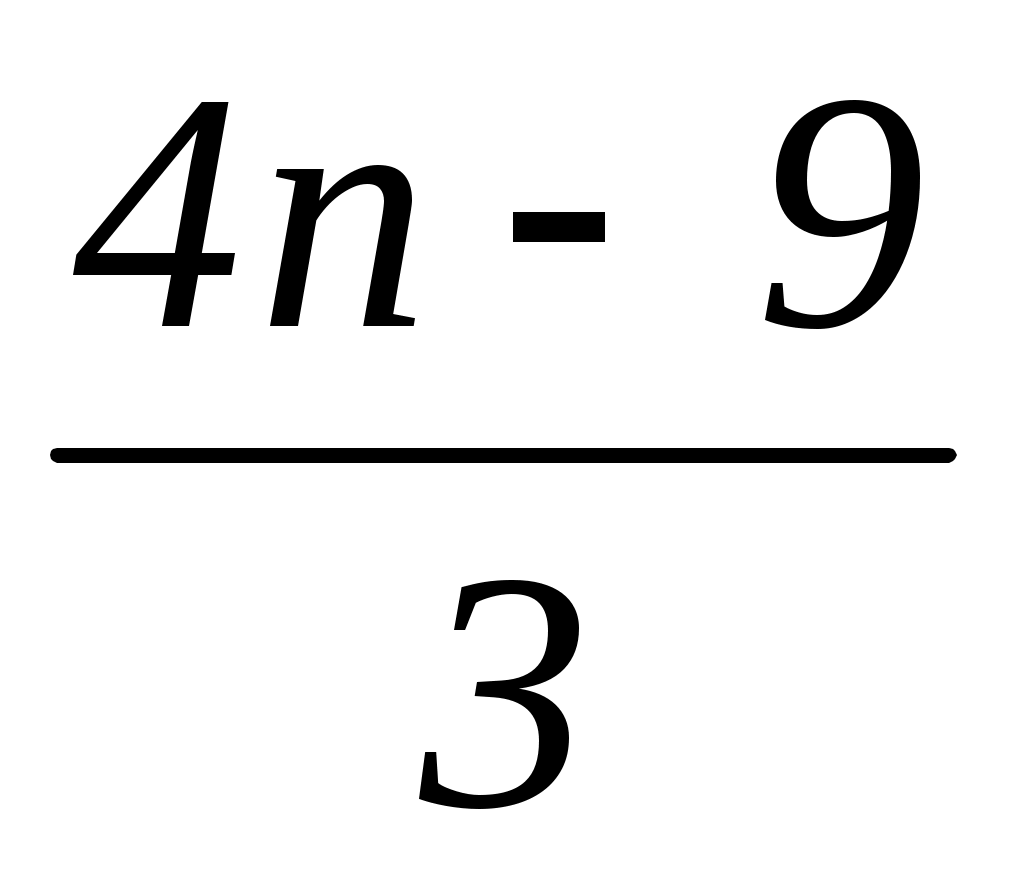 .
.
Уравнение имеет целые корни, если 4n – 9 кратно числу 3, следовательно, 4n кратно числу 3, отсюда n = 3k, где k – натуральное число.
Ответ: n = 3k, k N.
Решение: Решим это уравнение относительно x, т.е. букву y будем считать параметром. Имеем:
x – xy = 7 – 5y;
x (1 – y) = 7 – 5y;
x =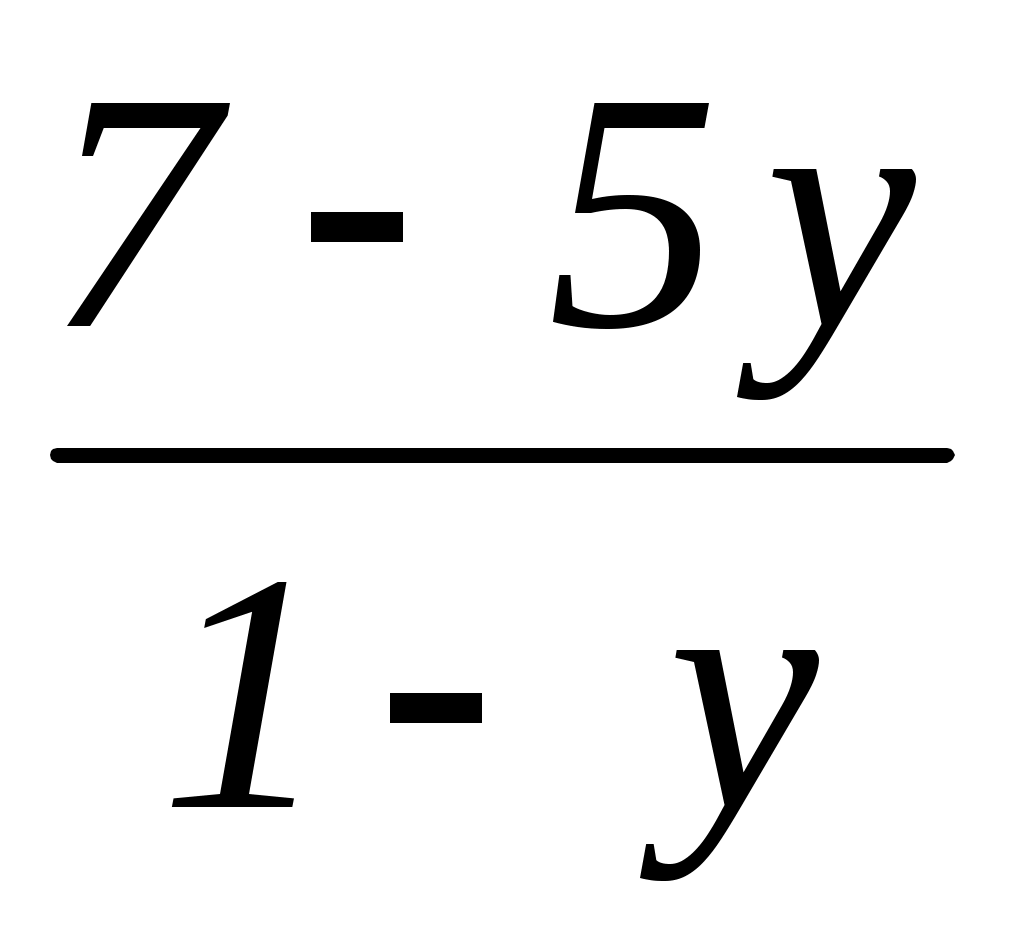 ;
;
Выделим из дроби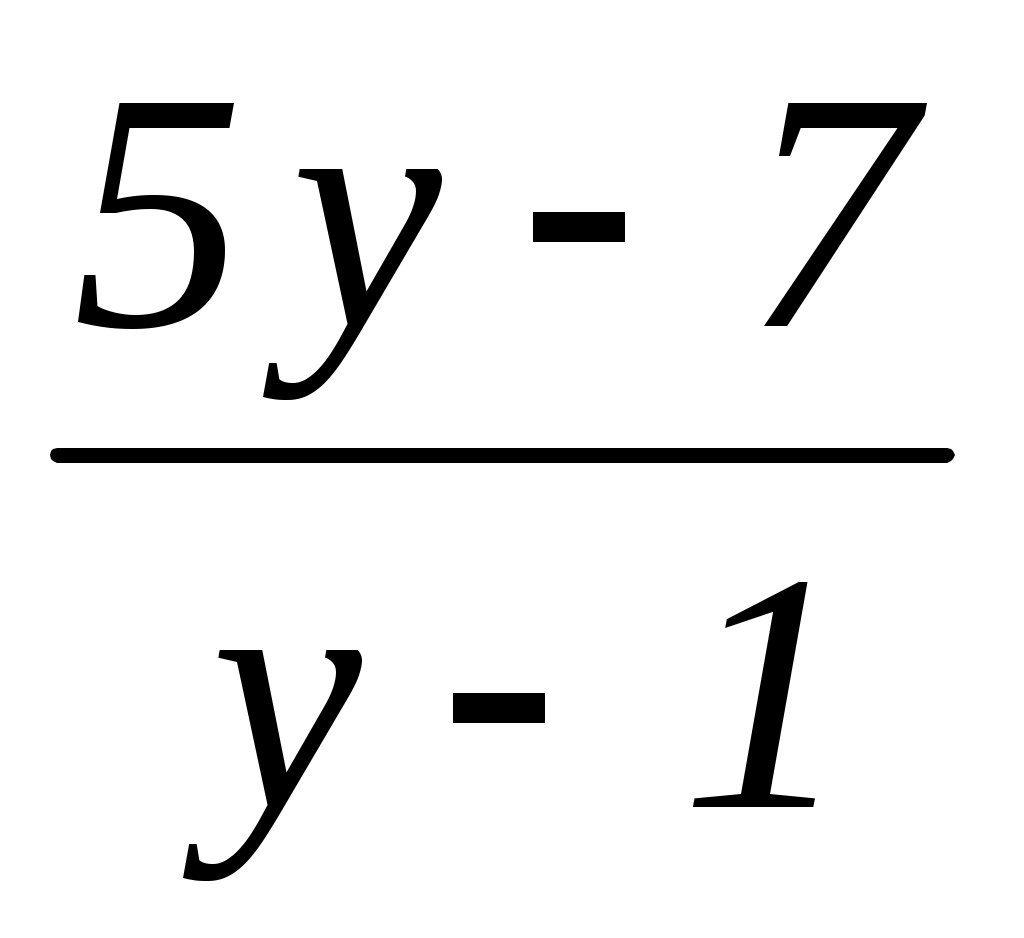 целую часть:
целую часть:
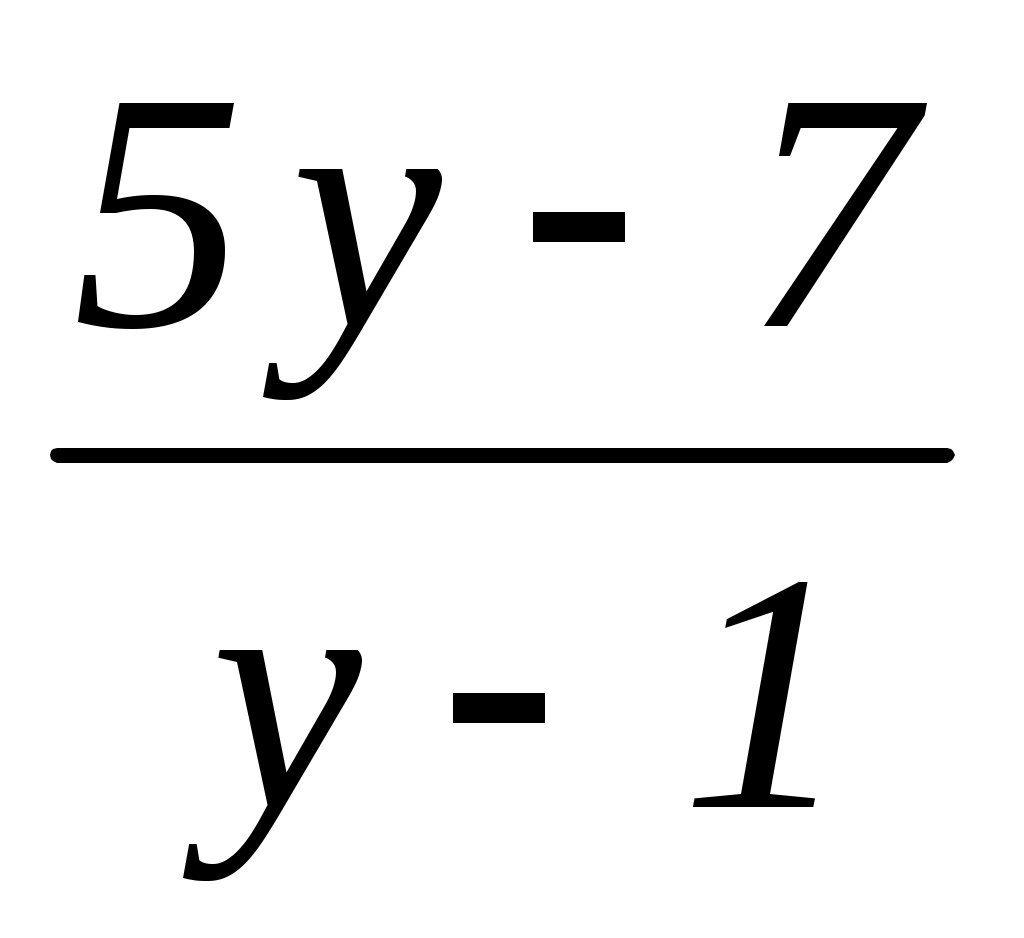 =
= 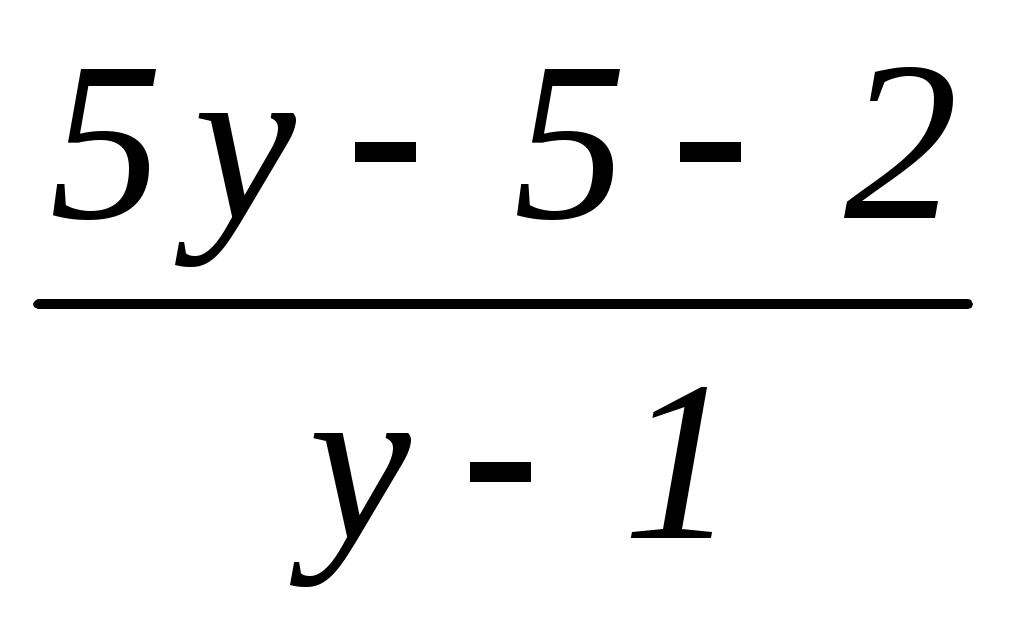 =
= 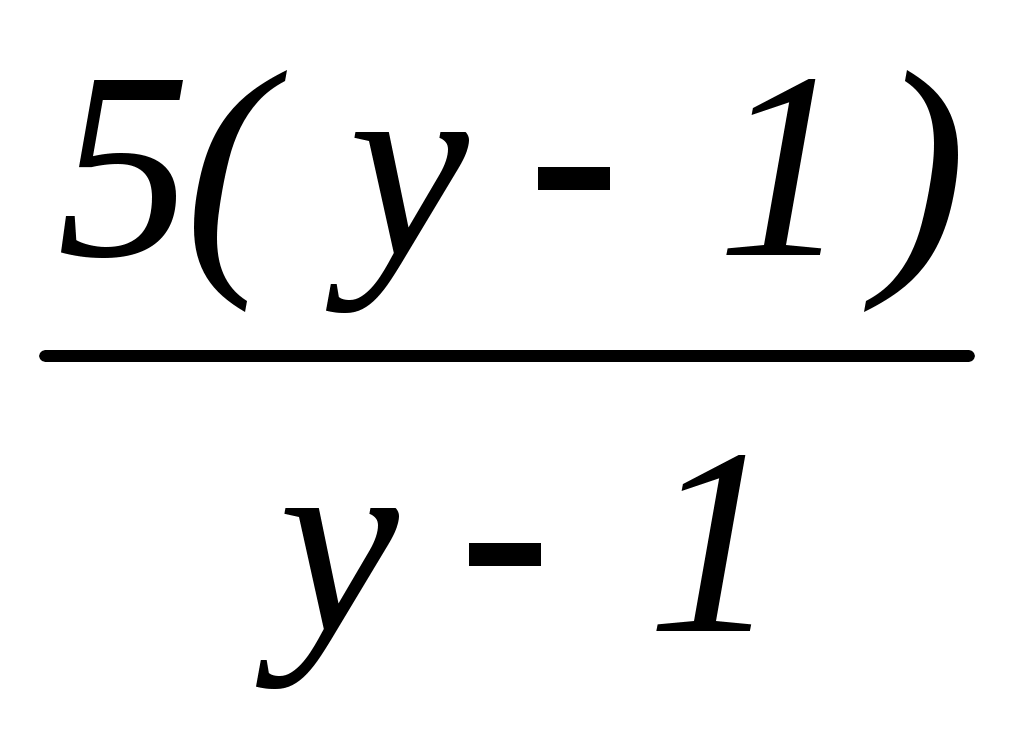 –
– 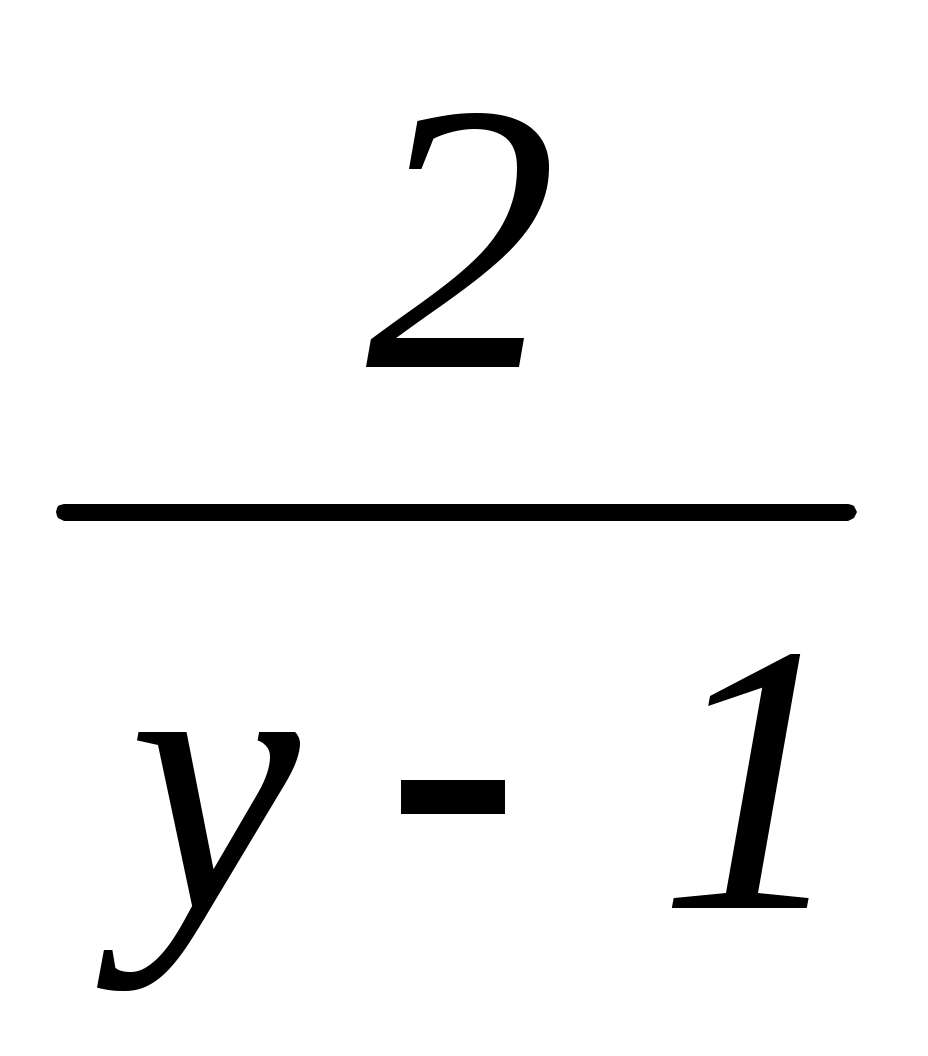 = 5 –
= 5 – 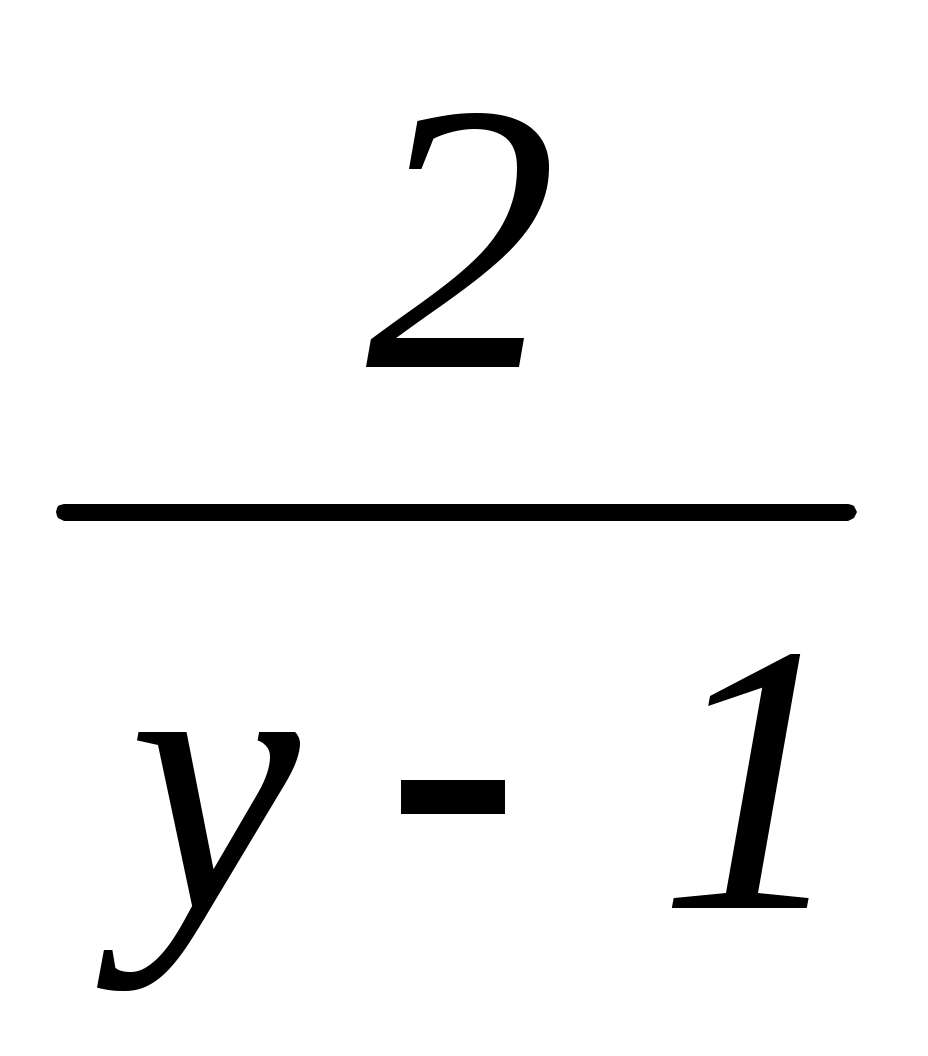 .
.
Итак, x = 5 – . Дробь
. Дробь  обращается в целое число лишь при тех значениях y, при которых y – 1 является делителем числа 2, т.е. при y, равном –1, 0, 2, 3.
обращается в целое число лишь при тех значениях y, при которых y – 1 является делителем числа 2, т.е. при y, равном –1, 0, 2, 3.
Вычислим соответствующие значения x:
Если y = –1, то x = 5 –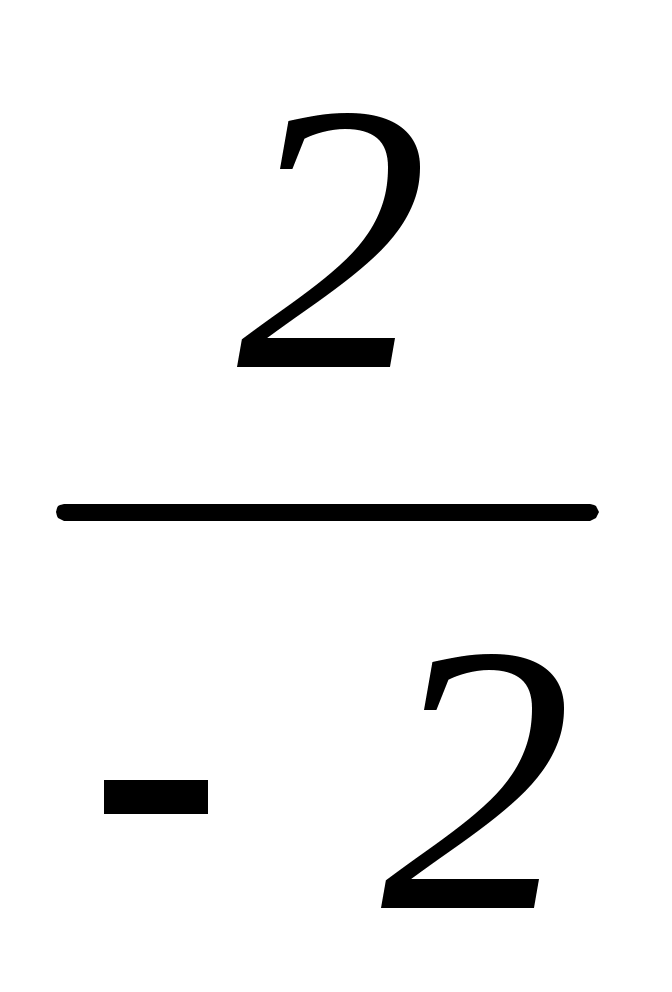 = 6;
= 6;
Если y = 0, то x = 5 – = 7;
= 7;
Если y = 2, то x = 5 –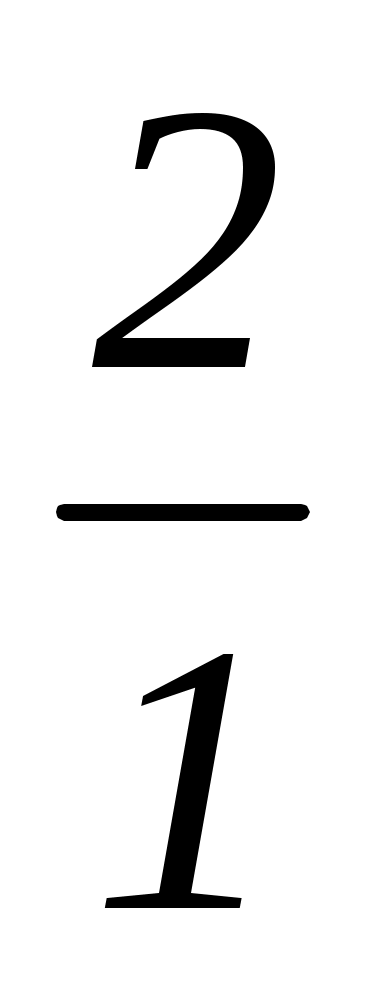 = 3;
= 3;
Если y = 3, то x = 5 –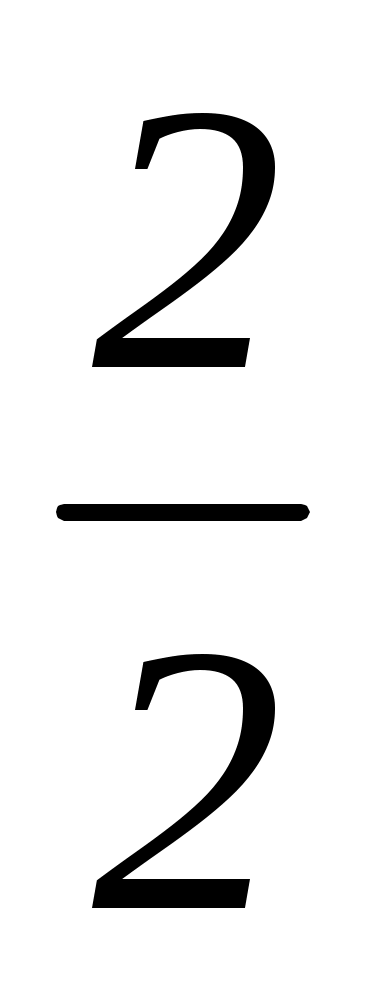 = 4.
= 4.
Ответ: x1 = 6; y1 = –1;
x2 = 7; y2 = 0;
x3 = 3; y3 = 2;
x4 = 4; y4 = 3.
Чуть позже, когда будут изучены формулы сокращенного умножения, можно предложить следующие задачи:
Решение: x (a2 – 1) = a + 1 – x (a + 1);
((a2 – 1) + (a + 1)) x = a + 1;
(a2 + a) x = a + 1;
a (a + 1) x = a + 1.
x =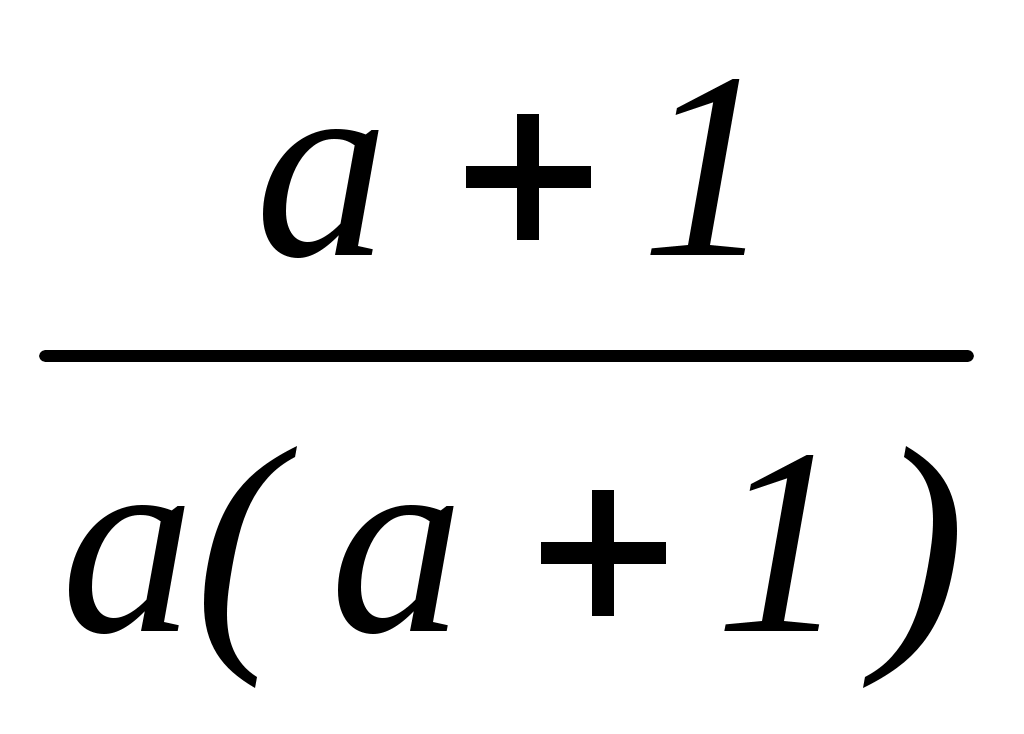 ; x =
; x =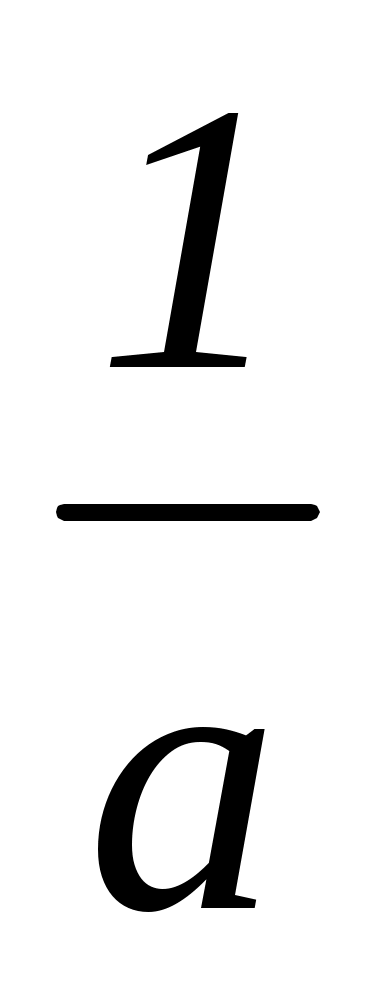 .
.
2. а) Если a = 0, то 0 x = 1, корней нет.
б) Если a = –1, то 0 x = 0, x – любое число.
Ответ: при a 0, a –1 x =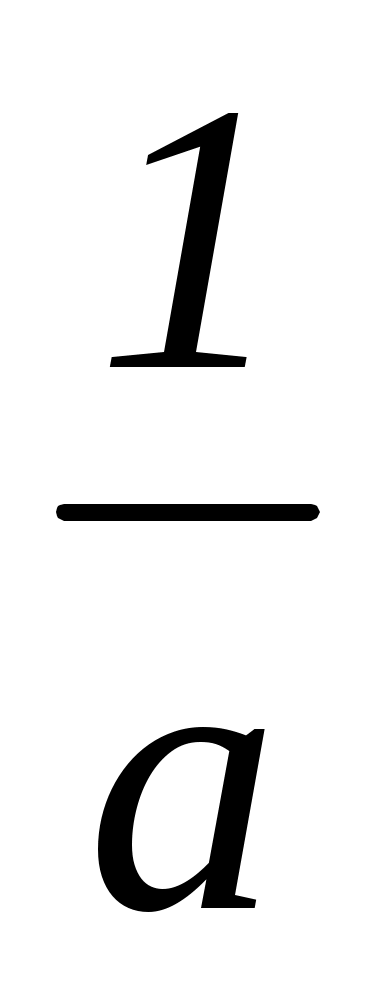 ;
;
при a = 0 корней нет;
при a = –1 x – любое число.
а) имеет единственный корень;
б) имеет бесконечное множество корней;
в) не имеет корней?
а) n (x – 1) = n2 + n + 1
Ответ: при n = 1.
б) n (x + 5) = n2 + n + 4
Так как меньшее число учащихся может быть в 7-м и 9-м классах, то должны выполняться неравенства 36 –
Из того, что числа 36 –
Учитывая эти два условия (n 9 и nкратно 3), заключаем, что nравно 3, 6 или 9.
Поэтому окончательный ответ на вопрос задачи мы можем записать так: в 7-м классе было 36 –
Иначе говоря, возможны три варианта: в 7-м, 8-м и 9-м классах могло быть соответственно 35, 38, 32; или 34, 40, 31; или 33, 42, 30 учащихся.
Задача очень объемная. Цель ее рассмотрения:
-
показать, как "рождаются" задачи с параметрами; -
зависимость ответа от значения параметра;
Поэтому целесообразно первую часть разобрать в форме диалога с учащимися, а далее конструктивно перейти к ответу, акцентировать внимание на возможных значениях n. Непосредственно закончить решение задачи предлагается самостоятельно по желанию, с последующим выставлением оценки в журнал, либо разобрать на факультативном занятии.
Во вводной беседе следует заметить, что изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Наиболее трудной и важной частью решения таких задач является исследование процесса в зависимости от параметров.
Формированию некоторых навыков решения таких задач и посвящена данная тема.
Итак, решение линейного уравнения
ax = b в общем виде, исследование количества его корней в зависимости от значений параметра относится к задачам с параметром.
Решим ряд устных упражнений типа:
-
Дано уравнение ax = 3a + 8.
Какое уравнение получится при а) a = 10; б) a = 2;
в) a = ¼; г) a = 0.
-
Является ли уравнение 2ax (a – 1) + a = 4x – 8a линейным
а) относительно x;
б) относительно a.
-
Дано уравнение ax = 4x + 5.
Найдите множество корней этого уравнения в случае, если a = 4, a 4.
После этого восстановим схему решения линейного уравнения ax = b (x – переменная, a, b – некоторые числа). Для этого можно пригласить к доске сильного ученика.
 ax = b
ax = b

a 0, b – любое a = 0
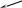
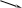
x = b = 0b 0
0 x = 0 0 x = b
x – любое числокорней нет
Однако, учитывая, что решение задачи обычно записывается не блок-схемой, предпочтительно знакомить учащихся со словесным алгоритмом решения. Его они и записывают в тетрадь вслед за учителем.
Алгоритм решения линейных уравнений с параметром.
Ax = B (x – неизвестное,
A, B – выражения, зависящие только от параметров)
-
Если A 0, то x =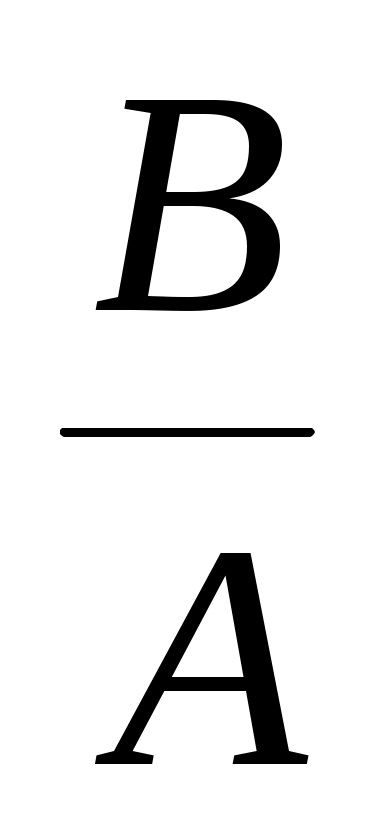 .
.
Уравнение имеет один корень, причем x 0, если a 0 и b 0 или a 0 и b 0;
x = 0, если b = 0;
x 0, если a 0 и b 0 или a 0 и b 0.
-
а) Если A = 0, B = 0
0 x = 0, x – любое число.
Уравнение имеет бесконечно много корней.
б) Если A = 0, B 0
0 x = B, корней нет.
Уравнение корней не имеет.
Сначала прорешиваем ключевые уравнения, акцентируя внимание на правильную запись ответа.
-
ax = 10
Решение: а) Если a 0, то x =
б) Если a = 0, то 0 x =10, корней нет.
Ответ: при a 0 x =
при a = 0 корней нет.
-
0 x = a
Решение: а) Если a = 0, то 0 x = 0, x – любое число;
б) Если a 0, то 0 x = a, корней нет.
Ответ: при a = 0 x – любое число;
при a 0 корней нет.
Обращаем внимание, что значение коэффициента известно, буквой a обозначен свободный член. При решении данного уравнения работает второй шаг алгоритма.
-
2m (m – 2) x = m – 2
Решение: 1. Если 2m (m – 2) 0, то m 0, m 2;
x =
2. а) Если m = 0, то
(на первых порах записываем подробно, чтобы ученики видели источник появления уравнения)
2 0 (0 – 2) x = 0 – 2,
0 x = – 2,
корней нет.
б) Если m = 2, то
2 2 (2 – 2) x = 2 – 2,
0 x = 0,
x – любое число.
Ответ: при m 0, m 2 x =
при m = 0 корней нет;
при m = 2 x – любое число.
-
ax + 3 = 4a – 2x
Решение: Преобразуем уравнение к виду ax = b.
ax + 2x = 4a – 3,
(a + 2) x = 4a – 3.
1. Если a + 2 0, то a –2, x =
2. Если a = –2, то (–2 + 2) x = 4 (–2) – 3,
0 x = –11,
корней нет.
Ответ: при a –2 x =
при a = –2 корней нет.
-
При каком значении параметра а уравнение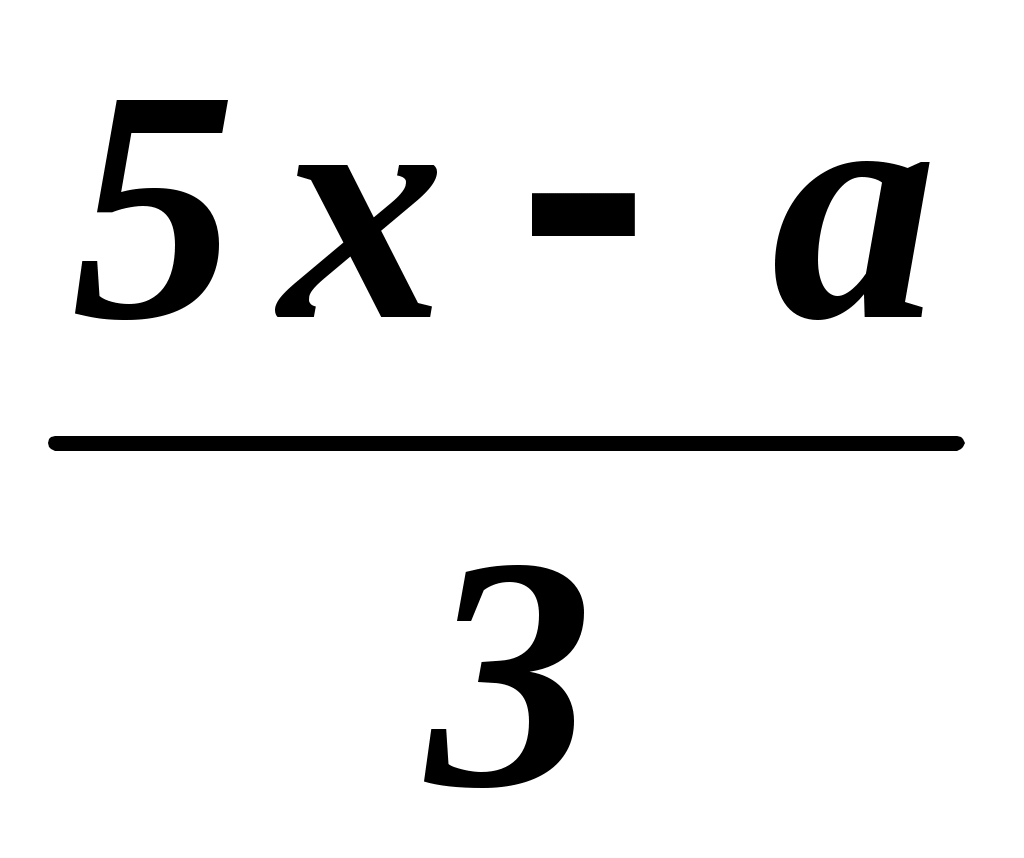 =
= 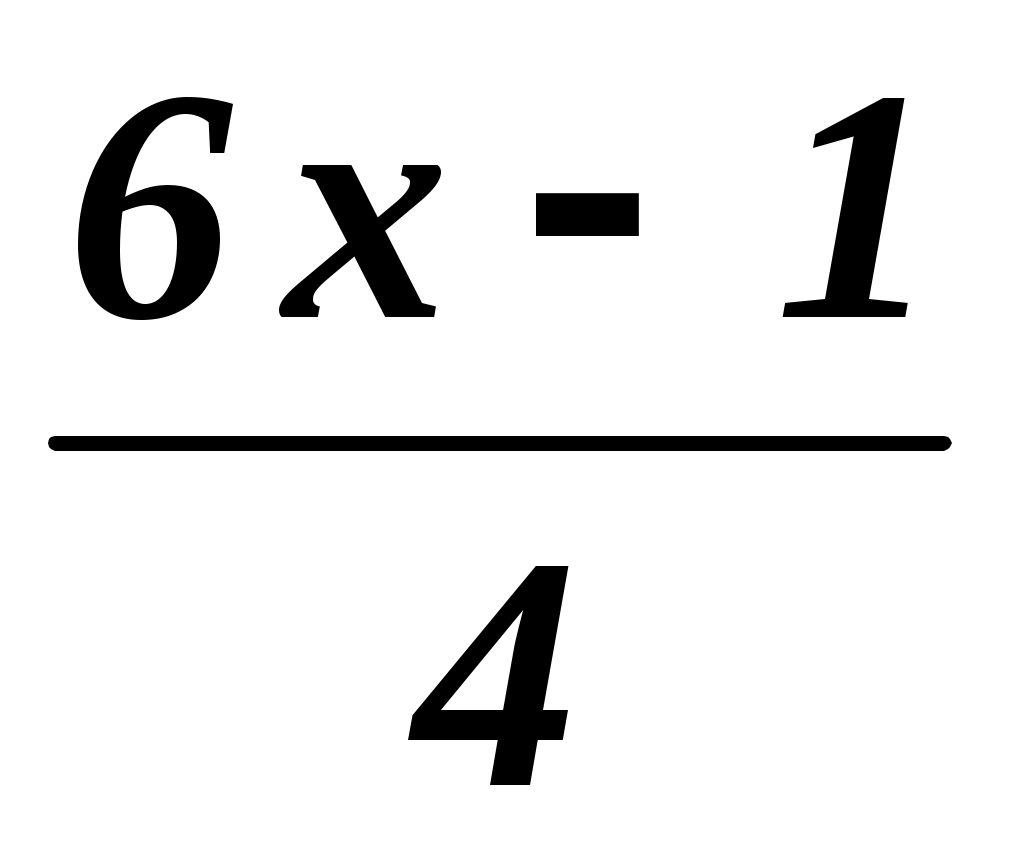 имеет корень:
имеет корень:
а) больший нуля; б) меньший нуля; в) равный нулю?
Решение:
Умножим обе части уравнения на 12:
20x – 4a = 18x – 3;
20x – 18x = 4a – 3;
2x = 4a – 3;
x =
x = 2a – 1,5.
а) x 0, если 2a – 1,5 0, 2a 1,5, a 0,75;
б) x 0, если 2a – 1,5 0, 2a 1,5, a 0,75;
в) x = 0, если 2a – 1,5= 0, 2a = 1,5, a = 0,75.
Ответ: при a 0,75 x 0;
при a 0,75 x 0;
при a = 0,75 x = 0.
Далее учащиеся решают блок задач на отработку задач типа 15. Такие задачи составляются весьма легко.
Разные задачи
-
Составить линейное уравнение, обе части которого содержат параметр a так, чтобы уравнение имело решение при любом действительном a.
Ответ: (a2 + 1) x = a или ax = a
-
При каком целом неотрицательном значении n имеет целые корни уравнение
Решение: Умножим обе части уравнения на 9:
4n – 6 – 3 (x – 2) = 9;
4n – 6 – 3x + 6 = 9;
–3x = 9 – 4n;
x =
x =
Уравнение имеет целые корни, если 4n – 9 кратно числу 3, следовательно, 4n кратно числу 3, отсюда n = 3k, где k – натуральное число.
Ответ: n = 3k, k N.
-
Решить уравнение x – xy + 5y = 7в целых числах.
Решение: Решим это уравнение относительно x, т.е. букву y будем считать параметром. Имеем:
x – xy = 7 – 5y;
x (1 – y) = 7 – 5y;
x =
Выделим из дроби
Итак, x = 5 –
Вычислим соответствующие значения x:
Если y = –1, то x = 5 –
Если y = 0, то x = 5 –
Если y = 2, то x = 5 –
Если y = 3, то x = 5 –
Ответ: x1 = 6; y1 = –1;
x2 = 7; y2 = 0;
x3 = 3; y3 = 2;
x4 = 4; y4 = 3.
Чуть позже, когда будут изучены формулы сокращенного умножения, можно предложить следующие задачи:
-
Решить относительно x уравнение x (a2 – 1) = (a + 1) (1 – x).
Решение: x (a2 – 1) = a + 1 – x (a + 1);
((a2 – 1) + (a + 1)) x = a + 1;
(a2 + a) x = a + 1;
a (a + 1) x = a + 1.
-
Если a (a + 1) 0, то a 0, a –1
x =
2. а) Если a = 0, то 0 x = 1, корней нет.
б) Если a = –1, то 0 x = 0, x – любое число.
Ответ: при a 0, a –1 x =
при a = 0 корней нет;
при a = –1 x – любое число.
-
При каких значениях параметра n уравнение (n2 – 4) x = n3 – 2n2 – n + 2 :
а) имеет единственный корень;
б) имеет бесконечное множество корней;
в) не имеет корней?
-
Зная, что n N, выясните, имеет ли заданное уравнение целые решения и, если имеет, то при каких n:
а) n (x – 1) = n2 + n + 1
Ответ: при n = 1.
б) n (x + 5) = n2 + n + 4