Файл: Александры Анатольевны.doc

Ответ: при n = 1, n = 2, n = 4.

12. 
    При каких значениях параметра p уравнение px (px + 3) + 6 = x (px – 6)является линейным?
    

При решении текстовых задач, содержащих параметры, приходится учитывать допустимые значения параметра, определяемые смыслом задачи. Иногда границы, в которых заключены значения параметра, приходится устанавливать, исходя из реального смысла задачи.

13. 
    На улице 24 дома, которые имеют 12, 16 и 17 этажей. При этом 17-этажных домов в 2 раза больше, чем 16-этажных, а 12-этажных – на n меньше, чем 16-этажных домов. Сколько разных типов домов на улице?
    

Решение: Пусть x – число 16-этажных домов. Тогда 2x – число 17-этажных домов, а x – n – число 12-этажных домов. Имеем уравнение:

x + 2x + x – n = 24;

4x = 24 + n;

x = ;

x = 6 + .

По смыслу задачи nN, следовательно,(x – n) также натуральное число и n кратно 4. Это возможно лишь при n = 4. Отсюда x = 7, 2x = 14, x – n = 3.

Ответ: четырнадцать 17-этажных домов,

семь 16-этажных и

три 12-этажных дома.

14. 
    Квадрат суммы двух последовательных натуральных чисел больше суммы их квадратов на 2n. Найти эти числа для значения параметра n из промежутка
    

50  n  100.

Решение: Пусть x – меньшее число; тогда следующее число x + 1. Их сумма равна 2x + 1, а сумма их квадратов x² + (x + 1)² = 2x² + 2x + 1. По условию:

(2x + 1)² – (2x² + 2x + 1) = 2n;

x (x + 1) = n.

Поскольку x  N, n  N и 50  n  100, то это уравнение проще всего решить подбором.

Уравнению с дополнительными ограничениями удовлетворяют числа 7, 8 и 9.

Ответ: 7 и 8, или 8 и 9, или 9 и 10.

15. 
    Сумму a выплатили 5-рублевыми и 10-рублевыми монетами, причем тех и других выдали поровну. Сколько было выдано 5-рублевых монет?
    

Ответ: , где a – число, кратное 15.

16. 
    Отец старше сына в n раз, а его дочь моложе брата в 2 раза. Сколько лет отцу, сыну и дочери, если отец старше дочери на 28 лет?
    

Ответ: отцу 32 года, сыну 8 лет, дочери 4 года.

17. 
    Произведение двух последовательных натуральных чисел больше их суммы на a, где a – двузначное число, большее 50. Найдите эти числа.
    

---

Ответ: 8 и 9, или 9 и 10, или 10 и 11.

Очевидно, что предложенные задачи являются нестандартными для семиклассников, поэтому некоторые из них выполняются в классе как дополнительные к уроку, некоторые рассматриваются на кружке или предлагаются для долгосрочного домашнего задания.

Изучение темы "Системы линейных уравнений" можно разнообразить содержанием таких параметрических задач:

18. 
    При каких значениях b имеют общий корень уравнения:
    

а) 3x + 7 = 0 и 2x – b = 0;

б) 2x = 3b – 1 и 3x = 5b + 7?

Ответ: а) –4 ; б) –17.

19. 
    При каких значениях a и b система уравнений
    

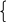
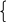а) 3x – 5y = a, б) ax + by = 2,

2x + y = b; 5x + by = 3 + a

имеет решение x = 3, y = –1.

Ответ: а) a = 14, b = 5; б) a = 3,5 , b = 8,5.

20. 
    При каких значениях a и b прямая y = ax+ b проходит через точки M(1;5) и N(-5;-3)?
    

Ответ: a = 1 ; b = 3 _.

21. 
    При каких значениях a и b системе уравнений
    

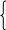3x + 2y = 15a,

x + y = 9

удовлетворяет пара равных чисел? Для каждого такого a найдите решение системы.

Ответ: a = 2, x = y = 6.

При повторении материала в конце года можно познакомить учащихся с различными способами решения уравнений с параметром.

22. 
    Сколько решений имеет уравнение  x  = a в зависимости от параметра a?
    

Решение: Аналитический способ.

Используя определение модуля действительного числа, заключаем:

1. 
   При a  0 уравнение имеет два корня: x = –a, x = a.
   
2. 
   При a = 0 уравнение имеет один корень: x = 0.
   
3. 
   При a  0 уравнение не имеет корней.
   

Графический способ.

Построим графики функций y =  x и y = a.

---

y


y =  x 



y = a (a  0)


y = a (a = 0)

О
y = a (a  0)

0

x
чевидно, что:

1. 
   при a  0 графики пересекаются в двух точках (–a, a) и (a, a), значит, уравнение имеет два корня: x = –a, x = a;
   
2. 
   при a = 0 точка пересечения одна – начало координат, следовательно, уравнение имеет один корень: x = 0.
   

3. 
   при a  0 графики функций не пересекаются – корней нет.
   

Ответ: при a  0 два корня;

при a = 0 один корень;

при a  0 корней нет.

23. 
    Решить уравнение ax =  x .
    

Решение: Аналитический способ.

1. 
   При x  0 x =  x , следовательно, исходное уравнение равносильно уравнению ax = x,
   

(a – 1) x = 0.

а) Если a – 1  0, a  1, x = 0;

б) Если a – 1 = 0, a = 1, 0 x = 0, x – любое число, большее или равное 0 (x  0).

2. 
   При x  0  x  = – x, уравнение равносильно уравнению
   

ax = –x,

(a + 1) x = 0.

а) Если a + 1  0, a  –1, x = 0;

б) Если a + 1= 0, a = –1, 0 x = 0, x – любое число, меньшее или равное 0 (x  0).

Графический способ (1).

Построим графики функций y =  x и y = ax.

Графиками функций y = ax являются прямые, проходящие через начало координат, угловой коэффициент которых равен a.


A


y = ax (a1)

y =  x 

y

---

B

0


y = ax (a0)

x


y = x


y = –x

1. 
   При a  –1 уравнение имеет один корень: x = 0.
   
2. 
   При a = 1 прямая y = ax (y = x) содержит луч OA, и уравнение имеет бесконечно много корней: x  0.
   
3. 
   При a = –1 прямая y = ax (y = –x) содержит луч OB, и уравнение имеет беско-нечно много корней: x  0.
   

Графический способ (2).

Данное уравнение для любого значения параметра a всегда имеет, по крайней мере, одно решение x = 0, т.к. графики функций y =  x и y = ax при любых значениях параметра a имеют общую точку – начало координат.

Пусть x  0. Выразим из уравнения ax =  x параметр a через x: a = и построим графики функций: y = a и y = . Используя определение модуля, получим:


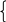
–1, при x  0,

1, при x  0


y


1


y = 1


y = –1

–1

y = a (a  1)

y = a (–1 a 0)

---

0

x


y = a (a –1)

1. 
   При a  1 графики не имеют общих точек, следовательно, корней уравнения кроме x = 0, нет.
   
2. 
   При a = 1 график функции y = a (y = 1) содержит правую часть графика функции y = (x  0), следовательно,уравнение имеет бесконечно много корней: x  0 (учитываем, что x = 0 при любых a).
   
3. 
   При a = –1 график функции y = a (y = –1) содержит левую часть графика функции y = (x  0), и уравнение имеет бесконечно много корней: x  0.
   

Ответ: при a  1 x = 0;

при a = 1 x  0;

при a = –1 x  0.

Это упражнение является очень полезным, т.к. во многих случаях графический метод более уместен, чем аналитический, а на первых порах следует рассматривать все способы, чтобы выработать у учащихся зоркость в выборе метода решения более сложных задач.

Итак, все рассмотренные выше упражнения (123) и им подобные имеют ясную дидактическую цель – помочь учащимся составить представление о параметре, о том, что значит решить уравнение с параметром.

Учащиеся 7 класса должны усвоить главное: параметр, будучи фиксированным, но неизвестным числом, имеет как бы двойственную природу. Во-первых, предполагаемая известность позволяет "общаться" с параметром как с числом, а во-вторых, степень свободы общения ограничивается его неизвестностью. Так, деление на выражение, содержащее параметр, требует дополнительного исследования. Как правило, результаты этих исследований влияют и на решение, и на ответ.

При решении задач с параметром учитель должен обратить внимание учащихся на необходимость осторожного, деликатного обращения с фиксированным, но неизвестным числом.

К концу года учащиеся должны уметь решать задачи типа 16, 9, 10, 18, 19. Регулярно в проверочные и контрольные работы последними заданиями включаются задачи с параметрами.

В мае проводится контрольная работа, в которую включены все типы основных задач, однако уровень сложности зависит непосредственно от контингента учащихся.

---