ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 123
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
).
Для закрепления решаем задачи:
Решение: px2 + (3p + 1)x 4p 0;
(3p + 1)2 4p 4р 0; 7р2 6р 1 0; (р +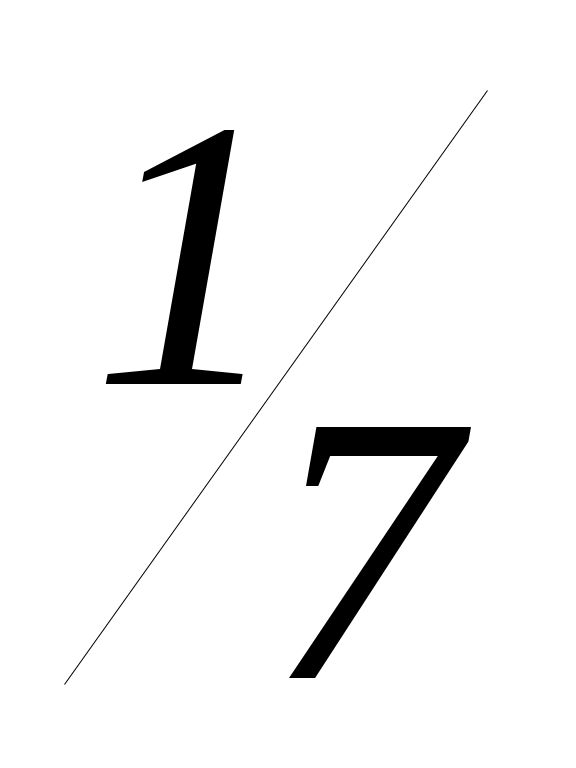 )(р 1) 0;
)(р 1) 0;
Ответ: (; 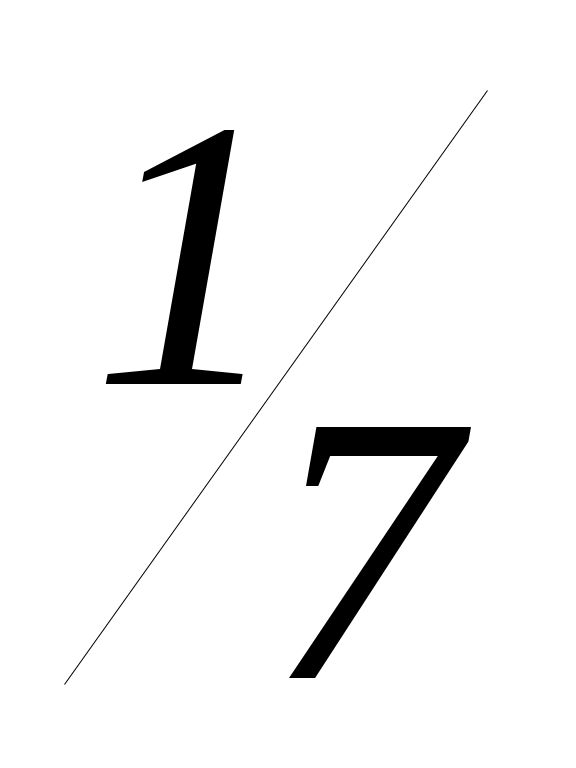 ].
].
Ответ: [2; +).
Ответ: (; 0,4).
Ответ: (1; +).
При работе над этими задачами рекомендую выполнять графическую иллюстрацию, которая зачастую сразу помогает понять суть задачи.
Приступая к решению квадратных неравенств, говорим, что предыдущая группа задачи с дополнительными условиями. Мы искали значения параметров, удовлетворяющих конкретным требованиям.
Если же следует решить неравенство, значит, оно должно быть рассмотрено при всех значениях параметра. Если хотя бы одно значение не исследовано, решение задачи не может быть признано полным. При решении неравенств используем таблицу, чтобы не пропустить все возможные случаи.
В 9 классе достаточно рассмотреть несколько примеров, где первый коэффициент не зависит от параметра.
Решить неравенства:
а = 1, а 0;
D1 = 1 a;
x1 = 1 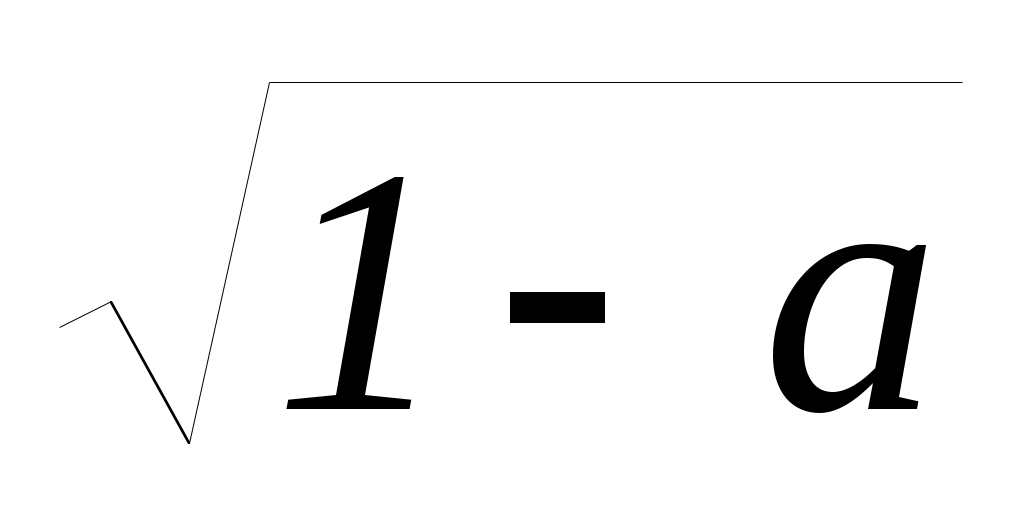 ; x2 = 1 +
; x2 = 1 +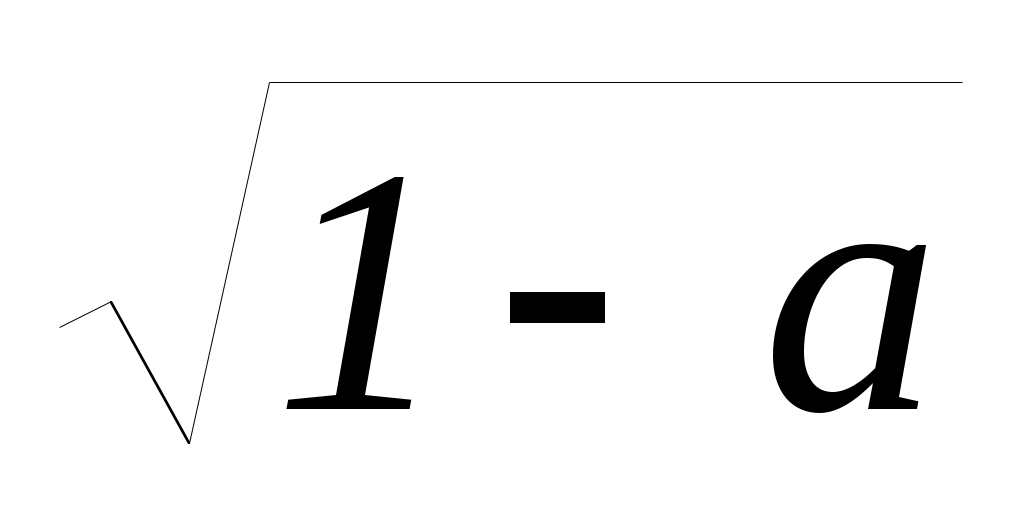 ;
;
х 1 +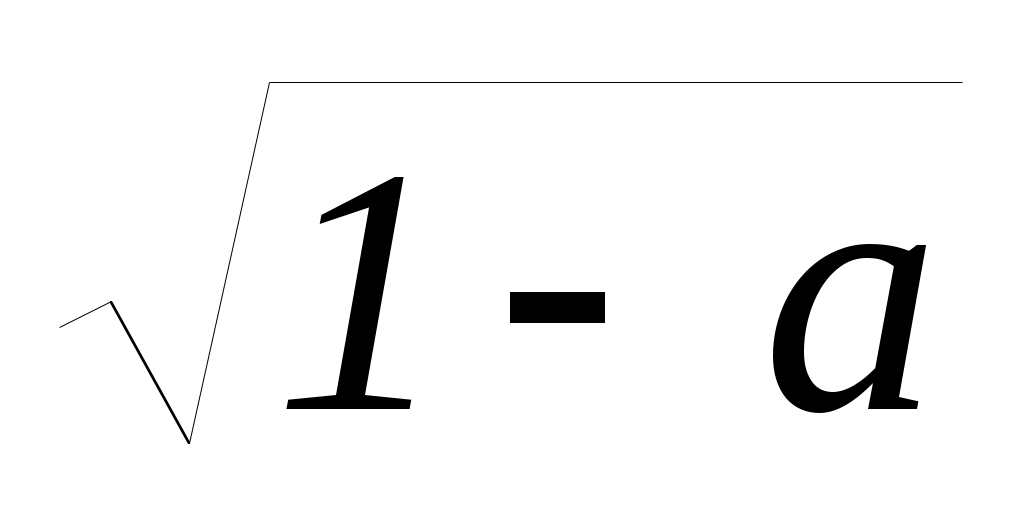 .
.
х 1.
Ответ: при а (; 1) х (; 1 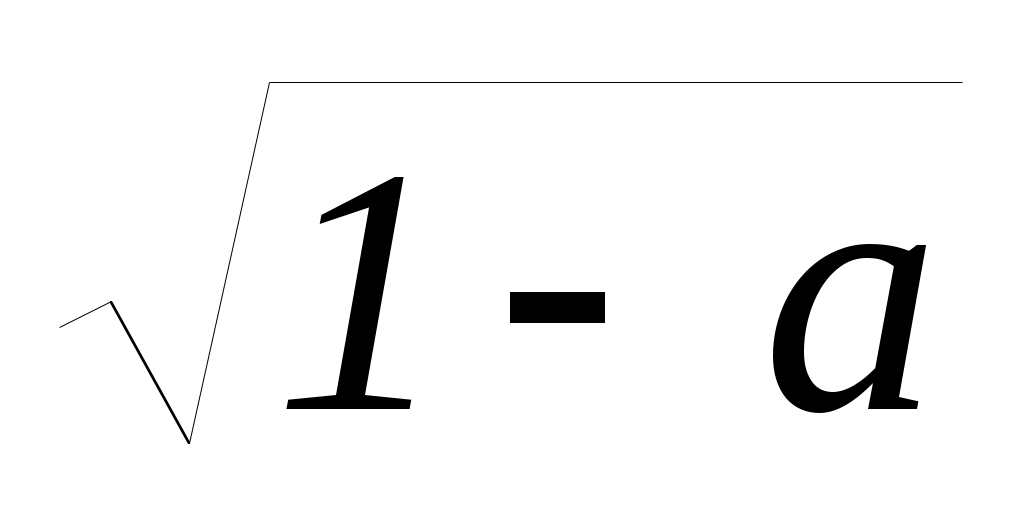 ) U (1 +
) U (1 +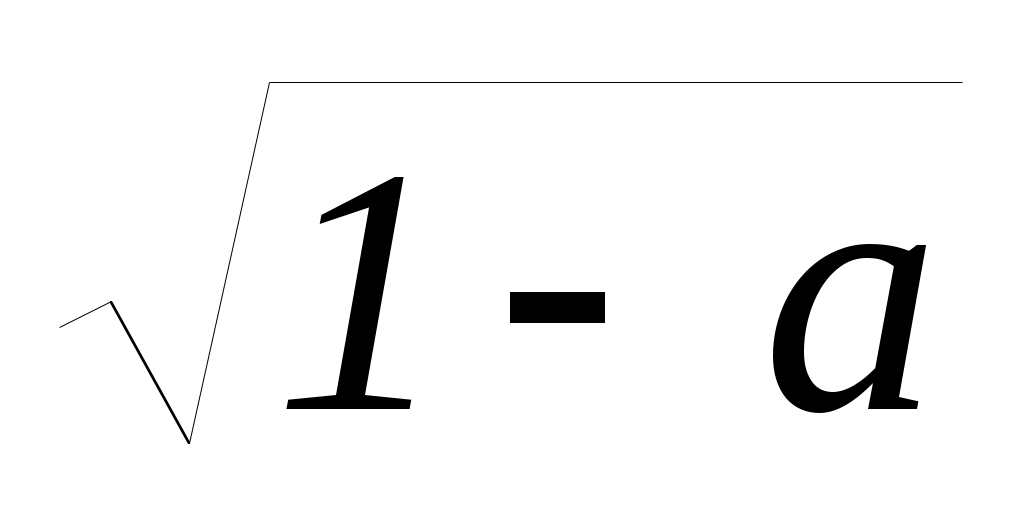 ; +);
; +);
при а = 1 х (; 1) U (1; +);
при а (1; +) х R.
Аналогичное неравенство:
D = 9а (а +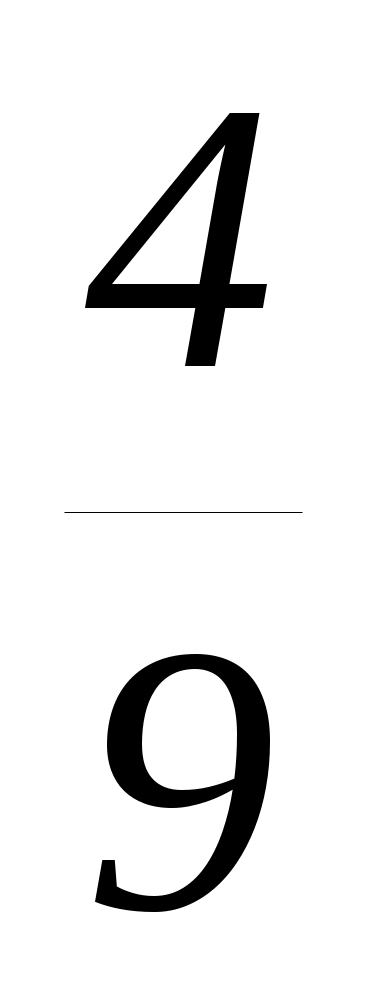 ), поэтому следует рассмотреть случаи:
), поэтому следует рассмотреть случаи:
а = 1, а 0;
D1 = (a + 2)2;
Ответ: при а = 2; х = 2;
при а 2 решений нет.
х2 + ах + 1 0;
а = 1; а 0;
D= а2 4;
х1 =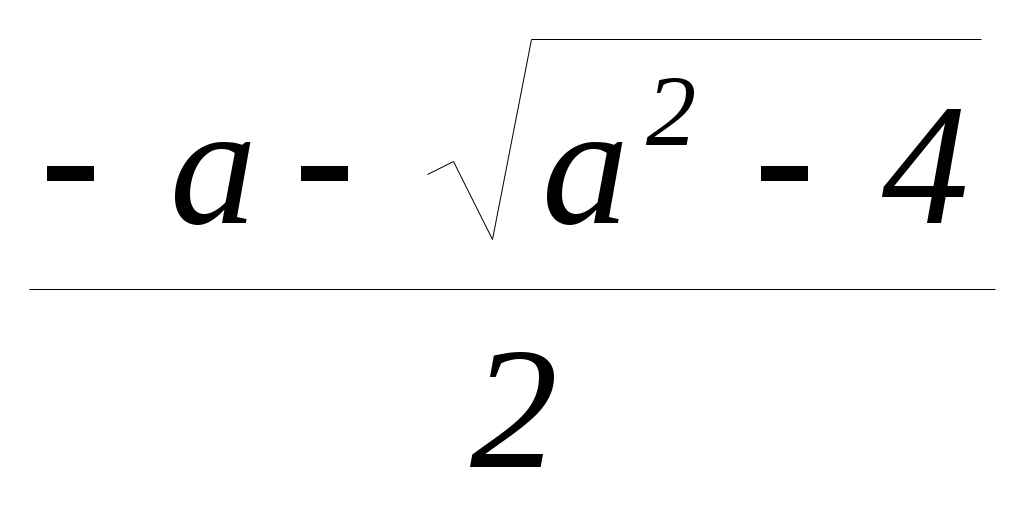 ; х2 =
; х2 = 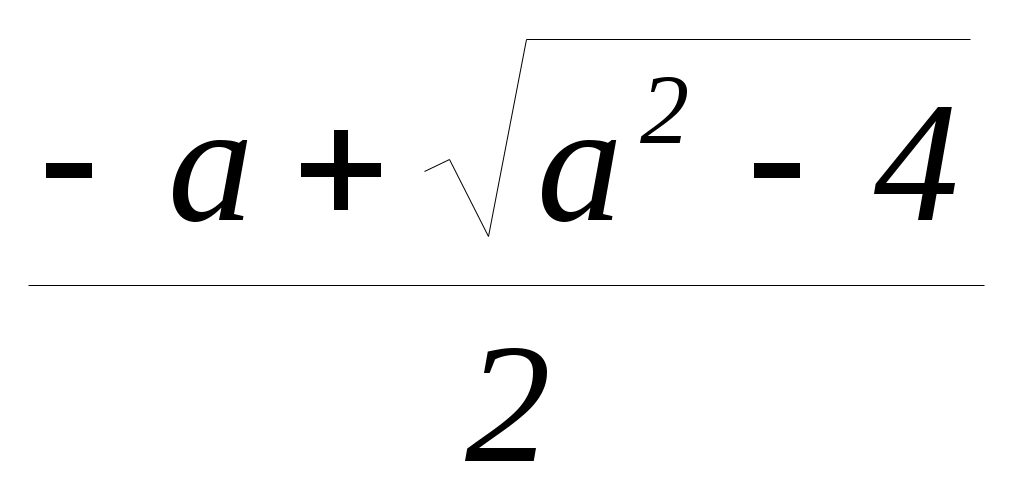 ;
;
а 2;
б) а = 2, (х + 1)2 0, х R\{1}
Ответ: при а 2; х 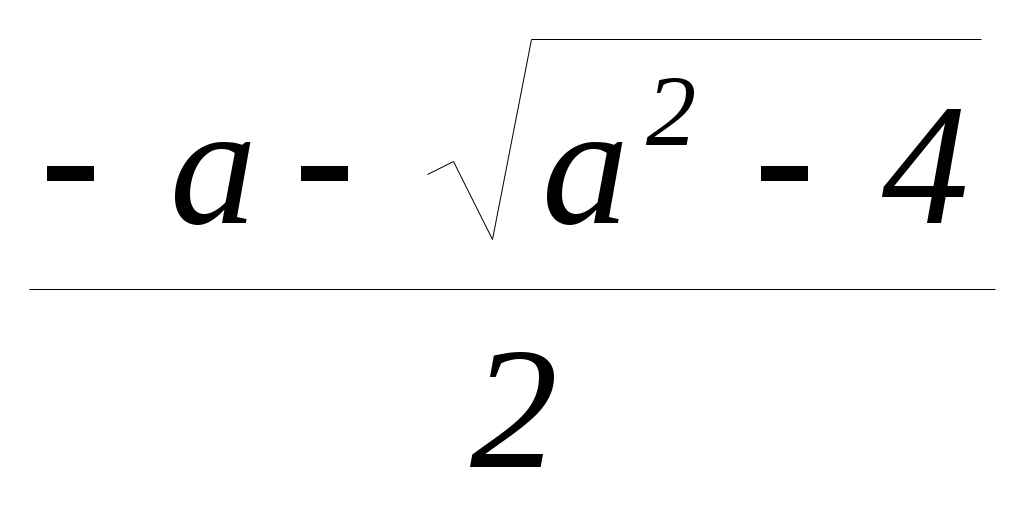 или х
или х 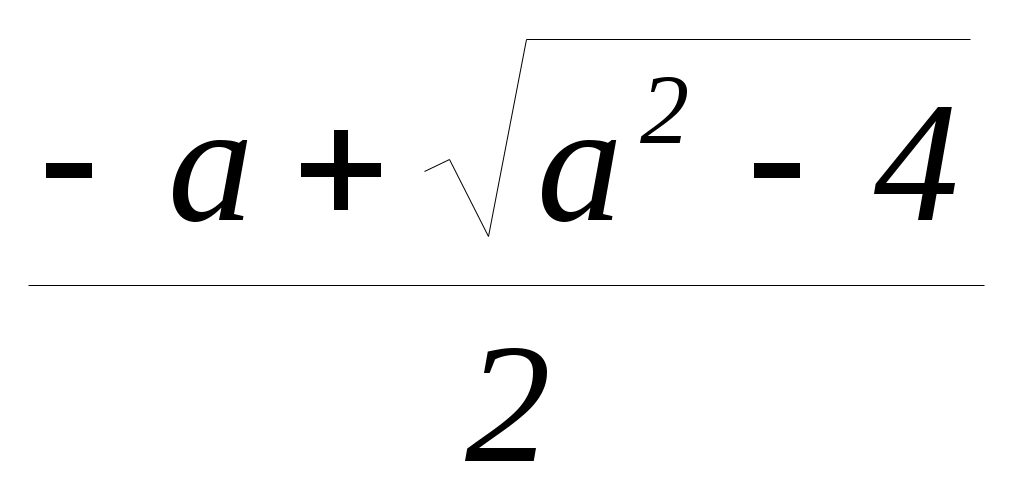 ;
;
при а 2; х R;
при а = 2; х R\{1};
при а = 2; х R\{1}.
Используются различные формы записи решения неравенства, важным является приучить школьников к последовательности в решении и выписке ответа.
Ключевыми задачами этой темы являются задачи 71, 72, 78, 80, 85.
На этапах изучения можно предлагать самостоятельные работы из 1-2 задач, а по завершении темы, учитывая определенную ее сложность домашнюю контрольную работу по ключевым задачам.
Расположение корней квадратного трехчлена
на числовой оси.
Изучение этого вопроса закладывает базу для решения тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств с параметрами. Во многих случаях эти решения приводят к громоздким преобразованиям. В то же время использование свойств квадратичной функции позволяет существенно упростить решение.
Кроме того, решение многих задач с параметрами, предлагающихся на вступительных экзаменах в вузы, требует умения правильно формулировать необходимые и достаточные условия, связанные с расположением корней квадратного трехчлена относительно некоторых характерных точек.
Основное внимание уделено наглядности, обоснование утверждений существенно опирается на чертеж.
У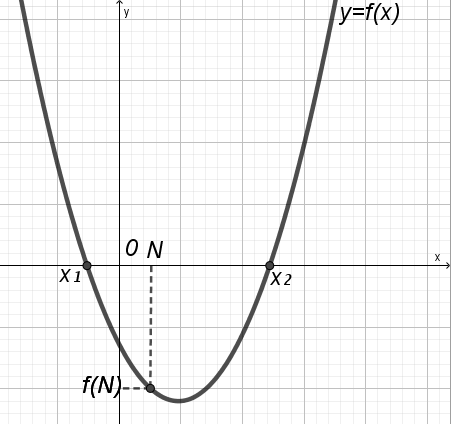 тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1 N х2), необходимо и достаточно выполнение неравенства
тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1 N х2), необходимо и достаточно выполнение неравенства
А f(N) 0
Доказательство:
Nx1 0; Nx2 0;
(N x1)( N x2) 0;
N2 x1N x2N + x1 x2 0;
N2 (x1 + x2)N + x1 x2 0;
N2 +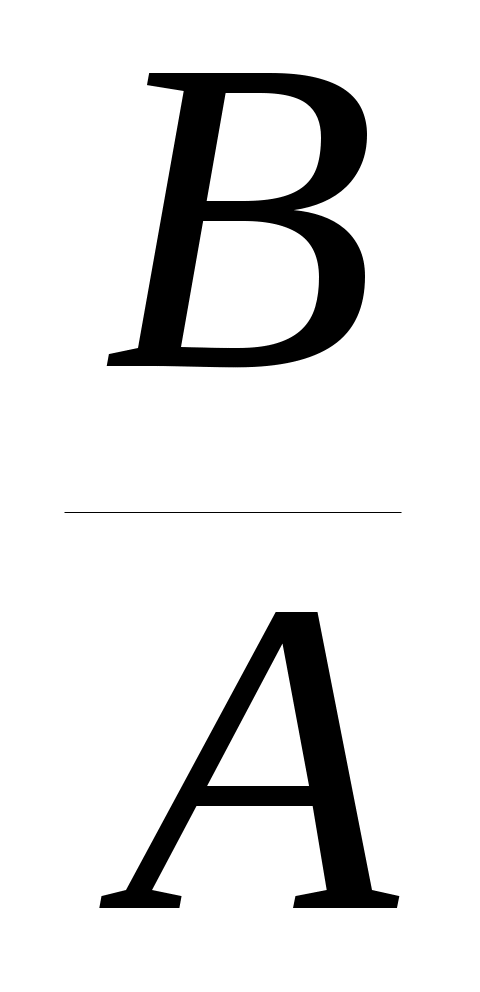 N +
N + 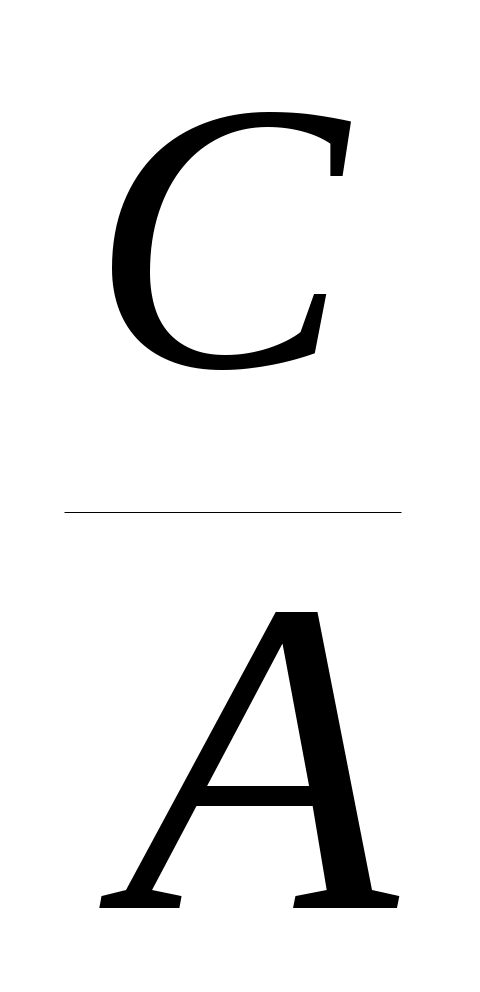 0 xa2;
0 xa2;
A (AN2 + BN + C) 0;
a f(N) 0.
Решение: А f(2) 0;
A = 1; f(2) = 4 (2m + 1) 2 + 3m 4 = m 2;
m 2 0; m2.
Ответ: m2.
Эту задачу можно переформулировать так: при каких m число 0 лежит между корнями уравнения?
Решение: А = m; f(0) = m 3;
m(m 3) 0; 0 m 3.
Ответ: (0; 3).
Замечание: Эту задачу можно решить и используя теорему Виста ( 0).
0).
Решение: А = k2 2;
f(k) = (k2 2)k2+ (k2+ k 1)kk3 + k2 =
= (k2 2) ((k2 2)k2+ (k2+ k 1)k k3 + k2) 0;

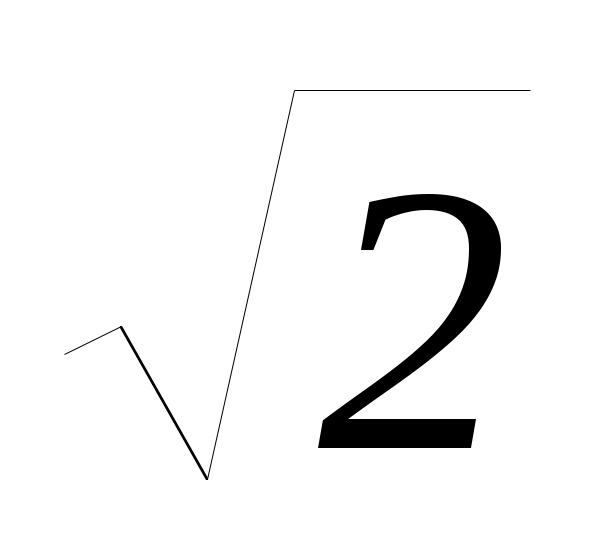 k 0,
k 0,
1 k 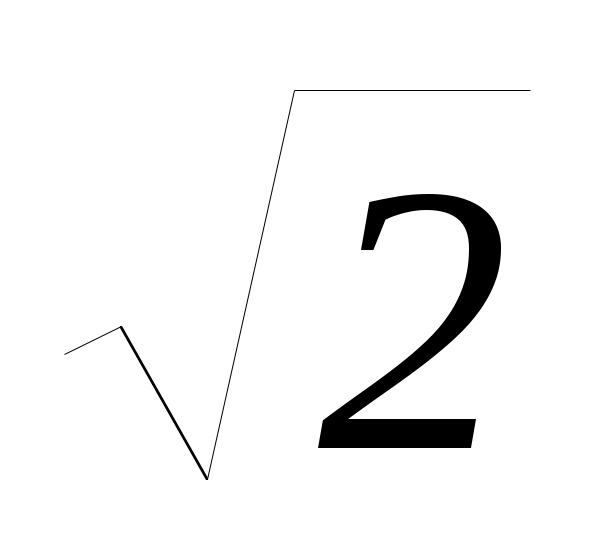
Ответ: (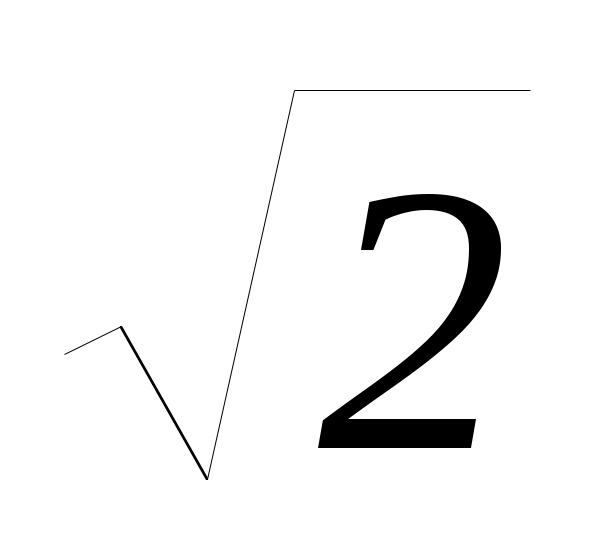 ; 0) U (1;
; 0) U (1;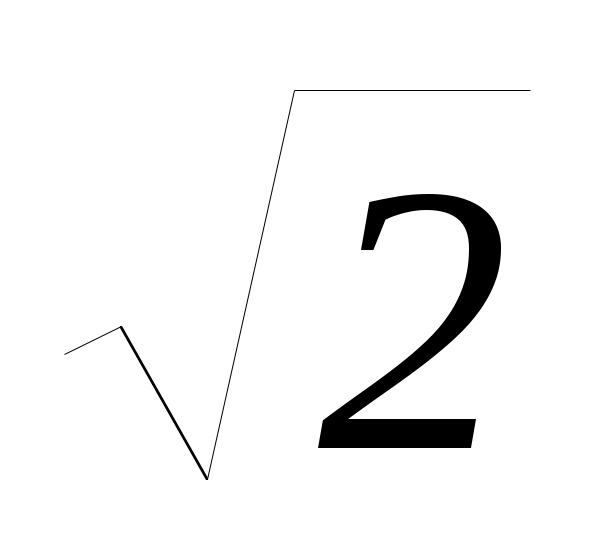 ).
).
У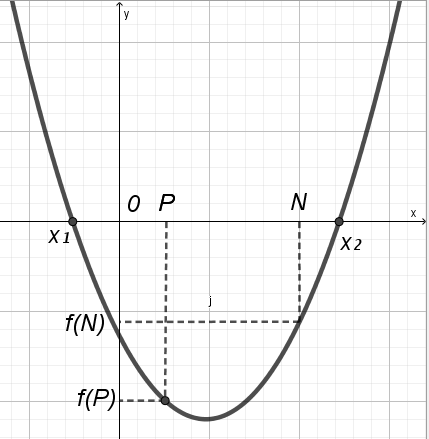 тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий:
тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий:
А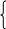 f(N) 0;
f(N) 0;
А f(Р) 0.
Р

 ешение:
ешение:
Для закрепления решаем задачи:
-
При каких значениях р функция y =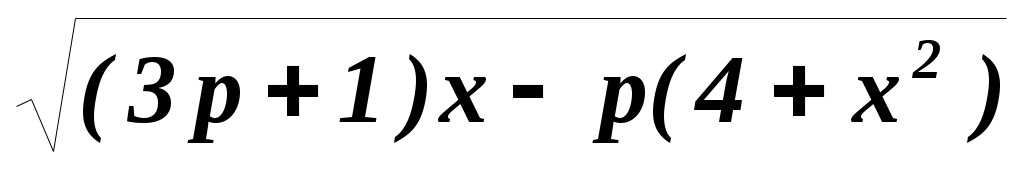 определена при всех действительных значениях х?
определена при всех действительных значениях х?
Решение: px2 + (3p + 1)x 4p 0;
-
p = 0; х 0 не удовлетворяет условию х R. -
р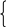
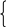
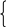 0; p 0, р 0, р 0, р
0; p 0, р 0, р 0, р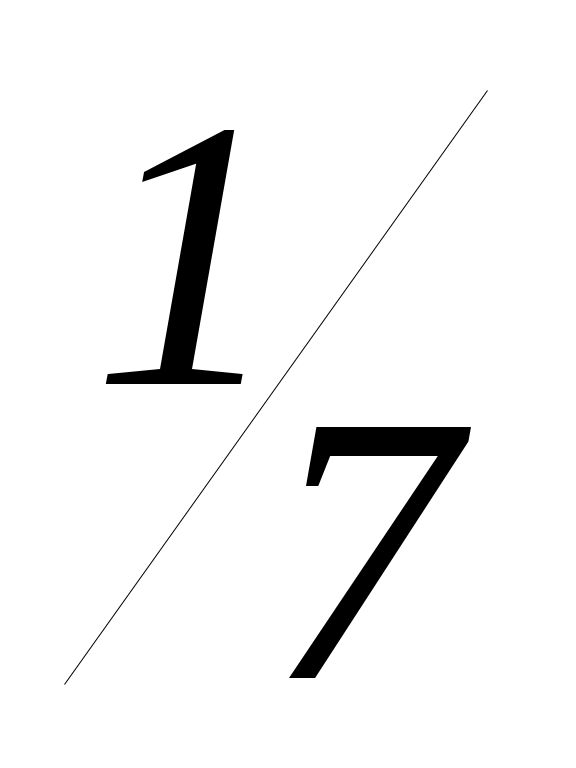
(3p + 1)2 4p 4р 0; 7р2 6р 1 0; (р +
Ответ: (;
-
При каких mнеравенство (m 1)x2 + 2mx + 3m 2 0 не имеет решений?
Ответ: [2; +).
-
При каких nнеравенство (2n2 5n + 2)x2 4nx + 2 0 выполняется при всех х?
Ответ: (; 0,4).
-
При каких а квадратный трехчлен (а2 1) x2 + 2(а 1) x + 1 принимает положительные значения для всех х?
Ответ: (1; +).
При работе над этими задачами рекомендую выполнять графическую иллюстрацию, которая зачастую сразу помогает понять суть задачи.
Приступая к решению квадратных неравенств, говорим, что предыдущая группа задачи с дополнительными условиями. Мы искали значения параметров, удовлетворяющих конкретным требованиям.
Если же следует решить неравенство, значит, оно должно быть рассмотрено при всех значениях параметра. Если хотя бы одно значение не исследовано, решение задачи не может быть признано полным. При решении неравенств используем таблицу, чтобы не пропустить все возможные случаи.
В 9 классе достаточно рассмотреть несколько примеров, где первый коэффициент не зависит от параметра.
Решить неравенства:
-
х2 + 2х + а 0
а = 1, а 0;
D1 = 1 a;
x1 = 1
-
D 1 0; 1a 0; при а 1 х 1
1 0; 1a 0; при а 1 х 1 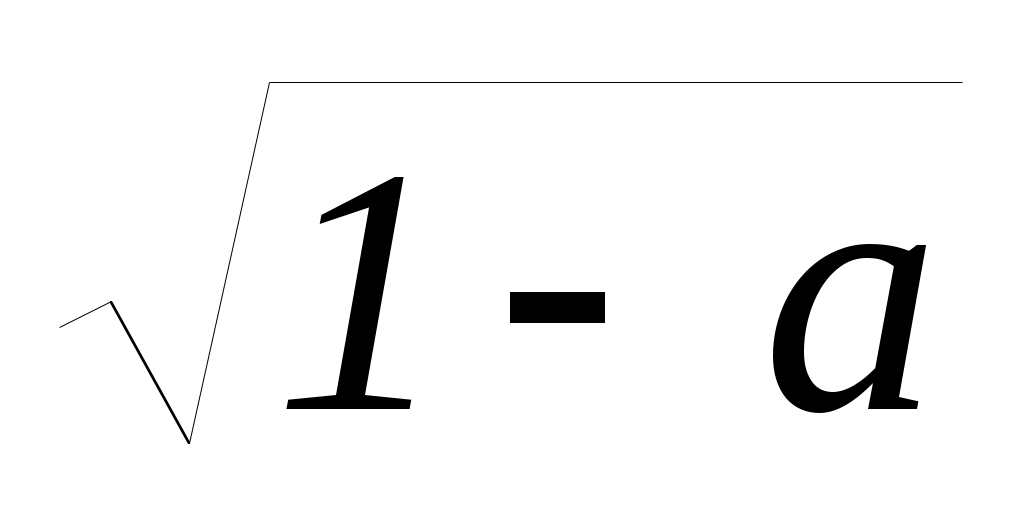 ,
,
х 1 +
-
D 1= 0; 1a = 0; при а = 1 х2 + 2х + 1 0; (х + 1)2 0; х 1,
1= 0; 1a = 0; при а = 1 х2 + 2х + 1 0; (х + 1)2 0; х 1,
х 1.
-
D1 0; 1a 0; при а > 1 х любое число.
Ответ: при а (; 1) х (; 1
при а = 1 х (; 1) U (1; +);
при а (1; +) х R.
Аналогичное неравенство:
-
х2 + 3ах а 0
D = 9а (а +
-
D 0; -
D= 0; a) а = 0; б) а = 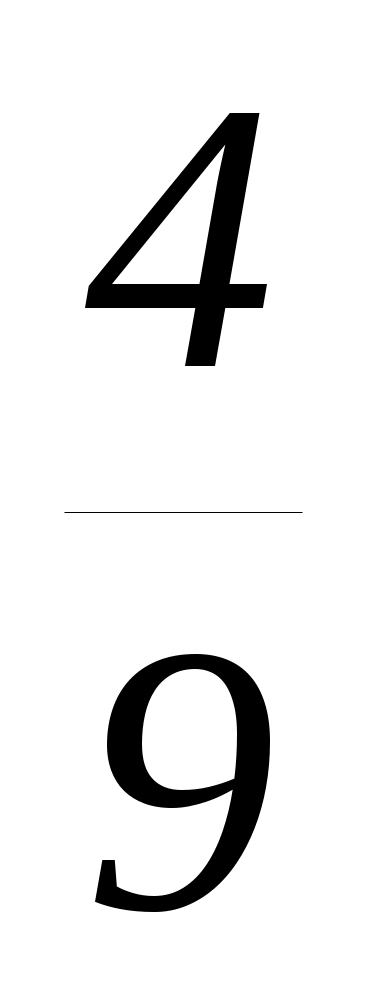 ;
; -
D 0.
-
х2 2ах + 2а2 + 4а + 4 0
а = 1, а 0;
D1 = (a + 2)2;
-
D 0; (а + 2)2 0; таких а нет. -
D= 0 при а = 2; х2 + 4х + 4 0; (х + 2)2 0; х = 2. -
D 0 при а 2; решений нет.
Ответ: при а = 2; х = 2;
при а 2 решений нет.
-
х2 ах + 1
х2 + ах + 1 0;
а = 1; а 0;
D= а2 4;
х1 =
-
D 0; а2 4 0 при а 2, х (; х1) U (х2; +).
0; а2 4 0 при а 2, х (; х1) U (х2; +).
а 2;
-
D= 0; а = 2; а) а = 2, (х 1)2 0, х R\{1}
б) а = 2, (х + 1)2 0, х R\{1}
-
D 0 при 2 а 2, х R.
Ответ: при а 2; х
при а 2; х R;
при а = 2; х R\{1};
при а = 2; х R\{1}.
Используются различные формы записи решения неравенства, важным является приучить школьников к последовательности в решении и выписке ответа.
Ключевыми задачами этой темы являются задачи 71, 72, 78, 80, 85.
На этапах изучения можно предлагать самостоятельные работы из 1-2 задач, а по завершении темы, учитывая определенную ее сложность домашнюю контрольную работу по ключевым задачам.
Расположение корней квадратного трехчлена
на числовой оси.
Изучение этого вопроса закладывает базу для решения тригонометрических, показательных, логарифмических, иррациональных уравнений и неравенств с параметрами. Во многих случаях эти решения приводят к громоздким преобразованиям. В то же время использование свойств квадратичной функции позволяет существенно упростить решение.
Кроме того, решение многих задач с параметрами, предлагающихся на вступительных экзаменах в вузы, требует умения правильно формулировать необходимые и достаточные условия, связанные с расположением корней квадратного трехчлена относительно некоторых характерных точек.
Основное внимание уделено наглядности, обоснование утверждений существенно опирается на чертеж.
-
Пусть квадратный трехчлен f(x) = Ax2 + Bx + Cимеет корни х1 и х2; х0 = 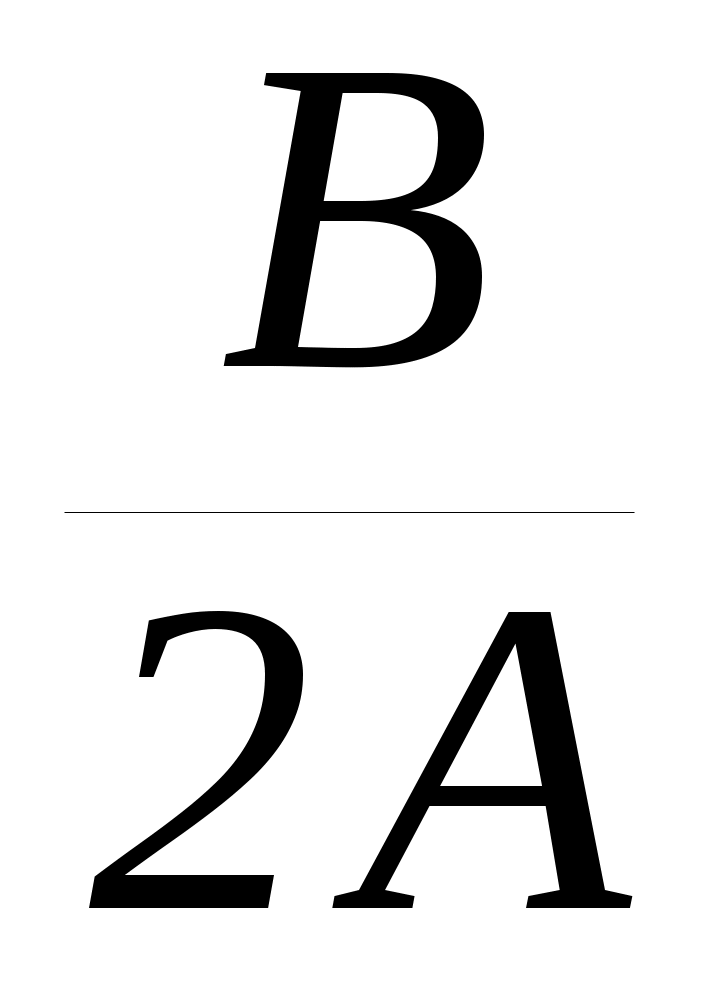 абсцисса вершины параболы; D = B2 4ACдискриминант квадратного трехчлена; M, K, N, P заданные числа.
абсцисса вершины параболы; D = B2 4ACдискриминант квадратного трехчлена; M, K, N, P заданные числа. -
Все чертежи приведены для а 0, случай а 0 рассматривается аналогично.
У
 тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1 N х2), необходимо и достаточно выполнение неравенства
тверждение 1. Для того, чтобы число N было расположено между корнями квадратного трехчлена (х1 N х2), необходимо и достаточно выполнение неравенстваА f(N) 0
Доказательство:
Nx1 0; Nx2 0;
(N x1)( N x2) 0;
N2 x1N x2N + x1 x2 0;
N2 (x1 + x2)N + x1 x2 0;
N2 +
A (AN2 + BN + C) 0;
a f(N) 0.
-
При каких mуравнение x2 (2m + 1)x + 3m 4 = 0 имеет два корня, один из которых меньше 2, а другой больше 2?
Решение: А f(2) 0;
A = 1; f(2) = 4 (2m + 1) 2 + 3m 4 = m 2;
m 2 0; m2.
Ответ: m2.
-
При каких mуравнение mx2 + (3m 2)x + m 3 = 0 имеет корни разных знаков?
Эту задачу можно переформулировать так: при каких m число 0 лежит между корнями уравнения?
Решение: А = m; f(0) = m 3;
m(m 3) 0; 0 m 3.
Ответ: (0; 3).
Замечание: Эту задачу можно решить и используя теорему Виста (
-
При каких kодин из корней уравнения (k2 2)x2 + (k2 + k 1)xk3 + k2 = 0 меньше k, а другой больше k?
Решение: А = k2 2;
f(k) = (k2 2)k2+ (k2+ k 1)kk3 + k2 =
= (k2 2) ((k2 2)k2+ (k2+ k 1)k k3 + k2) 0;

1 k
Ответ: (
У
 тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий:
тверждение 2. Для того, чтобы отрезок [N; P] лежал в интервале (х1; х2), необходимо и достаточно выполнение условий:А
 f(N) 0;
f(N) 0;А f(Р) 0.
-
При каких mкорни уравнения (m 1)x2 2(m + 2)x + 3m = 0 удовлетворяют условию х1 2, х2 4?
Р


 ешение:
ешение: