Файл: Александры Анатольевны.doc

Решение: y = (x– (5 + a))² + 3 – a; х₀ = 5 + а; y₀ = 3 – a.

5 + а  0, а  –5, –5  а  3.

3 – a 0; а  3;

Целые значения а: –4; –3; –2; –1; 0; 1; 2.

Ответ: 7.
Изучая график квадратного трехчлена, рассматриваем следующие задачи:

12. 
    При каких значениях а парабола y = 9аx²– 12х – 2 имеет с осью 0х две общие точки?
    

Решение: Парабола имеет с осью 0х две общие точки, если дискриминант соответствующего квадратного трехчлена положителен

D₁ = 36 + 9a2 = 36 + 18a;

9а  0, а  0, а  0,

36 + 18a 0; 18a 36; а  2.

Ответ: (–; 0) U (0; 2).

12. 
    При каких m парабола y = mx²– 4mх + 35 касается оси абсцисс?
    

Решение: Парабола касается оси абсцисс, если дискриминант равен 0

D₁ = (2m)²– m35 = 4m²– 35m = 4m (m– );

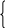
m 0, m 0,

4m(m– ) = 0; m = 0; m = .

m =

Ответ: .

Замечание. При решении таких задач следует всякий раз акцентировать внимание на том факте, что значение первого коэффициента не должно обращаться в ноль.

---

12. 
    Найдите значения а и b, при которых точка (1; 1) является вершиной параболы y = аx²+ bх + 8.
    

Решение: Если точка (х₀; y₀) – вершина параболы, то х₀ = – ; y₀ = y(x₀).

– = 1, b = – 2a, b = – 14,

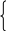
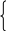a 1² + b1 + 8 = 0; a – 2a + 8 = 1; а = 7.

Ответ: а = 7; b = –14.
Очень содержательными, по-настоящему развивающими исследователь-ские навыки являются задачи типа:

12. 
    Известно, что парабола y = аx²+ bх + с не пересекает ось 0х и a + b + c 0. Определить знаки а и с.
    

Прежде, чем записать решение задачи, рассмотрим утверждения:

1. 
   Если парабола не пересекает ось 0х, то она полностью лежит или над осью, или под осью, то есть при всех х принимает значения одного знака.
   
2. 
   Значение функции при х = 0 равно ее свободному члену, т.е. y(0) = c.
   
3. 
   Значение функции при х = 1 равно сумме коэффициентов y(1) = a + b + c.
   

Решение:

1. 
   y(1) = a + b + c. Так как a + b + c 0, то y(1)  0.
   
2. 
   Функция принимает значения одного знака, следовательноy 0 при всех х, т. е. парабола лежит под осью 0х, таким образом а  0,y(0)  0, с  0.
   

Ответ: а  0; с  0.

12. 
    Квадратный трехчлен аx²+ bх + с не имеет корней, а его коэффициенты связаны условием ab + c 0. Определить знак числа с.
    

Решение:

1. 
   D 0, следовательно y 0 или y 0 для всех х.
   
2. 
   y() = ab + c. Так как ab + c 0, то y()  0, таким образом y 0 для всех х.
   
3. 
   с = y(0); y(0)  0, значит с  0.
   

---

Ответ: с  0.

12. 
    Известно, что квадратное уравнение аx²+ bх + с = 0 не имеет корней и a + cb. Определить знак с.
    

Решение: совпадает с решением задачи 76.

Ответ: с  0.
Пока девятиклассники не научились решать квадратные неравенства, им предлагаются задачи простые по технике решения. Важно, чтобы ученики могли грамотно проанализировать условие и вопрос задачи и правильно составить соответствующую систему.


Квадратные неравенства.
Решение квадратных неравенств с параметрами – один из наиболее сложных вопросов 9 класса. Задачи очень разнообразны по формулировкам и порой достаточно трудоемки, объемны по записи решения, поэтому уже на первых уроках изучения темы "Решение неравенств второй степени с одной переменной" ученики составляют в тетради таблицу, которой активно пользуются сначала при решении числовых неравенств, а потом и неравенств с параметрами.

Изучив графический способ решения квадратных неравенств и рассмотрев примеры всех возможных типов, девятиклассники делают вывод, что возможны шесть случаев положения параболы относительно оси 0х. Факторы, влияющие на положение параболы – знак первого коэффициента и знак дискриминанта. Исследуем решение всех случаев.

Р

ешение квадратных неравенств f (x) ^ 0

f(x) = Ax² + Bx + C, где А, В, С – некоторые числа или выражения,

зависящие только от параметра, причем А  0, х₁ , х₂ – нули функции.

A, D	Эскиз графика	f(x)  0	f(x)  0	f(x)  0	f(x)  0
A 0 D 0		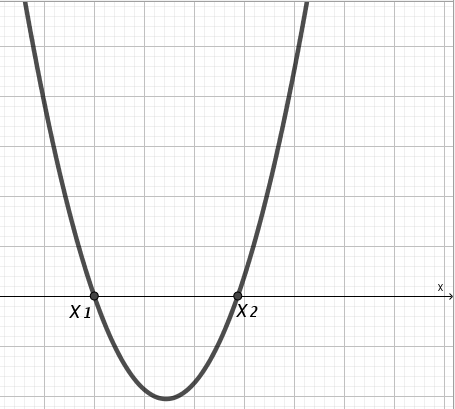(–;х1)U(х2;+)	(–;х1]U[х2;+)	(х1; х2)	[х1; х2]
A 0 D = 0		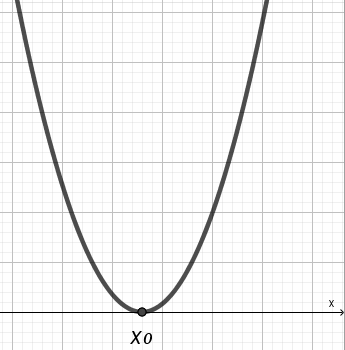(–;х0)U(х0;+)	(–; +)	решений нет	х0
A 0 D 0		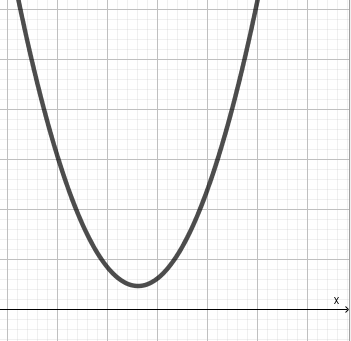R знак значений функции совпа-дает со знаком а	R	решений нет	решений нет
A 0 D 0		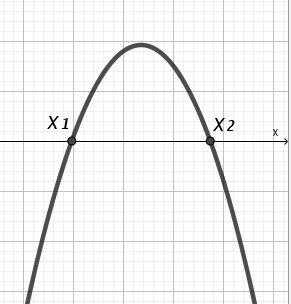(х1; х2)	[х1; х2]	(–;х1)U(х2;+)	(–;х1]U[х2;+)
A 0 D = 0		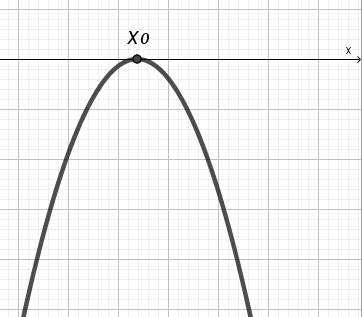решений нет	х0	(–;х0)U(х0;+)	R
A  0 D  0		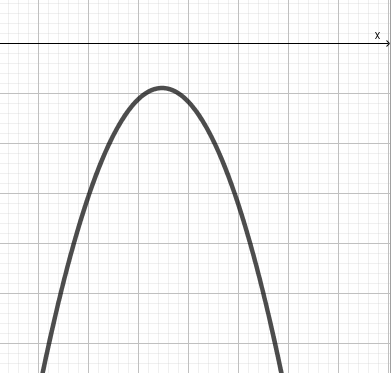решений нет	решений нет	R знак значений функции совпа-дает со знаком а	R

---

В первую очередь ученикам предлагаются неравенства, которые должны выполняться или не выполняться при всех действительных значениях х.

12. 
    При каких значениях а неравенство x² (а + 2)х + 8а + 1  0 выполняется для всех действительных значений х?
    

Р ешение: Неравенство выполняется для всех х, если имеет решение система А  0;

D 0.

1. 
   А = 1; 1  0.
   
2. 
   D = (а + 2)² + 4(8a+1) = а² + 4а + 4  32а  4 = а² 28а = а(а  28).
   
3. 
   а
   а
   (а  28) 0; +  +
   

0  а  28. 0 28

Ответ: (0; 28).

12. 
    При каких значениях b квадратное неравенство (4 b)x² + 2(b+ 2) х  1  0 не имеет решений?
    

При разборе условия задачи ставим акцент на слове "квадратное". Обращаемся к таблице, находим в ней соответствующий случай. Выясняем, что имеется два случая: 1) А  0, D =0;2) А  0, D < 0, которые можно объединить.

Р ешение: Неравенство не имеет решений, если имеет решение система А  0,

D 0.

1. 
   А = 4 b².
   
2. 
   D
   b
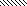
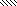   ₁ = (b + 2)² (4  b²) (1) = b² + 4b + 4  b² = 4b + 8.
   
3. 
   4  b² 0, b² 4  0, (b  2)(b + 2)  0, 2 2
   

---

4
b
b + 8  0; 4b 8; b 2.

b2. 2

Ответ: (; 2).

Перед тем, как рассматривать следующую группу задач, полезно обсудить с учениками упражнение:

 При каких значениях а уравнение ах² х + 3 = 0 имеет единственное решение?

Вспомнить, что при изменении параметра могут измениться и важнейшие характеристики уравнения.

12. 
    Найти все значения r, при которых неравенство (r² 1)х² + 2(r 1)x + 2  0 является верным при всех х R.
    

При обсуждении выражения, стоящего в левой части, говорим, что при некоторых значениях rнеравенство будет линейным.

Решение:

1. 
   r² 1 = 0 при r = 1.
   

а) если r = 1, то 4x + 2  0, x0,5, не удовлетворяет условию х R.

б) если r = 1, то 0x2, х R.

2. 
   r² 1  0.
   

Н еравенство выполняется для всех х, если имеет решение система А  0,

D 0.

А = r² 1;

D₁ = (r  1)² 2(r² 1) = (r  1)(r  1 2(r + 1)) = (r  1)( r  3)

r 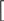² 1  0, (r  1)(r + 1)  0, r 3,

 (r  1)(r + 3)  0; (r  1)(r + 3)  0; r  1.

С учетом п. 1 (б) r 3;

r 1.

Ответ: (; 3) U[1;+

---