ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 288
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(а) (б)


 Т р
Т р
 6 •
6 •Т2 п 3 5 ж



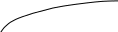 Т(В) р(А)
Т(В) р(А)ж+п ж+п

 Т1 4 р(В) Т(А) 2 ж •1 п
Т1 4 р(В) Т(А) 2 ж •1 п • •
• • А К Мольные доли L В А Мольные доли В
компонента В компонента В
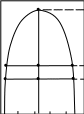
Рис. 2.11. Диаграммы состояния двухкомпонентной системы либо при
р=const (а), либо при Т = const (б): п – пар, ж – жидкость;
2 и 5 – кривые жидкости (кипения), 3 и 4 – кривые пара (конденсации)
Составы жидких и паровых фаз рассматриваемых систем подчиняются первому закону Коновалова: пар содержит больше того компонента, добавление которого к раствору понижает температуру его кипения при данном давлении или повышает общее давление пара при данной температуре (т.к. пар обогащается более летучим компонентом).
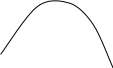
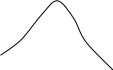
Некоторые вещества при строго определенных соотношениях компонентов могут образовывать азеотропные растворы – т.е. такие растворы, при испарении которых получается пар такого же состава, что и состав раствора. Другими словами, азеотропные растворы перегоняются без изменения состава. На кривых диаграмм состояния в точках, отвечающих составам азеотропных растворов, имеются экстремумы (рис.2.12). При этом изменение внешнего давления приводит не только к изменению температуры кипения азеотропного раствора, но и его состава. Это указывает на то, что азеотропный состав компонентов не соответствует составу химического соединения. Азеотропные растворы называют нераздельнокипящими. О них можно сказать, что они испаряются как индивидуальные чистые вещества. Системы, содержащие составы азеотропных растворов, подчиняются второму закону Коновалова: точки максимума или минимума на кривых общего давления насыщенного пара (и соответственно точки минимума или максимума на кривых температур кипения) отвечают растворам, состав которых одинаков с составом их насыщенного пара.
Жидкость
Пар
А Состав В
мольные доли
Пар
Жидкость
А Состав В
мольные доли


 (а) (б)
(а) (б) 






Рис. 2.12. Диаграммы состояния системы (А+В), образующей азеотропные
смеси, при постоянной температуре (а) и при постоянном
давлении (б)
Помимо законов Коновалова в основе теории рассматриваемых систем лежат законы Вревского. Первый закон: при фиксированном составе жидкой фазы равновесная с ней газовая (паровая) фаза обогащается с увеличением температуры (давления) тем компонентом, для которого больше мольная теплота испарения, т.е. менее летучим компонентом. Второй закон Вревского: при повышении температуры (давления) в азеотропной смеси с максимумом температуры кипения увеличивается содержание компонента, обладающего меньшей мольной теплотой испарения; в азеотропной смеси с минимумом температуры кипения с повышением температуры возрастает относительное содержание компонента с большей мольной теплотой испарения.
На рассмотренных законах основано разделение жидких растворов с летучими компонентами. Соотношение между количествами жидкости и пара в равновесии определяют по правилу рычага: отрезки горизонтальной прямой, соединяющей паровую и жидкую фазу, образуемые определенной точкой (точкой определенного состава) этой прямой, обратно пропорциональны числам молей каждой из фаз. Например, для некоторой точки М в гетерогенной области диаграммы состояния рис. 2.13.(а) имеем:
n ж / n п = а
/ в.
(б)



(а)


 Т
Т
 п
п  •М
•М
а в
 ж
жА Мольные доли В
компонента В
Т n



 Тх
Тх


 Т2
Т2


 Т1
Т1


 Т0
Т0Д ●
 ж
ж А
Мольные доли компонента В
Рис. 2.13 . Диаграммы остояния системы (А-В) при р=const к вопросу
определения состава жидких и парообразных фаз и разделения
растворов на фракции
Дистилляция или дробная перегонка - это разделение жидких растворов, основанное на различии составов жидкости и пара. Дистилляция осуществляется путем частичного испарения и последующей конденсации пара. Отогнанная фракция (дистиллят) обогащена более летучим компонентом. Оставшаяся жидкость называется кубовым остатком, она обогащена менее летучим компонентом.
Например, если нагреть исходный раствор состава Xo (рис. 2.13(б) точка Д) до температуры кипения Т0,, то при этом образуется первый пузырек пара состава
Для повышения степени разделения растворов применяют перегонку с дефлегмацией. Пар из перегонного куба поступает в дефлегматор, где он частично конденсируется. Из пара преимущественно конденсируется высококипящий компонент, и флегма сливается обратно в куб.
110
100 b a
Пар
d
с
90 Жидкость
f е
g
80
0 0,2 0,4 0,6 0,8 1,0
Бензол Толуол
Мольная доля толуола












Рис. 2.14. Точки кипения смесей бензол – толуол; состав жидкости и пара (жидкость кипит при температурах, изображаемых нижней кривой)
ЛЕКЦИЯ 10
В качестве примера, на рис. 2.14 показано, что раствор с мольной долей толуола 0,75 и мольной долей бензола 0,25 кипит при 100 оС и 1 атм (точка а). Его равновесный пар богаче более летучим компонентом (бензолом) и имеет состав b. Этот пар можно сконденсировать, понижая температуру по линии bc. Если испарить небольшую часть полученной жидкости, то первая порция образовавшегося пара будет иметь состав, соответствующий точке d. Этот процесс испарения и конденсации можно повторять многократно, и в результате будет получена фракция с высоким содержанием бензола.
Каждое испарение и каждая конденсация, представленные ломаной линией abcde на рис 2.14, соответствуют идеальному процессу, в ходе которого конденсируются и вновь испаряются только малые количества вещества. На практике удобнее осуществлять разделение в перегонной колонне, например в колонне колпачкового типа (рис. 2.15). Такой процесс называется ректификацией.
8
1
2
↓
3 4
5
6
7
8
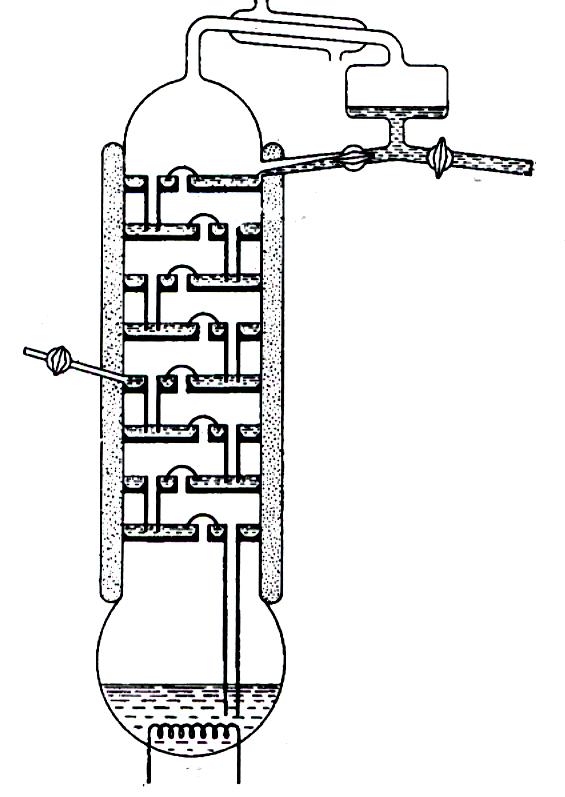

Рис. 2.15. Колпачковая ректификационная колонна: 1 – холодильник;
2 – колпачок; 3 – флегма; 4 – дистиллят; 5 – пар; 6 – жидкость;
7 – ввод; 8 - нагреватель
Каждый слой жидкости на тарелках колонны эквивалентен кипящей жидкости в перегонной колбе, жидкость на тарелке, расположенной выше, эквивалентна конденсату. Пар проходит вверх через колпачки, частично конденсируется в жидкости и смешивается с ней. Часть полученного раствора испаряется и затем конденсируется в вышележащем слое, в то время как часть жидкости стекает по трубке на нижележащую тарелку. В результате из верхней части колонны выходит непрерывный поток пара, полученного последовательным испарением, а в перегонный куб возвращается непрерывный поток жидкости, которая получена последовательной конденсацией. Для компенсации убыли вещества в перегонной колонне в нее вводится свежий раствор, обычно в середине колонны. Колонна должна быть хорошо изолирована или снабжена рубашкой с контролируемым обогревом, чтобы предотвратить слишком интенсивную конденсацию на стенках. Вся система достигает стационарного состояния, при котором состав раствора на каждой тарелке остается неизменным, пока сохраняется постоянным состав жидкости в перегонном кубе.
Перегонная колонна может быть заполнена инертным материалом (насадкой), который обеспечивает эффективный контакт между жидкостью и паром и занимает лишь небольшой объем, чтобы оставалось достаточно свободного пространства для больших количеств пара. В качестве насадок, действующих с различной эффективностью, применяют стеклянные кольца, сетчатые спирали и некоторые другие типы материалов.
Эффективность колонны выражается эквивалентным числом теоретических тарелок. Число теоретических тарелок в колонне равно числу последовательных бесконечно малых равновесий жидкость-пар, обеспечивающих разделение, которое действительно достигается в колонне. Число теоретических тарелок до некоторой степени зависит от коэффициента дефлегмации, т.е. от отношения скорости возврата жидкости в головку колонны к скорости отбора дистиллята. Число теоретических тарелок перегонной колонны в рабочих условиях можно найти, сосчитав, сколько раз нужно провести равновесное испарение, чтобы получить разделение, которое действительно достигается в колонне. Предположим, что при перегонке смеси бензола и толуола в некоторой ректификационной колонне найдено, что дистиллят состава g получается в том случае, когда состав жидкости в кубе соответствует точке a (рис.2.14). Такая перегонка эквивалентна трем простым процессам испарения и конденсации, которые изображены ступенчатыми линиями abc, cde и efg. Поскольку перегонный куб сам соответствует одной теоретической тарелке, колонна имеет две теоретические тарелки.
Если два компонента образуют азеотропную смесь, то такую систему можно разделить на один из чистых компонентов и азеотропную смесь. В системах с минимумом температуры кипения в парообразную фазу будет уходить азеотропная смесь, а оставшаяся жидкость будет представлять собой тот чистый компонент, который преобладал в исходной смеси. В системах с максимумом в составе пара будет преобладать тот компонент, которым была богаче исходная жидкость, а оставшаяся жидкость будет стремиться к составу азеотропной смеси.
2.3.4. Равновесие газ - жидкий раствор
Растворимость газа в жидкости часто выражают коэффициентом растворимости , который численно равен объему газа в м3, растворенному в 1 м3 растворителя при данной температуре и парциальном давлении газа 1 атм: = Vг / Vо . Коэффициент растворимости зависит от температуры. Растворение газа в жидкости может происходить в результате проявления между частицами газа и жидкости сил Ван-дер-Ваальса, водородных связей, химического взаимодействия, а также вследствие диссоциации молекул газа в растворителе.
Для разбавленных растворов справедлив закон Генри: мольная доля газа(Хг) в растворе пропорциональна парциальному давлению газа над раствором (рг), находящимся в равновесии с газом:
Хг = рг / kг, (2.17)
где kг – константа Генри данного газа, которая измеряется в Па, зависит от температуры и так же, как и коэффициент растворимости, определяет содержание газа в растворе.
Растворимость газов в воде обычно уменьшается при добавлении других растворимых веществ, в частности электролитов. Такое явление называется высаливанием. Высаливающее действие ионов повышается с ростом их заряда и уменьшением радиуса. Это объясняется более сильной сольватацией ионов молекулами растворителя, нежели молекул газа. В результате значительная часть молекул растворителя выключается из участия в растворении газа. Примером может служить выделение пузырьков газа при добавлении щепотки соли к газированной воде.
Растворимость газов в жидкостях, как правило, падает при увеличении температуры, потому что в процессах растворения теплота обычно выделяется. Однако имеются и исключения, например, в случае жидкого аммиака и некоторых органических жидкостей. Если представить равновесие между газом и раствором как равновесие между раствором и насыщенным паром растворенного вещества, которое зависит от Т, то в соответствии с уравнением Клаузиуса - Клапейрона получим
р = (RT2/p) dp/dT ,
где p - тепловой эффект растворения газа. Видно, что чем больше Т, тем больше давление газа, то есть тем меньше его растворимость. Поэтому прежде чем растворять газ, например, в воде его следует охладить.
2.3.5. Равновесие жидкость - жидкость
Существуют растворы с неограниченной или ограниченной растворимостью, а также системы с полной нерастворимостью жидкостей друг в друге. При ограниченной растворимости взаимная растворимость, как правило, возрастает с увеличением температуры (системы с верхней критической температурой растворения). В некоторых случаях при этом взаимная растворимость уменьшается (системы с нижней критической температурой растворения). Критической называют температуру (Тк), при которой либо составы равновесных жидких фаз одинаковы, либо ограниченная растворимость жидкостей переходит в неограниченную.
На рис. 2.16 в качестве примера приведена диаграмма состояния системы анилин – вода, компоненты которой обладают ограниченной взаимной растворимостью. Кривая АВ показывает зависимость состава водного слоя от температуры, кривая ВС – зависимость состава анилинового слоя от температуры. С ростом температуры увеличивается взаимная растворимость анилина в воде и воды в анилине. Когда оба слоя становятся одинаковыми по составу, кривые сливаются в точке В (при 440,6 К). Температура, выше которой обе жидкости смешиваются в любых соотношениях, называется верхней критической температурой растворимости. Конноды а1а2 и b1b2 cоединяют фигуративные точки равновесных (сопряженных) слоев. За пределами кривой АВС находится область однофазных систем, внутри кривой АВС – область расслаивания. Например, система обозначенная фигуративной точкой ао, разделяется на два слоя, составы которых отвечают точкам а1 и а2 (Ф=2; С=1). Характерной особенностью таких систем является то, что при неизменной температуре при изменяющемся составе всей системы состав отдельных фаз не меняется, а изменяется только их количественное соотношение. Если кривая, ограничивающая область расслаивания, проходит через минимум, что наблюдается, например, у системы вода-триэтиламин, то температура Тк называется нижней критической температурой растворимости.
 Т,К Тк
Т,К Тк440,6
440 В
400
а1 а0 а2Та
b1 b0 b2
360 Тb
320 А D C
0 0,2 0,4 0,6 0,8 1
H2O C6H5NH2
Массовые доли C6H5NH2
Рис. 2.16. Диаграмма состояния системы вода – анилин
Критическую точку растворимости на кривой расслаивания определяют, пользуясь правилом прямолинейного диаметра Алексеева, согласно которому середины коннод, соединяющих фигуративные точки сопряженных растворов, лежат на прямой линии, проходящей через верхнюю или нижнюю критическую точку растворимости.
Многие двухкомпонентные системы имеют сложные диаграммы состояния, которые представляют собой комбинацию из нескольких простых диаграмм. В некоторых системах критические температуры растворения не достигаются, т.к. при повышении температуры одна из жидкостей превращается в пар, а при понижении температуры одна из жидкостей кристаллизуется.
Так, если две жидкости ограниченно растворимы друг в друге, то диаграмма кипения системы имеет следующий вид.






 Т Р
Т Р
 1 1
1 1
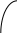
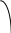
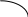

 5 6 2 5 О
5 6 2 5 О


 2 3 6
2 3 6О 4 3
4

 А X1 X2 В А В
А X1 X2 В А ВРис. 2.17. Диаграммы состояний двух ограничено растворимых друг в друге жидкостей
На данной диаграмме можно выделить шесть областей: 1 - область пара; 2 - область первого раствора; 3 - область второго раствора; 4 - область двух растворов; 5 - область пара и первого раствора; 6 - область пара и второго раствора. В первых трех областях системы гомогенны, и число степеней свободы равно 2, а в последних трех областях они гетерогенны, и число степеней свободы равно 1.
Гетероазеотропом называется гетерогенная система (точка О), состоящая из двух ограниченно смешивающихся жидкостей составов X1 и X2 , а также пара с составом, промежуточным между составами жидких фаз. Гетероазеотропная смесь имеет наинизшую температуру кипения по сравнению с температурами кипения смесей любого другого состава. Поэтому ее нельзя разделить с помощью перегонки. Способность ограниченно смешивающихся жидкостей образовывать гетероазиотропы используется для разделения компонентов, образующих азеотропные смеси. Например, имеются две жидкости Ж1 и Ж2, образующие азеотропную смесь. Ее нельзя разделить с помощью перегонки. Если добавить к азеотропной смеси третью жидкость Ж3, которая с Ж1 образует гетероазеотроп, кипящий при более низкой температуре, чем азеотропная смесь, то гетероазеотроп перейдет в дистиллят, а Ж2 останется в кубовом остатке.
2.4. ФАЗОВЫЕ РАВНОВЕСИЯ В ТРЕХКОМПОНЕНТНЫХ СИСТЕМАХ
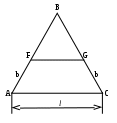
Для трехкомпонентных систем С=3+2 - Ф= 5-Ф. Число фаз в равновесии не может быть больше 5 при инвариантности системы. Максимальное число степеней свободы равно 4: давление, температура, концентрации двух компонентов. Следовательно, диаграмма состояния должна быть четырехмерной. При постоянном давлении диаграмма представляет собой трехгранную призму, основанием которой служит равносторонний треугольник составов (треугольник концентраций), а по высоте откладывается температура. Изучение равновесий еще более упрощается, если рассматривать сечения призмы, то есть рассматривать системы при постоянных давлении и температуре. В этом случае диаграмма состояния представляет собой двумерный равносторонний треугольник (треугольник концентраций), вершины которого соответствуют чистым компонентам, например, А, В, С. Фигуративные точки, лежащие на сторонах треугольника , соответствуют составам двухкомпонентных систем, а точки, лежащие внутри треугольника, - составам трехкомпонентных систем. Например, если состав системы соответствует точке 1 ( рис. 2.18а), то в системе присутствуют только компоненты В и С, а если состав соответствует точке 2, то в системе имеются все три компонента.
Для определения содержания каждого компонента в системе используют два метода, основанные на свойствах равносторонних треугольников. Метод Гиббса лучше использовать в том случае, если нужно определить состав в точке, уже нанесенной на диаграмму (например, в указанной точке 2). Для этого надо опустить перпендикуляры из точки 2 на стороны треугольника. При этом сумма длин перпендикуляров равна высоте равностороннего треугольника (h), которая принимается за единицу. Доля данного компонента в системе вычисляется отношением к длине высоты длины перпендикуляра, опущенного на противолежащую сторону от вершины треугольника, соответствующей данному компоненту. Так, для рассматриваемой точки 2 выполняются следующие равенства:
a + b + c = h;
Х(A) = a / h; Х(B) = b / h; Х(C) = c / h.
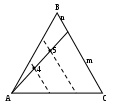
Второй метод (метод Розебума) позволяет определять состав трехкомпонентной системы, представленный какой-либо точкой внутри треугольника концентраций, по трем отрезкам на одной из сторон треугольника. Для этого через данную точку (например, точку 3 рис.2.18 б) надо провести прямые, параллельные двум сторонам треугольника (KL и МN). При этом третья сторона треугольника разбивается на три отрезка, по длинам которых судят о составе трехкомпонентной системы в данной точке (АМ, ML, LC или соответственно с, b, a). Длину стороны равностороннего треугольника принимают за единицу (l=1). Доля каждого компонента оказывается пропорциональной длинам отрезков (равным между собой), прилегающих к вершинам состава других компонентов, и отсекаемых прямой, параллельной стороне треугольника, которая находится напротив вершины состава данного компонента. Например, доля компонента А пропорциональна отрезкам КВ и LC (т.е. длине отрезка а): Х(А)=а/l. Аналогично, Х(В)=b/l; Х(С)=с/l. Метод Розебума предпочтителен в том случае, если на диаграмму надо нанести точку, отражающую состав системы. Например, для построения точки, отражающей состав системы 0,5 А, 0,3 В и 0,2 С, надо по четырем уравнениям (a + b + c = l; a/l = 0,5; b/l = 0,3; c/l= 0,2) найти значения a, b, c и l. Далее на стороне треугольникаl отложить отрезки a, b и c и через две полученные точки провести прямые, параллельные соответствующим сторонам треугольника. Точка их пересечения будет искомой точкой указанного состава. Другими словами, надо выполнить действия, показанные на рис. 2.18 б, но в обратном порядке.
В
а
с
2 h • 1
b
A C
B
c
N
a
K
3
b b
c b L а
A M C
l




а б
в г
Рис.2.18. Равносторонние треугольники концентраций диаграмм
состояний трехкомпонентных систем А+В+С при
постоянных р и Т (пояснения в тексте)
Из подобия соответствующих треугольников, показанных на рис. 2.18 в, следует, что все точки, которые лежат на прямой, проходящей через вершину треугольника концентраций, отражают составы с постоянным соотношением концентраций двух других компонентов. Например, в точках 4 и 5 соотношения Х(В)/Х(С) одинаковы и равны отношению отрезков m и n.
Точки, лежащие на прямой, параллельной одной из сторон треугольника, отражают составы системы с постоянным содержанием компонента, противолежащего данной стороне. Так, на прямой FG (рис.2.18 г), параллельной АС, лежат точки с одинаковым содержанием компонента В, равным b / l .
ЛЕКЦИЯ 11 2.4.1. Диаграмма состояния системы: вода и две соли
с одноименным ионом
Допустим, что рассматриваемая диаграмма относится к системе, в которой не образуется двойных солей и кристаллогидратов, а присутствуют только соли А и В и вода (рис. 2.19). Если точка m характеризует состав двухкомпонентной системы, а именно насыщенного водного раствора соли А, а точка n – состав насыщенного водного раствора соли В, то точки на кривой mB выражают составы трехкомпонентной системы, насыщенной по отношению к соли А, а точки на кривой nA выражают составы растворов, насыщенных по отношению к соли В. Из диаграммы следует, что с ростом относительного содержания одной соли, растворимость другой соли уменьшается. Точка k выражает состав раствора, насыщенного сразу по обеим солям, и называется эвтоникой.


Н2О
1
m n
k
2 3
4
A B

Рис.2.19. Диаграмма растворимости в воде двух солей (А и В) с одноименным ионом. Изотермическая проекция на треугольник концентраций
На диаграмме показаны четыре фазовые области: 1 - ненасыщенного раствора солей А и В в воде (система гомогенная; число степеней свободы равно 2); 2 - раствора солей А и В в воде, насыщенного по отношению к соли А и содержащего ее кристаллы; 3 - раствора солей А и В, насыщенного по отношению к соли В и содержащего ее кристаллы; 4 -раствора, насыщенного по отношению к обеим солям и содержащего их кристаллы.
Рассмотрим далее, как протекает процесс испарения воды из исходного раствора, состав которого характеризуется точкой R на диаграмме рис.2.20. Очевидно, что при этом состав системы будет изменяться вдоль прямой, проходящей через точку R и вершину Н2О, т.к. при этом соотношение концентраций солей в системе не будет изменяться.
H2O
R • m
n p • y
k
• z
• w
s•
B H Ф А





Рис.2.20. Диаграмма растворимости в воде двух солей (А и В) с одноименным ионом. Изотермическая проекция на треугольник концентраций. Процесс выпаривания раствора состава R
Такая прямая называется лучом испарения. Система будет оставаться гомогенной до достижения точки y, в которой она окажется насыщенной по отношению к соли А. В этой точке выпадут в осадок первые кристаллики соли А. Число степеней свободы в точке y станет равным единице (С = К + n – Ф = 3 + 0 – 2 = 1). Следовательно, если далее уменьшать содержание воды в системе, то состав раствора должен изменяться в соответствии с кривой mk.
В точке z в равновесии будут находиться кристаллы соли А и раствор, состав которого можно определить, проведя прямую через вершину А и точкуz до пересечения с кривой mk. При этом состав раствора характеризуется точкой р, а по правилу рычага можно вычислить соотношение масс кристаллов А и раствора:
m(A) / m(раствора) = zp / zA.
При продолжении испарения воды в точке w раствор становится насыщенным по отношению к соли В, и начнется ее кристаллизация наряду с продолжающейся кристаллизацией соли А. Число степеней степеней свободы в системе становится равным нулю (С = К + n – Ф = 3 + 0 – 3 = 0). Это значит, что до полного исчезновения воды состав раствора не изменяется и соответствует составу эвтоники (точка k). Далее в точке s в равновесии будет находиться три фазы. Для определения их количеств следует провести конноду через эту точку и эвтонику. Коннода пересечет АВ в точке Ф и по правилу рычага выполнятся следующие уравнения:
m(А + В) / m( раствора) = sk / sФ;
m(А) / m(В) = ФВ / ФА.
При полном испарении воды система окажется двухкомпонентной, и ее состав будет отражать точка Н.
Выпаривание раствора используется для очистки веществ (например, соли А) в тех случаях, когда растворимость веществ мало изменяется с температурой. Другим методом очистки веществ является перекристаллизация. Растворимость большинства твердых тел с повышением температуры увеличивается. Это происходит потому, что в таких случаях процессы растворения являются эндотермическими. Перекристаллизация основана на зависимости растворимости веществ от температуры (если она существенна). Тогда при остывании горячего насыщенного раствора соли, загрязненной посторонними примесями, значительная ее часть выделится в осадок, а загрязняющие примеси останутся в растворе, так как последний не будет насыщенным по отношению к этим примесям. В реальной системе осадок все же в той или иной степени будет загрязнен примесями, так как это приводит к повышению энтропии системы, а следовательно к понижению химического потенциала. Повышения степени очистки можно добиться путем многократного повторения перекристаллизации в новых порциях растворителя.
2.4.2. Диаграмма состояния трех жидкостей
с ограниченной растворимостью
Диаграммы растворимости таких систем отличаются разнообразием. Наиболее часто встречаются системы, в которых две жидкости А и В обладают ограниченной растворимостью друг в друге, а третья жидкость С неограниченно смешивается с первыми двумя. Проекция диаграммы состояния такой системы показана на рис. 2.21. При введении жидкости С в смесь А и В взаимная растворимость А и В увеличивается, и при некотором содержании С она переходит в неограниченную, то есть система становится гомогенной.
На диаграмме видны две области, разделенные кривой расслоения DE. Любая точка внутри области 1 соответствует гомогенной трехкомпонентной системе. Точки, расположенные внутри области расслоения 2, соответствуют двухфазной системе. Например, при смешивании трех жидкостей в соотношении, определяемом точкой 3, происходит расслоение системы на два раствора, каждый из которых содержит все три жидких компонента. Составы этих равновесных растворов характеризуются точками m и n. Коннода, соединяющая эти точки, не параллельна АВ, т.к. растворимость С в компонентах А и В неодинакова. Существует приближенное правилo Тарасенкова, согласно которому все конноды, соединяющие точки равновесных растворов, пересекаются в одной точке F на продолжении стороны треугольника. Касательная к кривой расслоения, проведенная из точки F, даст точку К, называемую критической точкой растворения, в которой составы равновесных фаз становятся одинаковыми, и система переходит в гомогенную.
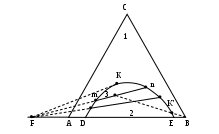
Рис.2.21. Диаграмма состояния трехкомпонентной жидкой системы в виде изотермической проекции при некоторой температуре Т
При дальнейшем добавлении к системе одной из жидкостей (А или В), составы равновесных растворов будут изменяться, и при некотором количестве добавленной жидкости система снова окажется гомогенной. Например, при добавлении жидкости В расслоение исчезнет в точке К'.
Повышение температуры, как правило, приводит к увеличению взаимной растворимости жидкостей. Гетерогенная область на диаграмме сужается, и при критической температуре система становится гомогенной при любом составе. Некоторые трехкомпонентные системы характеризуются двумя (вода - фенол - анилин), а также тремя областями расслоения (вода - нитробензол - гексан).
2.4.3. Экстракция
Экстракция – это метод очистки или разделения веществ, основанный на их различной растворимости в двух несмешивающихся жидкостях. Он широко используется для разделения смесей, а также для концентрирования веществ в процессах синтеза. В частности, метод применяется для очистки воды от загрязнений.
Например, если к системе двух взаимно нерастворимых жидкостей ЖI и ЖII добавить вещество А, способное в них растворяться, то оно каким-то образом распределится между жидкостями. В состоянии равновесия химические потенциалы вещества А в жидких фазах будут равны:
(А)1 = (А)II .
Или, учитывая активности растворенного вещества А в несмешивающихся растворителях а(А)I и а(А)II,
(А)I + RTln a(А)I = (А)II + RTln a(А)II,
где (А)I и (А)II – стандартные химические потенциалы вещества А в соответствующих растворителях. После преобразования последнего уравнения следует равенство:
ln [a(A)I / a(A)II ] = ( (А)II - (А)I) / RT.
Видно, что правая часть уравнения представляет собой постоянную величину, которую можно представить в виде логарифма – lnKо. Тогда:
а(А)I / a(А)II = K.
Последнее уравнение выражает закон распределения Нернста - Шилова: третий компонент, добавляемый к системе, состоящей из двух взаимно нерастворимых или ограниченно растворимых жидкостей, распределяется между обеими жидкостями в определенном и постоянном при данной температуре отношении. Величина К называется термодинамической константой распределения. Если берется отношение не активностей, а концентраций, то константа называется коэффициентом распределения:
К= с(А)I /с(А)II .
Очевидно, что для разбавленных растворов: а = с и К = Ко.
Если в одном из растворителей, например ЖII, происходит преимущественное концентрирование молекул А, то ее можно применить в качестве экстрагента для извлечения вещества А из раствора на основе первой жидкости. При этом следует учитывать образование ассоциатов из молекул А в растворителях. Например, если М2 - средняя молярная масса вещества в экстрагенте; М1 - средняя молярная масса вещества в очищаемом растворе, то закон распределения будет выглядеть следующим образом:
с1n / с2 = К,
где с1 - концентрация вещества А в очищаемом растворе; с2 - концентрация вещества А в экстрагенте; n = М2 / М1 .
Если распределяющееся вещество А будет диссоциировать в растворителях, то закон распределения примет вид:
с1(1 - ) / с2(1 - ) = К,
где и 2 – степени диссоциации соответственно в очищаемом растворе и в экстрагенте.
Наиболее эффективно проводить экстрагирование последовательно небольшими порциями экстрагента (v). Это позволяет, с одной стороны, повысить степень очистки при одном и том же общем количестве экстрагента. С другой стороны, для достижения требуемой степени очистки, можно израсходовать меньшее количество экстрагента.
Допустим, что в некотором объеме исходного раствора V находится некоторое количество m0 вещества, которое нужно извлечь. Пусть молярная масса вещества в обоих растворителях будет одинакова и процесс проводится небольшими порциями экстрагента объемом v. Тогда после первого экстрагирования в исходном растворе останется m1 вещества, а в экстракт перейдет (m0 - m1) вещества.
В состоянии равновесия выполнится равенство:
К = с1/с2 = (m1 / V ) : [(m0 - m1 ) / v ].
После его преобразования получим:
m1 = m0 [ К V / (v + К V)].
Аналогично рассуждая, можно получить после х экстрагирований:
mх = m0 [ К V / (v + К V)]х .
Видно, что выражение в квадратных скобках меньше единицы, следовательно, m1
Тема 3. Химическая кинетика
3.1. ОСНОВНЫЕ ПОНЯТИЯ
Химическая кинетика – это раздел физической химии, в котором изучаются скорости химических реакций и те промежуточные продукты (интермедиаты), которые образуются в процессах протекания реакций. Скорость химической реакции оценивают по изменению количества реагента или продукта (моль) в единицу времени в единице объема (для гомогенной реакции) или на единице поверхности раздела двух фаз (для гетерогенной реакции): v = ∆c/∆. Скорость реакции растет с увеличением концентрации реагентов вследствие роста вероятности столкновения их частиц в реакционном пространстве. Для реакции
аА + вВ → сС (3.1)
выполнится следующее кинетическое уравнение, если она протекает в одну стадию, т.е. является элементарной:
v = kca(A)cв(B), (3.2)
где k – константа скорости реакции. Показатели степени при молярных концентрациях веществ в кинетических уравнениях чаще всего не совпадают со стехиометрическими коэффициентами уравнений реакции. Их надо определять экспериментально. Кинетические уравнения реакций – это математическое выражение зависимости их скорости от концентраций реагентов, называемое также законом действующих масс.
Реакции, протекающие одновременно как в прямом, так и в обратном направлениях, называются двусторонними или обратимыми. Связь между равновесными концентрациями веществ, участвующих в обратимой химической реакции, выражается константой равновесия (Кс), например:
аА + вВ ⇄ сС ,
 (3.3)
(3.3)Последнее выражение также называется законом действующих масс. Оно строго выводится в термодинамике.
Молекулярность реакции - это число молекул, участвующих в элементарных актах реакции. Молекулярность элементарных химических актов может быть 1, 2, реже 3 (соответственно моно-, би-, тримолекулярные реакции). Вероятность одновременного столкновения и взаимодействия большего числа частиц практически равна нулю. Как уже отмечалось, в случаях сложных реакций показатели степеней концентраций кинетических уравнений не равны соответствующим стехиометрическим коэффициентам. В таких реакциях последние показывают только соотношения количеств веществ в уравнениях реакций (в элементарных реакциях они указывают и на их порядок).
Показатель степени при концентрации реагента в кинетическом уравнении называется порядком реакции по данному реагенту. Сумма порядков реакции по всем реагентам называется порядком реакции. Он может быть равен нулю, принимать целые, дробные и отрицательные значения.
Иногда требуется определить количество вещества (например, А), прореагировавшего к определенному моменту времени τ (Аτ). В таком случае доля Аτ от начального количества вещества Ао называется степенью превращения (α): α = Аτ /Ао или α=(сo-сτ)/сo, где сτ – концентрация Ав момент τ. Время полураспада вещества 0000000000000001/2 - это время, за которое его начальная концентрация уменьшается вдвое.
По первому порядку протекают многие реакции разложения, изомеризации, а также реакции гидролиза в водных растворах, так как концентрация воды в последних практически не изменяется и может быть введена в константу скорости. Односторонние реакции второго порядка - это реакции двух видов: 1) А + В продукты и 2) 2А продукты. В реакциях нулевого порядка скорость реакций не зависит от концентраций реагентов. Основными методами определения порядка реакций являются следующие:
1) Метод подстановки. По экспериментальным данным следует проверить, какое из кинетических уравнений лучше описывает зависимость с=f(). Для этого вычисляют константу скорости реакции по уравнениям различного порядка при разных с. Если для какого-то уравнения значения k примерно постоянны, то это уравнение правильно описывает процесс.
2) Графический метод. Зависимость концентрации от времени для реакций различных порядков может быть выражена прямой линией, если выбрать соответствующую систему координат:
| Порядок реакции | Нулевой | Первый | Второй | Третий |
| Кинетическое уравнение | с = с0 - k | ln c = ln с0 - k, | 1/c = 1/ с0 + k | 1/c2 =1/ с02 + 2k |
Например, разложение ацетальдегида при 500 С протекает по уравнению:
СН3СНО(г) = СН4(г) + СО(г).
Первоначально можно предположить, что это реакция первого порядка. Однако, прямая зависимость получается не в координатах ln p(СН3СНО) - , а в координатах 1/p(СН3СНО) - (в случае реакций в газообразной фазе вместо молярных концентраций можно пользоваться парциальными давлениями реагентов). Это говорит о том, что данная реакция протекает по механизму второго порядка, и в элементарном акте реакции участвуют две молекулы ацетальдегида:
2СН3СНО = 2СН4 + 2СО.
3) По времени полупревращения:
| Порядок реакции | Нулевой | Первый | Второй | Третий |
| 1/2 | с0 | не зависит от начальной концентрации | 1/с0 | 1/с02 |
Представления о порядке реакций уместны для односторонних реакций, которые протекают до полного исчезновения реагентов. Большинство реакций являются двусторонними. Суммарная скорость двустороннего процесса будет равна разности скоростей прямой и обратной реакций:
v = v - v .
В таких системах равновесие возникает тогда, когда скорости прямой и обратной реакций становятся одинаковыми. Это означает, что суммарная скорость обратимой реакции равна нулю:
v = 0; v = v .
Обычно считается, что если константы скоростей обратимой реакции отличаются более чем на два порядка, то реакция протекает практически как односторонняя.
ЛЕКЦИЯ 12 3.2. ЗАВИСИМОСТЬ СКОРОСТИ
ГОМОГЕННЫХ РЕАКЦИЙ ОТ ТЕМПЕРАТУРЫ
Как правило, скорость химических реакций с повышением температуры увеличивается. Голландским химиком Вант-Гоффом экспериментально установлено, что при увеличении температуры на каждые 10 ˚С скорость большинства реакций возрастает в 2÷4 раза. Это правило можно записать следующим образом:
 (3.4)
(3.4)где γ – температурный коэффициент скорости реакции; γ = 2 ÷ 4. Формулу (3.4) можно преобразовать с учетом увеличения температуры на любую величину:
 откуда:
откуда: 
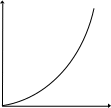
Видно, что при этом возрастает константа скорости. Вид зависимости k от Т, а также lnk от величин 1/Т (Т – абсолютная температура) представлен на рис. 3.1.
Шведский физико-химик С.Аррениус исследовал зависимость константы скорости реакций от температуры и показал, что она выражается эмпирическим уравнением:
k=Ае-Е/RT, (3.5)
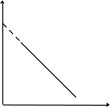
где е – основание натурального логарифма; А – постоянная, характеризующая каждую конкретную реакцию (константа Аррениуса); Е – еще одна постоянная, характерная для каждой реакции; R – газовая постоянная, Т – абсолютная температура в кельвинах. В логарифмической форме уравнение (3.5), называемое уравнением Аррениуса, приобретает вид:
lnk=lnA-E/RT
или (3.6)
lgk=lgA-E/2,3RT.
а б
 k lnk
k lnklnA
tgα= − E/R
α
T, K 1/T, K-1
Рис. 3.1. Зависимости константы скорости реакции k
от температуры Т (а) и lnk от 1/Т (б)
В виде (3.6) уравнение Аррениуса используется наиболее часто. При этом константы А и Е, характеризующие конкретную реакцию, находят графически по экспериментальной прямой, аналогичной прямой рис.3.1 б. Ее пересечение с осью у определяет значение lnA, а тангенс угла наклона равен – E/R. По (3.5) и (3.6) видно, что чем больше значение Е, тем меньше величина k, т.е. тем меньше скорость реакции, а чем больше значение А, тем больше k и скорость реакции. Если для двух значений Т определить константы скорости, то по (3.6) можно вычислить значение Е:
при Т1:

а при Т2:

Вычитая второе равенство из первого, получим:
 ,
,откуда следует:
 (3.7)
(3.7)Уравнение (3.7) дает также удобный способ вычисления константы скорости при некоторой температуре Т2, если известны постоянная Е и константа скорости k1 при температуре Т1.
3.3. КИНЕТИЧЕСКИЕ ТЕОРИИ ХИМИЧЕСКИХ РЕАКЦИЙ
Теория соударений
Для объяснения зависимости скорости химических реакций от концентраций реагентов и температуры была создана на основе кинетической теории газов теория соударений. По этой теории в смеси двух газообразных веществ А и В их молекулы должны столкнуться, чтобы между ними произошла химическая реакция. Было теоретически доказано, что частота столкновений Z пропорциональна произведению концентраций А и В:
Z
Если бы каждое соударение приводило к химическому превращению, то скорость реакции была бы равна частоте соударений. Теоретические вычисления этой частоты дают значение k≈1011 моль-1·л·с-1, т.е. мгновенное протекание реакции. Причина того, что большинство реакций протекает намного медленнее в следующем: только малая доля всех соударений заканчивается химическим превращением.
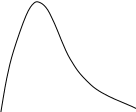
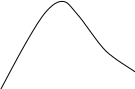
Анализ уравнения Аррениуса (3.5) показывает, что его постоянная Е имеет размерность энергии. Поэтому постоянную Е называют энергией активации (Еа). Было установлено, что Еа – энергия, которой должны обладать молекулы, чтобы соударение между ними было эффективным. Экспоненциальный множитель уравнения Аррениуса exp(-E/RT) был и в теоретическом выражении, полученном Максвеллом и Больцманом в рамках кинетической теории газов, для доли молекул, обладающих повышенной энергией. На рис.3.2 представлены кривые распределения молекул газа по кинетической энергии при двух разных температурах. В этом графике площадь между каждой кривой и осью абсцисс пропорциональна всему количеству молекул газа. Заштрихованная площадь соответствует доле частиц, обладающих повышенной энергией (≥Е), которая в выводе Максвелла и Больцмана приблизительно определяется значением exp(-E/RT). При этом, если с увеличением Т (Т2>Т1) средняя энергия молекул растет пропорционально температуре, то доля молекул с высокими значениями энергии растет быстрее за счет уменьшения доли молекул с малыми значениями энергии. Именно этим объясняется температурная зависимость скорости химических реакций (3.4). Частицы с энергией ≥Е называют активными, и только они вступают в химическое взаимодействие.
Доля молекул
с энергией ≥Е
Е
Энергия молекул х
Т1
Т2






1 ... 5 6 7 8 9 10 11 12 ... 15