ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 07.12.2023
Просмотров: 289
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
оС. При этой температуре твердые кадмий и висмут выпадают вместе, горизонтальный участок F и точка К при 140 оС; таким образом, этот состав является эвтектическим.
Температуры появления новых фаз, найденные по перегибам кривых охлаждения, затем переносят на диаграмму температура-состав, как показано в правой части рис.2.5. В области выше JKL существует одна жидкая фаза, и С=К-Ф+п=2-1+1=2. Вдоль линии JK выкристаллизовывается висмут, а вдоль LK – кадмий. Следовательно, вдоль линии JK и в области под нею вплоть до эвтектической температуры К имеются две фазы – твердый висмут и раствор, состав которого определяется температурой. Поскольку С=2-2+1=1, система моновариантна. Если указать одну из переменных, т.е. температуру или состав жидкой фазы, то другую переменную можно найти на линии JK. Вдоль линии KL и в области под ней также имеются две фазы – твердый кадмий и раствор; соответственно этому С=1.
В эвтектической точке К сосуществуют три фазы – твердый висмут, твердый кадмий и раствор, содержащий 0,4 кадмия. Здесь С=2-3+1=0; таким образом, система в этой точке инвариантна. Существуют только одна температура и один состав раствора, при которых эти три фазы могут находиться в равновесии при данном постоянном давлении.
Область ниже эвтектической температуры К двухфазная, в ней присутствуют твердые висмут и кадмий; С=2-2+1=1. Для полного описания состояния системы при данном постоянном давлении нужно указать лишь температуру. Отношение висмута к кадмию может изменяться, но здесь есть только чистый висмут и чистый кадмий, и поэтому нет необходимости указывать концентрации.
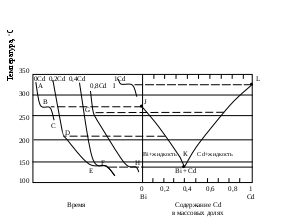
Рис.2.5. Кривые охлаждения и фазовая диаграмма
температура-состав для системы висмут – кадмий
В некоторых случаях компоненты бинарных систем могут образовывать между собой химические соединения, плавящиеся без разложения на другое твердое вещество и жидкую фазу. В таких случаях на диаграмме состав – температура появляется максимум, как показано на рис.2.6 для системы цинк-магний, и говорят, что это соединение плавится конгруэнтно. Точка на оси составов, соответствующая максимуму температуры, представляет состав соединения. Если концентрация выражена в мольных долях, то такие максимумы появляются при содержании одного из компонентов, равном 0,5; 0,33; 0,25 и т.д., что соответствует целочисленным отношениям компонентов – 1:1, 1:2, 1:3 и т.д. Диаграмма на рис.2.6 похожа на две помещенные рядом диаграммы уже рассмотренного типа, правда они несколько различаются. В данном случае кривая жидкости имеет горизонтальную касательную в точке плавления соединения MgZn
2, тогда как в точках плавления чистых компонентов наклон не равен нулю. Это значит, что если в какой-то системе А-В существует конгруэнтно плавящееся соединение АВ, то добавки очень малых количеств А или В не будут понижать его точку плавления (или точку замерзания).
Если компоненты бинарной системы образуют химическое соединение, плавящееся с разложением, то говорят, что это соединение плавится инконгруэнтно. В таком случае при нагревании системы до определенной температуры вместо плавления происходит разложение соединения на другое твердое соединение и раствор.
700
Жидкость 650 оС
J Е
600 С
590 оС
F H G
500
MgZn2 K Mg +
410 оС + раствор MgZn2 + раствор
A B раствор
380 оC
Zn +
300 раствор L D
Zn + MgZn2 MgZn2 + Mg
200 M I
0 0,2 0,4 0,6 0,8 1
Zn Содержание Mg, мольн. доли Mg














Рис. 2.6. Диаграмма температура – состав с
максимумом для системы цинк - магний
Такая точка плавления, называемая инконгруэнтной, изображена на рис.2.7, который представляет часть фазовой диаграммы для системы сульфат натрия – вода.
100
D
Жидкость Жидкость + Na2SO4
Na2SO4∙10H2O
C
32,38 oC
A Жидкость +
0 B Na2SO4 ∙ 10H2O
-1,286 Na2SO4 +
лед + Na2SO4 ∙ 10H2O Na2SO4 ∙ 10H2O
0 0,05 0,1 0,15
Содержание Na2SO4, мольн. доли











Рис.2.7. Часть фазовой диаграммы для системы Na2SO4 - H2O,
показывающая инкогруэнтное плавление Na2SO4∙10H2O
с образованием ромбического безводного Na2SO4
Если нагревать чистый Na2SO4∙10H2O, то при 32,38 оС он превращается в безводный Na2SO4 и раствор состава С. Линия ВС показывает растворимость Na2SO4∙10H2O в воде, а линия СD – растворимость Na2SO4 в воде. Рис. 2.7 объясняет, почему происходит нарушение непрерывности на кривой BCD для сульфата натрия в воде.
Когда три фазы – Na2SO4, Na2SO4∙10H2O и насыщенный раствор – находятся в равновесии, система инвариантна.
В ряде случаев компоненты бинарных систем могут быть неограниченно растворимы друг в друге как в жидком, так и в твердом состоянии. Пример диаграммы такой системы показан на рис. 2.8 для компонентов: золото-платина. Две линии на этой диаграмме дают состав жидких (верхняя линия) и твердых (нижняя линия) растворов, находящихся в равновесии. При анализе таких диаграмм следует помнить, что жидкая фаза богаче тем компонентом смеси, который имеет более низкую точку плавления. В области над верхней линией на оба металла находятся в виде жидкого раствора, а под нижней линией – в виде твердого раствора. Верхняя кривая представляет собой кривую затвердевания жидкости, а нижняя – кривую плавления твердого раствора. Пространство между двумя кривыми является областью равновесных смесей двух растворов – жидкого и твердого. Например, смесь, содержащая 0,5 золота и 0,5 платины, в момент равновесия при 1400
оС будет состоять из двух фаз: твердого раствора, содержащего 0,7 платины, и жидкого раствора, содержащего 0,28 платины. Если бы исходная смесь содержала 0,6 платины, то при 1400 оС образовывались бы те же два раствора, твердый и жидкий, того же состава, т.е. содержащих 0,7 и 0,28 платины, но количество твердого раствора в соответствии с правилом рычага, было бы больше, чем в первом случае.
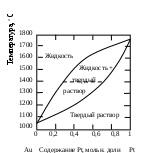
Рис. 2.8. Фазовая диаграмма для системы золото-платина,
образующей твердые растворы
2.3.2. Равновесие пар - жидкий раствор нелетучего вещества
Французский физико-химик Ф.М. Рауль в 1884 году экспериментально установил, что для идеальных растворов при постоянной температуре давление насыщенного пара растворителя над бинарным раствором (р) меньше чем над чистым растворителем (ро). При этом он нашел соотношение, котрое носит название закона Рауля:
р=роX, (2.3)
где X - мольная доля раствoрителя в растворе. Давление насыщенного пара растворителя над раствором равно произведению его давления над чистым растворителем на его мольную долю в растворе.
В настоящее время (2.3) выводится теоретически из равенства химических потенциалов растворителя в растворе (Р ) и в насыщенном паре (п):
Р = п. (2.4)
Действительно, если продифференцировать равенство (2.4) с учетом (1.128) и (1.129), то получится следующее равенство:
dln p = dln X.
Если далее провести интегрирование последнего равенства в пределах от давления пара растворителя над чистым растворителем ро до давления над раствором р и соответственно от мольной доли растворителя в чистом растворителе Хо=1 до его мольной доли в растворе Х, то получается соотношение (2.3), т.е. закон Рауля:
ln p - ln pо = ln X - ln Xо,
т.к. ln Xо = 0, то
p / pо = X или p = pоX .
Сумма мольных долей растворителя и растворенного вещества (Xв) бинарного раствора равна 1 (или X = 1-Xв), поэтому вместо последнего равенства вначале получим:
откуда следует:
ро – р = роXв или Δр/ро = Xв. (2.5)
Другими словами, относительное понижение давления пара растворителя над бинарным раствором равно мольной доле растворенного вещества. Формулы (2.3) и (2.5) отражают два способа выражения закона Рауля. Поскольку мольная доля растворителя в растворе всегда меньше единицы, давление его пара над раствором всегда меньше давления его пара над чистым растворителем. Чем более концентрированный раствор, тем значительнее снижение давления пара растворителя. Давление пара растворителя над раствором относится к коллигативным свойствам растворов, т.е. к таким свойствам, которые не зависят от природы веществ, а зависят только от количеств их частиц.
 р
р
0,1013 МПа А • А'• А"•
ро В•
р′ О• ● В′
р″ О″•О′• • В″
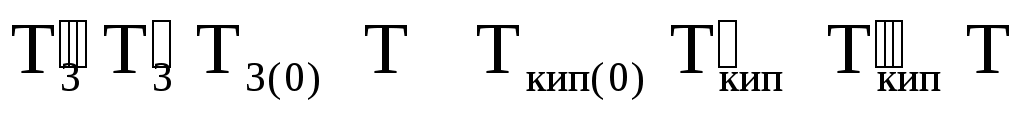
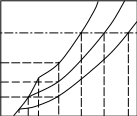
Рис. 2.9. Зависимость давления пара растворителя над раствором
и температуры кипения и замерзания раствора от
концентрации растворенного вещества:
ОА – чистый растворитель; О'А' – разбавленный раствор ;
;
О"А" – более концентрированный раствор
ЛЕКЦИЯ 9
В случае бинарных растворов нелетучих веществ давление пара определяется только растворителем и по (2.3) оно меньше ро. Поэтому для достижения точки кипения (когда давление насыщенного пара жидкости равно давлению окружающей среды, например атмосферному – 0,1013МПа) растворы нужно нагревать до более высоких температур, чем температура кипения чистого растворителя (рис.2.9). Видно, что кривая зависимости р(Т) с ростом концентрации (Хв) смещается вниз (точки В, В', В"), хотя профиль ее остается практически неизменным, а температура кипения (Ткип) при этом возрастает (точки А, А', А").
Рауль экспериментально установил соотношение зависимости увеличения температуры кипения растворов (ΔТкип) от их концентрации:
Tкип = Ткип – Ткип(о) = Кэ b, (2.6)
где Ткип – температура кипения раствора, Т кип(о) – температура кипения растворителя , b – моляльная концентрация раствора, Кэ – эбуллиоскопическая постоянная, характеризующая только растворитель (для воды Кэ = 0,52кг∙К/моль) и показывающая, чему равно ∆Ткип при b = 1 моль/кг. Поэтому все растворы различных неэлектролитов в одном и том же растворителе при одинаковой концентрации (b) кипят при одной и той же температуре. А в случае упаривания растворов с ростом их концентрации возрастает их температура кипения. В настоящее время уравнение (2.6) выведено теоретически и Кэ в нем имеет следующее значение:
где Мо – молярная масса растворителя,
Температуры появления новых фаз, найденные по перегибам кривых охлаждения, затем переносят на диаграмму температура-состав, как показано в правой части рис.2.5. В области выше JKL существует одна жидкая фаза, и С=К-Ф+п=2-1+1=2. Вдоль линии JK выкристаллизовывается висмут, а вдоль LK – кадмий. Следовательно, вдоль линии JK и в области под нею вплоть до эвтектической температуры К имеются две фазы – твердый висмут и раствор, состав которого определяется температурой. Поскольку С=2-2+1=1, система моновариантна. Если указать одну из переменных, т.е. температуру или состав жидкой фазы, то другую переменную можно найти на линии JK. Вдоль линии KL и в области под ней также имеются две фазы – твердый кадмий и раствор; соответственно этому С=1.
В эвтектической точке К сосуществуют три фазы – твердый висмут, твердый кадмий и раствор, содержащий 0,4 кадмия. Здесь С=2-3+1=0; таким образом, система в этой точке инвариантна. Существуют только одна температура и один состав раствора, при которых эти три фазы могут находиться в равновесии при данном постоянном давлении.
Область ниже эвтектической температуры К двухфазная, в ней присутствуют твердые висмут и кадмий; С=2-2+1=1. Для полного описания состояния системы при данном постоянном давлении нужно указать лишь температуру. Отношение висмута к кадмию может изменяться, но здесь есть только чистый висмут и чистый кадмий, и поэтому нет необходимости указывать концентрации.

Рис.2.5. Кривые охлаждения и фазовая диаграмма
температура-состав для системы висмут – кадмий
В некоторых случаях компоненты бинарных систем могут образовывать между собой химические соединения, плавящиеся без разложения на другое твердое вещество и жидкую фазу. В таких случаях на диаграмме состав – температура появляется максимум, как показано на рис.2.6 для системы цинк-магний, и говорят, что это соединение плавится конгруэнтно. Точка на оси составов, соответствующая максимуму температуры, представляет состав соединения. Если концентрация выражена в мольных долях, то такие максимумы появляются при содержании одного из компонентов, равном 0,5; 0,33; 0,25 и т.д., что соответствует целочисленным отношениям компонентов – 1:1, 1:2, 1:3 и т.д. Диаграмма на рис.2.6 похожа на две помещенные рядом диаграммы уже рассмотренного типа, правда они несколько различаются. В данном случае кривая жидкости имеет горизонтальную касательную в точке плавления соединения MgZn
2, тогда как в точках плавления чистых компонентов наклон не равен нулю. Это значит, что если в какой-то системе А-В существует конгруэнтно плавящееся соединение АВ, то добавки очень малых количеств А или В не будут понижать его точку плавления (или точку замерзания).
Если компоненты бинарной системы образуют химическое соединение, плавящееся с разложением, то говорят, что это соединение плавится инконгруэнтно. В таком случае при нагревании системы до определенной температуры вместо плавления происходит разложение соединения на другое твердое соединение и раствор.
700
Жидкость 650 оС
J Е
600 С
590 оС
F H G
500
MgZn2 K Mg +
410 оС + раствор MgZn2 + раствор
A B раствор
380 оC
Zn +
300 раствор L D
Zn + MgZn2 MgZn2 + Mg
200 M I
0 0,2 0,4 0,6 0,8 1
Zn Содержание Mg, мольн. доли Mg














Рис. 2.6. Диаграмма температура – состав с
максимумом для системы цинк - магний
Такая точка плавления, называемая инконгруэнтной, изображена на рис.2.7, который представляет часть фазовой диаграммы для системы сульфат натрия – вода.
100
D
Жидкость Жидкость + Na2SO4
Na2SO4∙10H2O
C
32,38 oC
A Жидкость +
0 B Na2SO4 ∙ 10H2O
-1,286 Na2SO4 +
лед + Na2SO4 ∙ 10H2O Na2SO4 ∙ 10H2O
0 0,05 0,1 0,15
Содержание Na2SO4, мольн. доли











Рис.2.7. Часть фазовой диаграммы для системы Na2SO4 - H2O,
показывающая инкогруэнтное плавление Na2SO4∙10H2O
с образованием ромбического безводного Na2SO4
Если нагревать чистый Na2SO4∙10H2O, то при 32,38 оС он превращается в безводный Na2SO4 и раствор состава С. Линия ВС показывает растворимость Na2SO4∙10H2O в воде, а линия СD – растворимость Na2SO4 в воде. Рис. 2.7 объясняет, почему происходит нарушение непрерывности на кривой BCD для сульфата натрия в воде.
Когда три фазы – Na2SO4, Na2SO4∙10H2O и насыщенный раствор – находятся в равновесии, система инвариантна.
В ряде случаев компоненты бинарных систем могут быть неограниченно растворимы друг в друге как в жидком, так и в твердом состоянии. Пример диаграммы такой системы показан на рис. 2.8 для компонентов: золото-платина. Две линии на этой диаграмме дают состав жидких (верхняя линия) и твердых (нижняя линия) растворов, находящихся в равновесии. При анализе таких диаграмм следует помнить, что жидкая фаза богаче тем компонентом смеси, который имеет более низкую точку плавления. В области над верхней линией на оба металла находятся в виде жидкого раствора, а под нижней линией – в виде твердого раствора. Верхняя кривая представляет собой кривую затвердевания жидкости, а нижняя – кривую плавления твердого раствора. Пространство между двумя кривыми является областью равновесных смесей двух растворов – жидкого и твердого. Например, смесь, содержащая 0,5 золота и 0,5 платины, в момент равновесия при 1400
оС будет состоять из двух фаз: твердого раствора, содержащего 0,7 платины, и жидкого раствора, содержащего 0,28 платины. Если бы исходная смесь содержала 0,6 платины, то при 1400 оС образовывались бы те же два раствора, твердый и жидкий, того же состава, т.е. содержащих 0,7 и 0,28 платины, но количество твердого раствора в соответствии с правилом рычага, было бы больше, чем в первом случае.

Рис. 2.8. Фазовая диаграмма для системы золото-платина,
образующей твердые растворы
2.3.2. Равновесие пар - жидкий раствор нелетучего вещества
Французский физико-химик Ф.М. Рауль в 1884 году экспериментально установил, что для идеальных растворов при постоянной температуре давление насыщенного пара растворителя над бинарным раствором (р) меньше чем над чистым растворителем (ро). При этом он нашел соотношение, котрое носит название закона Рауля:
р=роX, (2.3)
где X - мольная доля раствoрителя в растворе. Давление насыщенного пара растворителя над раствором равно произведению его давления над чистым растворителем на его мольную долю в растворе.
В настоящее время (2.3) выводится теоретически из равенства химических потенциалов растворителя в растворе (Р ) и в насыщенном паре (п):
Р = п. (2.4)
Действительно, если продифференцировать равенство (2.4) с учетом (1.128) и (1.129), то получится следующее равенство:
dln p = dln X.
Если далее провести интегрирование последнего равенства в пределах от давления пара растворителя над чистым растворителем ро до давления над раствором р и соответственно от мольной доли растворителя в чистом растворителе Хо=1 до его мольной доли в растворе Х, то получается соотношение (2.3), т.е. закон Рауля:
ln p - ln pо = ln X - ln Xо,
т.к. ln Xо = 0, то
p / pо = X или p = pоX .
Сумма мольных долей растворителя и растворенного вещества (Xв) бинарного раствора равна 1 (или X = 1-Xв), поэтому вместо последнего равенства вначале получим:
р = рo(1- Xв) или р = ро – роXв,
откуда следует:
ро – р = роXв или Δр/ро = Xв. (2.5)
Другими словами, относительное понижение давления пара растворителя над бинарным раствором равно мольной доле растворенного вещества. Формулы (2.3) и (2.5) отражают два способа выражения закона Рауля. Поскольку мольная доля растворителя в растворе всегда меньше единицы, давление его пара над раствором всегда меньше давления его пара над чистым растворителем. Чем более концентрированный раствор, тем значительнее снижение давления пара растворителя. Давление пара растворителя над раствором относится к коллигативным свойствам растворов, т.е. к таким свойствам, которые не зависят от природы веществ, а зависят только от количеств их частиц.
 р
р0,1013 МПа А • А'• А"•
ро В•
р′ О• ● В′
р″ О″•О′• • В″
Рис. 2.9. Зависимость давления пара растворителя над раствором
и температуры кипения и замерзания раствора от
концентрации растворенного вещества:
ОА – чистый растворитель; О'А' – разбавленный раствор
О"А" – более концентрированный раствор
ЛЕКЦИЯ 9
В случае бинарных растворов нелетучих веществ давление пара определяется только растворителем и по (2.3) оно меньше ро. Поэтому для достижения точки кипения (когда давление насыщенного пара жидкости равно давлению окружающей среды, например атмосферному – 0,1013МПа) растворы нужно нагревать до более высоких температур, чем температура кипения чистого растворителя (рис.2.9). Видно, что кривая зависимости р(Т) с ростом концентрации (Хв) смещается вниз (точки В, В', В"), хотя профиль ее остается практически неизменным, а температура кипения (Ткип) при этом возрастает (точки А, А', А").
Рауль экспериментально установил соотношение зависимости увеличения температуры кипения растворов (ΔТкип) от их концентрации:
Tкип = Ткип – Ткип(о) = Кэ b, (2.6)
где Ткип – температура кипения раствора, Т кип(о) – температура кипения растворителя , b – моляльная концентрация раствора, Кэ – эбуллиоскопическая постоянная, характеризующая только растворитель (для воды Кэ = 0,52кг∙К/моль) и показывающая, чему равно ∆Ткип при b = 1 моль/кг. Поэтому все растворы различных неэлектролитов в одном и том же растворителе при одинаковой концентрации (b) кипят при одной и той же температуре. А в случае упаривания растворов с ростом их концентрации возрастает их температура кипения. В настоящее время уравнение (2.6) выведено теоретически и Кэ в нем имеет следующее значение:
 (2.7)
(2.7)
где Мо – молярная масса растворителя,