ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.12.2023
Просмотров: 537
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
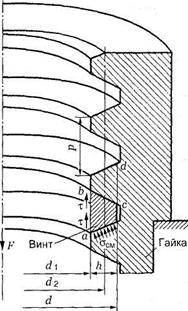
Рис. 46. К расчету резьбы на срез
Расчет резьбы по напряжению смятия.
Условие прочности витка резьбы по смятию:
а) для гайки
б) для винта
где F - осевая сила, действующая на болт, d2 - среднийдиаметр резьбы, h - высота витка, z - число витков резьбы в гайке, [σ]смв - допускаемое напряжение смятия материала винта, [σ]смг - допускаемое напряжение смятия материала гайки.
Расчет резьбы по напряжению среза.
Проверочный расчет. Условие прочности
τср≤[τ]ср,
где τср — расчетное напряжение среза в резьбе; [τ]ср — допускаемое напряжение среза в резьбе.
Для винта:
для гайки
здесь F — осевое усилие, действующее на болт; d1 — внутренний диаметр резьбы; d — наружный диаметр резьбы; Н — высота гайки; K=cd/P — коэффициент, учитывающий тип резьбы (K=0,8 — для треугольной резьбы; К= 0,5 — для прямоугольной и К= 0,65 — для трапецеидальной резьбы).
Из условия равнопрочности резьбы и стержня винта определяются высота гайки, нормы на глубину завинчивания винтов и шпилек в деталь и прочие размеры. Учитывая сложность напряженного состояния резьбы, а, также предусматривая ослабление резьбы от истирания и возможных повреждений при завинчивании, высоту стандартных гаек крепежных изделий принимают H≈0,8d1. По тем же соображениям устанавливают нормы завинчивания винтов и шпилек в детали H=d1 – в стальные детали, H=1,5d1 – в чугунные и силуминовые детали.
Расчет незатянутого болта, нагруженного внешней растягивающей силой
Этот случай встречается редко. Примером служит нарезанный участок крюка для подвешивания груза. Опасным бывает сечение, ослабленное резьбой. На рис. 48 показан пример такого резьбового соединения. Стержень крюка работает только на растяжение. Резьбовое соединение, рассматриваемое в данном случае, называют ненапряженным. Такие соединения способны воспринимать только статическую нагрузку. Опасным будет сечение, ослабленное резьбой. Статическая прочность стержня с резьбой выше (в среднем на 10%), чем гладкого стержня с диаметром, равным внутреннему диаметру d1.
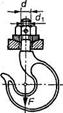
Рис.48. Грузовой крюк с обоймой
Проверочный расчет ненапряженного болтового соединения. Условие прочности на растяжение:
где σp и [σ]p — соответственно расчетное и допускаемое напряжения растяжения в поперечном сечении нарезанной части болта; F — растягивающая сила; d1— внутренний диаметр резьбы болта.
Проектировочный расчет ненапряженного болтового соединения сводится к определению внутреннего диаметра резьбы d1, из условия прочности (9):
где [σ]p=σT/[s]T — допускаемое напряжение на растяжение; σT — предел текучести материала болта; [s]T — допускаемый коэффициент запаса прочности. Для болтов из углеродистой стали принимают [s]T =1,5÷3,0. Большие значения коэффициента запаса [s]T принимают при невысокой точности определения величины нагрузки F или для конструкций повышенной ответственности.
Болтовое соединение нагружено силами в плоскости стыка
Условием надежности соединения является отсутствие сдвига деталей в стыке. Примером может служить соединение двух полумуфт в дисковой муфте. Конструкция может быть собрана по двум вариантам.
Расчет болта, нагруженного поперечной силой Frпри установке его с зазором (рис. 52).
В этом случае болт ставится с зазором в отверстие деталей.
Для обеспечения неподвижности соединяемых листов 1, 2, 3 болт затягивают силой затяжки F3. Во избежание работы болта на изгиб его следует затянуть так сильно, чтобы силы трения на стыках деталей были больше сдвигающих сил Fr.
Основные допущения.
1) Деформация соединяемых деталей не учитывается, то есть детали принимают абсолютно жесткими.
2) Внешние нагрузки передаются от одной детали на другую локально, через зоны, расположенные вокруг болтов.
3) Расчет ведут на предотвращение сдвига деталей по условию неподвижности стыка.
Основным критерием расчета является условие неподвижности стыка.
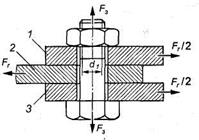
Рис. 52. К расчету болтов соединения, несущего поперечную нагрузку.
Болт установлен с зазором
Обычно силу трения принимают с запасом: Ff= KFr. (К –коэффициент запаса по сдвигу деталей, К = 1,3 – 1,5 при статической нагрузке, К = 1,8 – 2 при переменной нагрузке).
Найдем требуемую затяжку болта. Учтем, что сила затяжки болта может создавать нормальное давление на i трущихся поверхностях (на рис. 52)
где i– число плоскостей стыка деталей (на рис.52 – i = 2; при соединении только двух деталей i = 1); f – коэффициент трения в стыке (f = 0,15 – 0,2 для сухих чугунных и стальных поверхностей);
Как известно при затяжке болт работает на растяжение и кручение поэтому прочность болта оценивают по эквивалентному напряжению. Так как внешняя нагрузка не передается на болт, его рассчитывают только на статическую прочность по силе затяжки даже при переменной внешней нагрузке. Влияние переменной нагрузки учитывают путем выбора повышенных значений коэффициента запаса.
Проектировочный расчет болта:
внутренний диаметр резьбы
Расчет болта, нагруженного поперечной силой, с установкой его без зазора (рис. 53).
Основные допущения.
1) Деформации деталей не учитываются, то есть считают детали абсолютно жесткими.
2) Внешние нагрузки передаются с одной детали на другую локально, через зоны, расположенные вокруг болтов.
3) Силы трения, связанные с затяжкой болтов, не учитываются.
4) Основным критерием расчета является условие неподвижности стыка.
5) При установке болта без зазора неподвижность обеспечивается сопротивлением болта срезу и смятию.
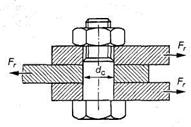
Рис. 53. К расчету болтов соединения, несущего поперечную нагрузку.
Болт установлен без зазора
В этом случае отверстие калибруют разверткой, а диаметр стержня болта выполняют с допуском, обеспечивающим беззазорную посадку. При расчете прочности данного соединения не учитывают силы трения в стыке, так как затяжка болта не контролируется. В общем случае болт можно заменить штифтом. Стержень болта рассчитывают по напряжениям среза и смятия.
Условие прочности
где
[τ]ср=(0,2÷0,3)σT.
Проектировочный расчет.
Диаметр стержня из условия среза
Расчет болтов при внецентренно приложенной силе
Рассмотрим два случая:
1. Поставлен болт с костыльной головкой. В винтах с эксцентричной (костыльной) головкой под действием силы Fзат возникают напряжения растяжения σр и σи (рис. 55).
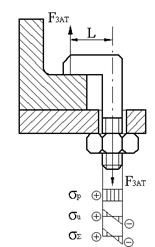
Рис.55. Болт с костыльной головкой
Суммарное напряжение в наиболее опасной точке
Коэффициент 1,3 учитывает напряжения кручения стержня болта от момента трения в резьбе Тр.
Из формулы следует, что с увеличением эксцентриситета е напряжение в болте будет возрастать. При эксцентричном приложении нагрузки суммарные напряжения в болте могут во много раз превышать напряжения растяжения. Например, при эксцентриситете e=0,5dp суммарные напряжения σΣ=5,3σp.
В связи с этим следует избегать применения болтов с эксцентричными головками.
2.Опорные поверхности под гайку и головку болта непараллельны(рис. 55.1).
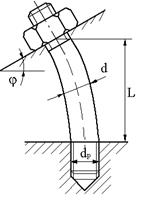
Рис.55.1. Опорные поверхности под гайку и головку болта непараллельны
За напряженное состояние винта в первом приближении принимают чистый изгиб, т.к. изгибные напряжения во много раз превышают напряжения растяжения. По заданному углу наклона упругой линии определяем изгибающий момент на винте
где l – деформируемая длина винта; Е – модуль упругости материала винта; I=πd2/64 – момент инерции сечения стержня винта.
Напряжения изгиба в винте (рис.55.1)
Напряжения изгиба в резьбовой части
Для уменьшения напряжений изгиба повышают точность изготовления (вводят допуски на перекосы опорных поверхностей, на биение торца) или применяют специальные конструкции – сферические или косые шайбы.
Расчет болтов при внецентренно приложенной силе
.Опорные поверхности под гайку и головку болта непараллельны(рис. 55.1).

Рис.55.1. Опорные поверхности под гайку и головку болта