Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

Внутренние усилия должны быть так распределены по сечению, чтобы деформированные поверхности сечения при совмещении правой и левой частей тела в точности совпадали. Это требование в механике твердого деформируемого тела носит название условия неразрывности деформаций.

Рассмотрим отдельно какую-либо из отсеченных частей бруса, например левую. Внутренние силы, возникающие в сечении целого бруса по отношению к рассматриваемой отсеченной части бруса, являются внешними и дополняют систему заданных внешних сил до равновесной. Приведем систему внутренних сил к центру тяжести сечения (рис. 1.6, б). В результате получим главный вектор R и главный момент M.

Выберем систему координат так, чтобы ось z совпала с нормалью к сечению (располагалась вдоль оси элемента), а оси у и x лежали в плоскости нормального сечения. Разложив главный вектор и главный момент по осям координат, получим составляющие: три силы и три момента. Эти составляющие называют внутренними силовыми факторами в сечении бруса, каждая из которых имеет свое наименование: N - нормальная сила; Q_y и Q_z - поперечные силы; Т - крутящий момент; M_zи М_у - изгибающие моменты относительно осей x и y (рис. 1.6, в).

При известной нагрузке все шесть внутренних силовых факторов могут быть определены из уравнений равновесия составленных для рассматриваемой части бруса. Заметим, что в каждое уравнение войдут проекции на соответствующую ось (или моменты относительно оси) всех внешних сил, приложенных к рассматриваемой части, и только один из внутренних силовых факторов.

ΣZ = ΣF_z^отс + N = 0;      Σm_z = ΣM_z^отс + T = 0;

ΣY = ΣF_y^отс + Q_y = 0;    Σm_y = ΣM_y^отс + M_y = 0;

ΣX = ΣF_x^отс + Q_x = 0;     Σm_x = ΣM_x^отс + M_x = 0.

Уравнения равновесия позволяют сформулировать правило определения каждого из внутренних силовых факторов:

Продольная сила в произвольном поперечном сечении бруса численно равна алгебраической сумме проекций на ось z, всех внешних сил, действующих на одну из  отсеченных (левую или правую) частей бруса.

N = ΣF_z^отс.

То же для определения поперечных сил 

---

Q_y и Q_x,,только проектировать внешние силы необходимо на оси y и x.

Q_y = ΣF_y^отс,

Q_x = ΣF_x^отс.

Изгибающие моменты M_x и M_y и крутящий момент T, численно равны алгебраической сумме моментов всех сил по одну сторону от сечения, относительно соответствующих осей x, y и z.

T = ΣM_z^отс,

M_x = ΣM_x^отс,

M_y = ΣM_y^отс.

Для установления знака внутреннего силового фактора будем придерживаться следующих правил:

Условимся продольную силу считать положительной, если она вызывает растяжение, т.е. направлена от сечения и отрицательной, если она вызывает сжатие, т. е. направлена к сечению.

При решении задач знак N удобнее устанавливать в зависимости от направления внешних сил. Если внешняя сила, направлена в противоположную от сечения сторону, то она вызывает в нем положительную продольную силу (растяжение), и наоборот, если внешняя сила, направлена к сечению, то она вызывает в нем отрицательную продольную силу (сжатие) (рис. 1.7, а).

 Поперечную силу Q будем считать положительной, если она направлена так, что стремиться повернуть отсеченную часть бруса по ходу часовой стрелки (рис. 1.7, б), и отрицательной, если - против хода часовой стрелки.

Согласно этому правилу внешняя сила, стремящаяся повернуть рассматриваемую часть бруса относительно сечения по ходу часовой стрелки, вызывает в сечении положительную поперечную силу

Крутящий момент Т будем  считать положительным, если при взгляде со стороны внешней нормали на рассматриваемое сечение он направлен по ходу часовой стрелки или внешний скручивающий момент направлен против хода часовой стрелки (рис.1.7, в).

Изгибающий момент Mx считается положительным, если он  вызывает растяжение нижних волокон рассматриваемой части бруса. В противном случае изгибающий момент считается отрицательным (рис. 1.7, г).

---

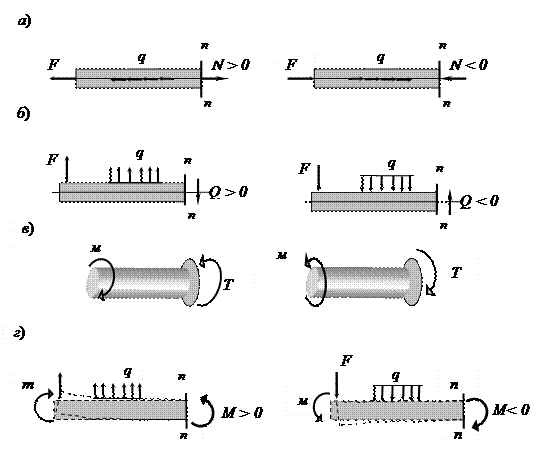
Рис. 1.7. Виды сопротивлений:

а) растяжение (сжатие); б) сдвиг; в) кручение; г) изгиб

 

Согласно принятому правилу знаков для изгибающего момента, если внешняя сила, приложенная к рассматриваемой части бруса изгибает участок, расположенный между сечением точкой ее приложения выпуклостью вниз, то изгибающий момент положительный. Отрицательному значению изгибающего момента соответствует противоположное направление выпуклости балки

Таким образом, метод сечений позволяет найти значения внутренних силовых факторов и установить вид нагружения в любом сечении бруса при действии любой нагрузки. Для этого необходимо выполнить следующее:

1. Мысленно рассекаем брус на две части в пределах исследуемого i–го участка.

2. Оставляем ту часть бруса, на которую действует меньше сил.

3. Заменяем действие условно отброшенной части бруса положительными внутренними силовыми факторами, приведенными к центру тяжести исследуемого сечения бруса.

4. Выберем для оставленной части бруса скользящую систему координат (начало координат совмещаем с границей участка, положение исследуемого сечения определяется координатой z_i, где 0≤z_i≤c и c – длина i-го участка).

5. Определяем искомые внутренние силовые факторы из уравнений равновесия ΣZ = 0;  ΣY = 0;   ΣX = 0;   Σm_z = 0;   Σm_y = 0;   Σm_x = 0, которые составляем для оставленной части бруса.

Проверка правильности определения усилий ведется в двух направлениях:

а) выполнение условий равновесия, не использованных при определении внутренних усилий;

б) проверка равновесия части тела, которая не рассматривалась при решении задачи.

В зависимости от вида внутренних силовых факторов, возникающих в сечении, различают различные следующие виды нагружениябруса.

- Растяжение или сжатие. Действует только продольная сила N.

- Кручение. Действует только крутящий момент T.

- Сдвиг. Действует  только поперечная сила Q_x или Q_y

- Изгиб. Действует только изгибающий момент M_x или M_y(чистый изгиб), при действии изгибающего момента и поперечной силы (поперечный изгиб).

- Сложное сопротивление. Одновременное действие нескольких силовых факторов. Например, 

---

M_x и T, M и N.

Итак, внутренние усилия в сечении есть функции параметров, определяющих положение сечения в теле, и нагрузок по одну сторону от сечения. Эти функции могут быть представлены аналитически или графически. График, показывающий изменение внутреннего усилия в зависимости от положения сечения, называется эпюрой. Ординаты усилий в определенном масштабе откладывают от линии, соответствующей оси бруса.

3. Дифференциальные уравнения равновесия для внутренних усилий в поперечных сечениях стержней

В общем случае нагрузка на стержень может быть задана интенсивностью сил с составляющими n, q_y, q_z, и интенсивностью моментов с составляющими t, m_y, m_z. Возможна также нагрузка, сосредоточенная в отдельных точках. Для бесконечно малой части стержня (рис.8) составим дифференциальные уравнения равновесия.



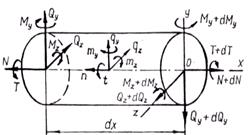
Рис. 1.8

 

Из условий ΣX=0,  ΣY=0,  ΣZ=0,  ΣM_x=0, следуют уравнения:

Из условий ΣX=0,  ΣY=0,  ΣZ=0,  ΣM_x=0, следуют уравнения:



Из условий ΣM_y=0, ΣM_z=0 получаем:





откуда, пренебрегая бесконечно малыми второго порядка, находим



Подставляя выражения Q_y и Q_z в соответствующие дифференциальные уравнения, получаем



Интегрируя полученные шесть уравнений, находим выражения для внутренних усилий:

---

Постоянные интегрирования С_i (i=1,2,...,6) определяются из граничных условий для рассматриваемых внутренних усилий.

Поскольку дифференциальные уравнения выражают равновесие любого бесконечно малого элемента стержня, то удовлетворение им означает выполнение условий равновесия стержня в целом.

Дифференциальные зависимости используются для проверки результатов, полученных с помощью алгебраических уравнений равновесия. Они позволяют, например, по эпюре M_z(M_y) определить характер эпюры Q_y(Q_z). В частности, на участках, где m_z=0 (m_y=0), т.е. при соблюдении зависимостей



можно установить, что при М_z = const имеем Q_y= 0(при М_y=const имеем Q_z = 0). Переменная величина M_z(M_y) достигает экстремальных значений в точках, где Q_y= 0(Q_z= 0).

При определении внутренних усилий из уравнений равновесия целесообразно нагрузку на поверхности переносить в соответствующие точки на оси стержня с соблюдением условий статической эквивалентности. Полученная таким образом силовая схема является составной частью так называемой расчетной схемы (системы), когда брус представляется его осью. 

3. 
   Допущения, применяемые в сопротивлении материалов
   

Для построения теории сопротивления материалов принимают некоторые понятия и допущения относительно структуры и свойств материалов, а также о характере деформаций. Приведем основные из них.

1. В сопротивлении материалов принято рассматривать все материалы как однородную сплошную среду, независимо от их микроструктуры.

Под однородностью материала понимают независимость его свойств от величины выделенного из тела объема. И хотя в действительности реальный материал, как правило, неоднороден (уже в силу его молекулярного строения), тем не менее, указанная особенность не является существенной, поскольку в сопротивлении материалов рассматриваются конструкции, размеры которых существенно превышают не только межатомные расстояния, но и размеры кристаллических зерен.

---