Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 713
Скачиваний: 1
СОДЕРЖАНИЕ
7.2.Изгиб с растяжением (сжатием)………………….……………………………….92
7.3.Внецентренное сжатие или растяжение………………….………………………93
Вопросы для самопроверки……………………………………………………………99
8.Прочность при переменных и циклически изменяющихся напряжениях…………………………………………………………………………….100
8.1.Усталость и выносливость материалов…………………….……………………100
8.2.Основные характеристики цикла и предел усталости……………….…………102
8.3.Расчет коэффициентов запаса усталостной прочности………………….……...104
Библиографический список………………………………………………..………152
АННОТАЦИЯ ДИСЦИПЛИНЫМЕХАНИКА. МОДУЛЬ ПРИКЛАДНАЯ МЕХАНИКА
1.9. Общие принципы расчета конструкции
3. Осевое растяжение – сжатие.
4. Геометрические характеристики плоских сечений
5.1. Основные понятия. Крутящий момент
Условие прочности при кручении вала круглого и кольцевого сечения
7.1.Расчет балки, подверженной косому или пространственному изгибу
7.2. Изгиб с растяжением (сжатием)
8. Прочность при переменных и циклически изменяющихся напряжениях
Соответствующие элементарные моменты относительно координатных осей x, y, z имеют вид:
Просуммировав бесконечно малые силы и моменты, действующие в сечении, получим выражения, связывающие внутренние силовые факторы с напряжениями:
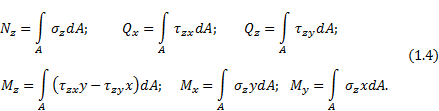
В соответствии с теоремой Вариньона, известной из теоретической механики, и зависимостью между напряжениями τ, и , выражение для можно записать в виде
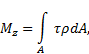
где
Интегральные зависимости (1.4) можно использовать для определения напряжений по найденным методом сечений внутренним силовым факторам при условии, что известны законы распределения напряжений по сечению. Поскольку эти законы зависят от вида деформации, то обратная задача (определение напряжений через внутренние усилия) решается путем совместного использования условий равновесия и условий деформирования тела. Задача становится статически неопределимой.
-
Перемещения и деформации
Под действием внешних сил твердые тела изменяют свою геометрическую форму, то есть деформируются. Если в теоретической механике тела считаются абсолютно жесткими, то в сопротивлении материалов тела обладают способностью деформироваться, т.е. под действием внешней нагрузки изменять свои начальные размеры и форму. Точки тела при этом неодинаково перемещаются в пространстве. Вектор , имеющий свое начало в точке А недеформированного состояния, а конец в т. деформированного состояния, называется вектором полного перемещения т. А (рис. 15, а). Его проекции на оси xyz называются осевыми перемещениями и обозначаются u, v и w, соответственно.
Для того, чтобы охарактеризовать интенсивность изменения формы и размеров тела, рассмотрим точки А и В его недеформированного состояния, расположенные на расстоянии S друг от друга (рис. 15, б).

Рис. 1.15
Пусть в результате изменения формы тела эти точки переместились в положение и , соответственно, а расстояние между ними увеличилось на величину S и составило S + S. Величина
называется линейной деформацией в точке А по направлению АВ. Если рассматривать деформации по направлениям координатных осей xyz, то в обозначения соответствующих проекций линейной деформации вводятся индексы , , .
Линейные деформации , , характеризуют изменения объема тела в процессе деформирования, а формоизменения тела угловыми деформациями. Для их определения рассмотрим прямой угол, образованный в недеформированном состоянии двумя отрезками ОD и ОС (рис. 1.15, б). При действии внешних сил указанный угол DOC изменится и примет новое значение . Величина
называется угловой деформацией, или сдвигом в точке О в плоскости СОD. Относительно координатных осей деформации сдвига обозначаются , , .
Линейные и угловые деформации – величины безразмерные. Деформацию , , часто называют относительной линейной деформацией, а , , – относительным сдвигом.
Положительными принимают линейную деформацию, соответствующую растяжению, и деформацию сдвига, отвечающую уменьшению первоначального угла пересечения отрезков. Полагая деформации малыми, мы можем в дальнейшем пренебрегать ими по сравнению с единицей, а также их высокими степенями по сравнению с первой степенью.
Совокупность линейных и угловых деформаций по различным направлениям и плоскостям в данной точке образует деформированное состояние в точке. В случае малых деформаций оно полностью определяется линейными деформациями трех взаимно перпендикулярных линейных элементов тела, проходящих через данную точку, и тремя деформациями сдвига этих линейных элементов. Соответствующие шесть независимых скалярных величин определяют тензор деформаций:
Главные оси деформации
– три взаимно перпендикулярные прямые, проходящие через данную точку тела и совпадающие по направлениям с такими тремя линейными элементами тела, которые остаются взаимно перпендикулярными и после деформации. Линейные деформации по направлениям этих осей называются главными деформациями и обозначаются ε1, ε2, ε3 (ε1≥ε2≥ε3).
Следует подчеркнуть, что в сопротивлении материалов слово деформация имеет данное выше строгое определение и выступает как количественная мера изменения геометрических размеров в окрестностях точки.
-
Закон Гука и принцип независимости действия сил
Многочисленные экспериментальные наблюдения за поведением деформируемых тел показывают, что в определенных диапазонах перемещения точек тела пропорциональны действующим на него нагрузкам. Впервые указанная закономерность была высказана в 1776 году английским ученым Р.Гуком в формулировке «ut tensio sic vis»- «какого растяжение - такова и сила» и носит название закона Гука.
В соответствии с этим законом перемещение произвольно взятой точки А (рис. 15, а) нагруженного тела по некоторому направлению, например, по оси x, а может быть выражено следующим образом:
где Р - сила, под действием которой происходит перемещение u; - коэффициент пропорциональности между силой и перемещением.
Очевидно, что коэффициент зависит от физико-механических свойств материала, взаимного расположения точки А и точки приложения и направления силы Р, а также от геометрических особенностей системы. Таким образом, последнее выражение следует рассматривать как закон Гука для данной системы.
В современной трактовке закон Гука определяет линейную зависимость между напряжениями и деформациями, а не между силой и перемещением.
Касательные напряжения τ вызывают угловые деформации γ, причем при малых деформациях они не влияют на изменение линейных размеров и, следовательно, на линейные деформации. Нормальное напряжение σ не влияет на угловые деформации, так как при этом изменяются только линейные размеры отрезков, а не углы между ними.
Параметры E и G, входящие в эти формулы, называют модулями упругости материала соответственно первого и второго рода. Они характеризуют его сопротивляемость деформированию, или жесткость в упругой стадии деформации. При одном и том же напряжении деформации больше у того материала, у которого меньше модуль упругости. Численные значения
E и G для каждого конструктивного материала определяются экспериментально. Они имеют размерности напряжений. На практике удобно использовать единицы, кратные паскалю: мегапаскаль (1 МПа=106 Па) и гигапаскаль (1 ГПа=109 Па).
При растяжении или сжатии одновременно с продольной деформацией ε =∆l/l (рис. 16, а), в элементе возникает поперечная деформация = -∆а/а.
Отношение
называют коэффициентом Пуассона.
Величины коэффициента Пуассона и модуля упругости для различных материалов определяют опытным путем и их значения приведены в ГОСТ. Между модулем упругости и модулем сдвига существует зависимость
Установим связь между нормальными напряжениями и линейными деформациями, справедливые для любого напряженного состояния. Рассмотрим бесконечно малый элемент, имеющий форму кубика, на гранях которого возникают напряжения растяжения σx, σy, σz. При действии только напряжения σx, элемент получает продольную деформацию в направлении оси х, равную, согласно закону Гука, σx/Е (рис. 16,б). Одновременно его размеры вдоль осей y и z уменьшатся, при этом соответствующие поперечные деформации будут равны
Аналогичное действие оказывает растягивающие напряжения σy и σz.. Каждое из них вызывает продольную деформацию в своем направлении σу/Е и σz/Е и поперечные деформации по двум другим направлениям (рис. 16,в, г).
Суммируя деформации в направлениях каждой оси, получаем
Эти зависимости представляют собой математические выражения обобщенного закона Гука. Напряжения σ
x, σy, σz следует подставлять в формулы со своим знаком.
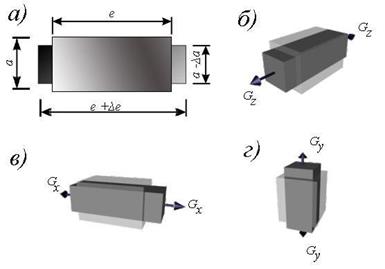
Рис. 1.16. Деформация элемента при растяжении:
а) общий вид элемента; б) деформации в направлении осиz;
в) то же оси x; г) то же оси у
Системы, для которых соблюдается условие пропорциональности между напряжениями и деформациями, подчиняютсяпринципу суперпозиции, или принципунезависимости действия сил.
В соответствии с этим принципом перемещения и внутренние силы, возникающие в упругом теле, считаются независящими от порядка приложения внешних сил. То есть, если к системе приложено несколько сил, то можно определить внутренние силы, напряжения, перемещения и деформации от каждой силы в отдельности, а затем результат действия всех сил получить как сумму действий каждой силы в отдельности. Принцип независимости действия сил является одним из основных способов при решении большинства задач механики линейных систем.