Файл: Учебное пособие по дисциплине Механика Модуль Прикладная механика.docx

С понятием однородности тесно связано понятие сплошности среды, под которым подразумевают тот факт, что материал конструкции полностью заполняет весь отведенный ему объем, а значит в теле конструкции нет пустот и не учитывается реальная структура материала (зернистая, кристаллическая и др.). Это допущение позволяет использовать в сопротивлении материалов методы математического анализа (дифференциальное и интегральное исчисления). Для большинства машиностроительных конструкций расчеты, основанные на допущении о сплошности строения дают 

практически удовлетворительные результаты. Это объясняется тем, что размеры детали во много раз больше межатомных расстояний.

2. Обычно сплошная среда принимается изотропной, т.е. предполагается, что свойства тела, выделенного из нее, не зависят от его ориентации в пределах этой среды. Материалы, имеющие различные свойства в разных направлениях, называют анизотропными (например, дерево, ткани (косой и кривой крой), армированная пластмасса, бетон). К анизотропным относятся и материалы с направленной кристаллизацией и с монокристаллической структурой. Отдельно взятый кристалл материала анизотропен, но т.к. в объеме реального тела содержится бесконечно большое количество хаотично расположенных кристаллов, принимается, что материал изотропен.

Металлы и сплавы, как правило, изотропны, так как большинство металлов имеет мелкозернистую структуру. Благодаря большому количеству кристаллов свойства материалов выравниваются в различных направлениях и можно считать эти материалы практически изотропными. В настоящее время широкое распространение получили анизотропные композиционные материалы, состоящие из двух компонентов – наполнителя и связующего. Наполнитель состоит из уложенных в определенном порядке высокопрочных нитей – матрицы, что и определяет значительную анизотропию композита. Композиционные материалы имеют высокую прочность при значительно меньшем, чем металлы весе. 

3. Принимается, что до определенной величины деформации материалов подчиняются закону Гука и весьма малы относительно размеров тела, поэтому все расчеты выполняются по исходной, т.е. недеформированной, схеме, к которой применим принцип независимости действия сил (принцип суперпозиции).

Результат воздействия на тело системы сил равен сумме результатов воздействия тех же сил, прилагаемых к телу последовательно и в любом порядке (рис. 1.9). Под словами «результат воздействия» следует понимать – деформации, внутренние силы и перемещения отдельных точек.

---

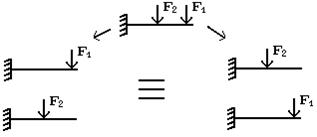
Рис. 19. Использование принципа суперпозиции
Должны соблюдаться два условия:

1. перемещения малы по сравнению с размерами тела,

2. перемещения линейно зависят от силы.

С помощью этого принципа сложный случай приводится к простым.

4. После снятия нагрузки геометрические размеры тела полностью или частично восстанавливаются. Свойство тела восстанавливать свои первоначальные размеры после разгрузки называется упругостью. При решении большинства задач в сопротивлении материалов принимается, что материал конструк­цийабсолютно упругий. Это допущение справедливо, пока нагрузки не превышают определенного значения. При больших нагрузках в элементах конструкций появляются пластические деформации. Пластичностьюназывается свойство тела сохранять после прекращения действия нагрузки, или частично полученную при нагружении, деформацию.

Ползучестьюназывается свойство тела увеличивать деформацию при постоянных внешних нагрузках.

5. Перемещения, возникающие под действием внешних сил в упругом теле, малы по сравнению с его размерами. Это допущение называетсяпринципом начальных размеров. В большинстве случаев механические конструкции работают в упругой зоне (в зоне действия закона Гука), а упругие деформации малы по сравнению с геометрическими размерами (рис. 1.10). Допущение позволяет при составлении уравнений равновесия пренебречь изменениями формы и размеров конструкции. 



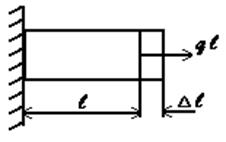
∆l≪l

Рис. 1.10. Принцип неизменности геометрических размеров

 

6. Предполагается, что в сечениях, достаточно удаленных от мест приложения нагрузки, характер распределения напряжений не зависит от конкретного способа нагружения.  Основанием для такого утверждения служит принцип Сен-Венана, справедливый для любого типа напря­женного состояния и формулируемый следующим образом: особенности приложения внешних нагрузок проявляются, как правило, на расстояниях, не превышающих характерных размеров поперечного сечения стержня или другое определение: в точках тела, достаточно удаленных от мест приложения нагрузок, величина внутренних сил весьма мало зависит от конкретного способа приложения этих нагрузок, а зависит только от ее статического эквивалента

---

 (рис. 11). Этот принцип во многих случаях позволяет производить замену одной системы сил другой системой, статически эквивалентной, что позволяет часто значительно упростить расчет.



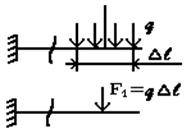
Рис. 1. 11. Использование принципа Сен-Венана
7. Принимается гипотеза плоских сечений(гипотеза Бернулли), 

введенной швейцарским ученым Д. Бернулли, гласящей, что плоские поперечные сечения стержня до деформации остаются плоскими и после деформации (рис.12).



Рис. 1.12. Гипотеза плоских  сечений

 

8. Считается, что ненагруженное тело свободно от каких бы то ни было внутренних сил любой природы. Изменению формы и размеров тела под нагрузкой сопротивляются силы взаимодействия между частицами материала, называемые силами упругости. В дальнейшем, говоря о внутренних силах, будем иметь в виду именно эти силы упругости, не принимая во внимание молекулярные силы, имеющиеся и в ненагруженном теле. Это допущение полностью не выполняется ни для одного материала. Причины возникновения неравномерных внутренних или начальных усилий:

- В стальных деталях из-за неравномерного остывания;

- В дереве из-за неравномерного высыхания;

- В бетоне в процессе твердения.

В тех случаях, когда есть основания предполагать, что эти силы значительны, стараются определить их экспериментально. Однако, часто они достаточно малы, чтобы их учитывать.

 Использование этих понятий и допущений существенно упрощает изучение поведения конструкций под нагрузкой, а соответствие условного материала реальным материалам достигается введением в расчет элементов сооружений экспериментально получаемых механических характеристик реальных материалов. 

3. 
   Напряжения
   

При определении внутренних силовых факторов их считают приложенными в центре тяжести сечения. В действительности внутренние силы, являясь результатом взаимодействия частиц тела, непрерывно распределены по сечению. Интенсивность этих сил в разных точках сечения может быть различной. При увеличении нагрузки на элемент конструкции увеличиваются внутренние силы и соответственно увеличивается их интенсивность во всех точках сечения. Если в некоторой точке интенсивность внутренних сил достигнет определенного для данного материала значения, в этой точке возникает трещина, развитие которой приведет к разрушению элемента, или возникнут недопустимые пластические деформации. Следовательно, о прочности элементов конструкций следует судить не по

---

значению внутренних силовых факторов, а по их интенсивности. Меру интенсивности внутренних сил называют напряжением.

В окрестности произвольной точки, принадлежащей сечению некоторого нагруженного тела, выделим элементарную площадку  , в пределах которой действует внутреннее усилие ∆F (рис. 1.13, а).

Среднее значение интенсивности внутренних усилий на площадке, называемое средним напряжением, определяют по формуле



Уменьшая площадь ∆A, в пределе получаем истинное напряжение в данной точке сечения



Векторная величина p называется полным напряжением в точке. В международной системе единиц (СИ) за единицу напряжения принят паскаль (Па=Н/м²) – это напряжение, при котором на площадке 1 м² действует внутренняя сила 1 Н.

Так как эта единица очень мала, в расчетах используют кратную единицу напряжения – мегапаскаль (1 МПа=10⁶ Па).

Разложим вектор полного напряжения p на две составляющие (рис.1.13, б).

Проекция вектора полного напряжения p на нормаль к данной площадке обозначается через σ и называется нормальным напряжением.



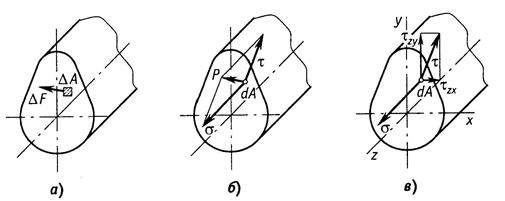
Рис. 1.13

 

Составляющую, лежащую в сечении в данной площадке обозначается через τ и называется касательным напряжением.

Нормальное напряжение, направленное от сечения, считают положительным, направленное к сечению – отрицательным.

Нормальные напряжения возникают, когда под действием внешних сил частицы, расположенные по обе стороны от сечения, стремятся удалиться одна от другой или сблизиться. Касательные напряжения возникают, когда частицы стремятся сдвинуться одна относительно другой в плоскости сечения.

Касательное напряжение можно разложить по координатным осям на две составляющие   и   (рис.1.13, в). Первый индекс при τ показывает, какая ось перпендикулярна сечению, второй – параллельно какой оси действует напряжение. Если в расчетах направление касательного напряжения не имеет значения, его обозначают без индексов. 

---

Между полным напряжением и его составляющими существует зависимость



Через точку тела можно провести бесконечное число сечений и для каждого из них напряжения имеют свое значение. Следовательно, при определении напряжений необходимо указывать положение не только точки тела, но и сечения, проведенного через эту точку.

Совокупность напряжений для множества элементарных площадок, проходящих через данную точку, образует напряженное состояние в этой точке.

В дифференциальные уравнения равновесия бесконечно малого прямоугольного параллелепипеда входят шесть независимых скалярных величин, соответствующих составляющим напряжений по его граням. Они определяют тензор напряжений:



При этом учитывается свойство парности касательных напряжений (τ_xy = τ_yx,  τ_xz = τ_zx,  τ_yz= τ_zy): на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к линии пересечения площадок, равны по величине и взаимно направлены либо к линии пересечения, либо от нее.

Если площадка dA совпадает с поверхностью тела, то составляющие напряжения трансформируются в составляющие внешних сил, действующих на поверхности тела. Соответствующие уравнения выражают условия на поверхности, или статические граничные условия.

Площадка, на которой касательные напряжения равны нулю, называется главной. Через точку проходят три главные площадки. По ним действуют главные напряжения, которые обозначаются σ₁, σ₂, σ₃ (σ_1≥σ₂ ≥σ₃).

Напряжения в поперечных сечениях связаны с внутренними силовыми факторами определенными зависимостями.

Возьмем в сечении бесконечно малую площадку площадью dA. По этой площадке в общем случае действуют бесконечно малые (элементарные) внутренние силы (рис. 1.14)

---