Файл: Е. В. Буцко А. Г. Мерзляк В. Б. Полонский М. С. Якир.docx

601. Не могла. Два последовательных натуральных числа, записанных на сто- ронах одной страницы, имеют разную чётность, а значит, их сумма — число нечётное. Тогда понятно, что сумма 35 нечётных чисел не может быть равной числу 3 500.




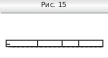
632. Можно. Надо расположить ряды бе- лых и чёрных палочек друг под другом (рис. 15) и распиливать «чёрный» ряд напротив стыков белых палочек и на- оборот.

660. Утверждение станет очевидным, если представить себе, что движение проис-

ходит не в разные дни, а «раздвоившийся» турист в один и тот же день шёл навстречу «сам себе».

679. 17. Серёжа зачёркивал последнюю цифру в числе вида 32b . Так как это число должно быть кратным 19, то b = 3. Тогда Андрей задумал число 17 = 323 : 19.

698. 16. В первые шесть минут будут записаны соответственно числа 18, 20,

12, 14, 16, 18. Теперь понятно, что полученная последовательность яв- ляется периодической с периодом, равным 5, и её шестидесятый член равен пятому.

730. Не могло. Из условия следует, что количество грибов, собранных каж- дой парой, кратно 3. Значит, числу 3 кратно и общее количество всех собранных детьми грибов.

766. Существует. Такой магический квадрат можно получить, поделив все числа данного магического квадрата на их наименьшее общее кратное.

783. Не может. Предположим, что такие числа существуют. Обозначим их a и b, где a < b. Тогда существует натуральное число n > 1 такое, что b= na. Заметим, что при n> 3 имеем na≥ 4 ⋅ 1 234, которое боль- ше b. Если n = 3, то получаем, что число b кратно 3, а это не так. Остаётся заметить, что при n = 2 запись числа 2а содержит цифры

6 и 8.

801. 132 дня. Для того чтобы любое из пары данных чисел могло означать как номер месяца, так и номер дня, каждое из них должно быть нату- ральным и не превышать 12. Таких пар 144. Кроме того, если пара со- стоит из равных чисел, то записанная дата определяется однозначно. Пар с равными компонентами — 12. Таким образом, определить дату

---

невозможно только в 144 − 12 = 132 случаях.

829. Не может. Если предположить, что в сетке 999 узлов, то количество от- резков верёвки, соединяющих соседние узлы, должно быть равным999 3 _.

2

845. Могут. Мальчики должны поплыть на другой берег. Один из них остаёт- ся там, а второй возвращается. Один турист переправляется, а мальчик, остававшийся на другом берегу, возвращает лодку, и все повторяется.

870. Нельзя. Следует заметить, что количество стаканов, стоящих вверх дном, изменяется на чётное число (на 2, 4 или 0), а поскольку первона- чальное количество таких стаканов 7, то их количество будет оставать- ся нечётным числом.

893. Сможет. Одну дозу нужных лекарств можно получить, если взять по од- ной половинке каждой из шести имеющихся таблеток.

918. Суббота. Апрель. Из условия следует, что в этом месяце 30 дней, а вос- кресенье и понедельник — два последних дня этого месяца.

951. 35 распилов. Заметим, что количество четырёхметровых брёвен крат- но 5. Тогда возможны два случая: 1) количество четырёхметровых брё- вен равно 10, а пятиметровых — 1; 2) количество тех и других брёвен равно 5. Теперь можно подсчитать, что в первом случае понадобится 34 распила, а во втором — 35.

975. Пусть Б_i и Ч_i — количество партий, которые выиграл i-й участник, играя белыми и чёрными фигурами соответственно, S_ч — количество партий турнира, в которых победу одержали чёрные фигуры. Тогда из условия следует, что Б_i = S_ч – Ч_i или Б_i + Ч_i = S_ч. Теперь видим, что в ле- вой части полученного равенства записано общее количество побед,

завоёванных i-м участником, а справа — константа для этого турнира.

992. Сможет. Длина по крайней мере

---

одного из двух получившихся кусков больше 12 м. От этого куска можно отрезать нужный кусок длиной в 12 м. После этого останутся два куска, суммарная длина которых равна 13 м. Следовательно, длина по крайней мере одного из них больше 6 м. Отре- зав нужный кусок длиной 6 м, вновь получим два куска. Далее, рассуждая аналогично, приходим к выводу, что можно последовательно получить куски, длины которых соответственно равны 3 м, 2 м, 1 м.

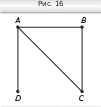1023. Пусть A — один из шести человек. Тогда


Dнезнакомы с A.
среди остальных пяти найдутся по край- ней мере либо трое с ним знакомых, ли- бо трое с ним незнакомых. Пусть B, C, D знакомы с A (рис. 16). Если среди них найдутся знакомые друг с другом (напри- мер, B и C), то вместе с A они образуют тройку попарно знакомых. Если же B, C и Dмежду собой незнакомы, то они сами образуют нужную тройку. Аналогично можно рассмотреть случай, когда B, C и

1054. Сначала рассмотрим случай, когда каждая из команд сыграла хотя бы один матч. Тогда количество матчей, сыгранных любой из команд, принадлежит множеству {1, 2, ..., 15}. Так как команд 16, то по принци- пу Дирихле найдутся две команды, сыгравшие поровну матчей.

Если среди участников есть команда, не сыгравшая ни одного матча, то нет команды, которая сыграла бы все 15 матчей. В этом случае количе- ство матчей, сыгранных любой командой, — элемент множества {0, 1, 2, ..., 14}. Теперь снова

---

можно использовать принцип Дирихле.

1074. В пяти видах. Пусть n— количество видов спорта, а m— общее количе- ство баллов, которые присуждаются в розыгрыше одного вида (m≥ 1 + 2 +

+ 3 + 4 = 10). Тогда m ⋅ n = 16 + 14 + 13 + 12 = 55 = 11 ⋅ 5.

1114. Таким свойством обладает наименьшее из данных восьми чисел.

1142. Предположим, что из A нельзя проехать в B. Пусть A₁, A₂, A₃ — горо- да, соединённые дорогой с A, а B₁, B₂, B₃ — города, соединённые доро- гой с B, причём все указанные города разные. Но тогда в стране не ме-

нее 8 городов.

1172. Нельзя. Каждая косточка домино покрывает одну белую и одну чёрную клеточку. Значит, фигура, которую можно покрыть косточками, долж- на содержать равное количество чёрных и белых клеточек.

1218. Существуют. Например, a₁ = a₂ = … = a₁₀₀₃ = 1, a₁₀₀₄ = 2, a₁₀₀₅ = 1005.

1243. Не может. Общее число чистых и запачканных клеток — число чётное.

Следовательно, и разность этих чисел должна быть чётным числом.

1279. Если в некоторый момент отмечено n точек, то после очередного вы- полнения описанной операции будет отмечено 2n − 1 точка.

1295. Достаточно задать такой вопрос: «Вы житель этого города?». Тогда от- рицательный ответ будет означать, что путешественник находится в городе лжецов, утвердительный — что он в городе правдивых людей.

1334. Выиграет первый игрок. Для этого ему достаточно первым своим хо- дом «выровнять» кучки, взяв из большей один камешек, а потом при- держиваться симметричной стратегии, то есть если второй игрок возьмёт некоторое количество камешков из одной кучки, то первому следует взять такое же количество из другой.

1346. Не могут. Каждая из указанных сумм может принимать одно из 13 зна- чений: −6, −5, −4, ..., 5, 6. Всего же сумм есть 14.

---

Тогда по принципу Ди-

рихле найдутся две равные суммы.

Содержание

Примерное тематическое планирование 3

Организация учебной деятельности 8

Глава 1. Делимость натуральных чисел 8

Глава 2. Обыкновенные дроби 33

Глава 3. Отношения и пропорции 87

Глава 4. Рациональные числа и действия над ними 126

Методические рекомендации по оценке

образовательных достижений учащихся 221

Методические рекомендации по формированию

ИКТ-компетентности учащихся 223

Методические рекомендации по организации учебно-исследовательской и проектной

деятельности учащихся 226

Математические диктанты 231

Контрольные работы 253

Решения задач рубрики «Задача от мудрой совы» 282
Учебно-методическое пособие
Буцко Елена Владимировна Мерзляк Аркадий Григорьевич Полонский Виталий Борисович Якир Михаил Семёнович

Математика

6 класс

Методическое пособие
Редактор Э.А. Мазурова

Внешнее оформление К.В. Бычкова Художественный редактор М.В. Новоторцев Компьютерная вёрстка А.А. Исаковой Технический редактор Л.Е. Пухова Корректоры А.С. Цибулина, Е.В. Плеханова
Подписано в печать 30.12.15. Формат 70×90/16 Гарнитура NewBaskerville. Печать офсетная Бумага офсетная № 1. Печ. л. 18,0

Тираж 2000 экз. Заказ №

ООО Издательский центр «Вентана-Граф» 127422, Москва, ул. Тимирязевская, д. 1, стр. 3

Тел./факс: (495) 611-15-74, 611-21-56

E-mail: info@vgf.ru, http://www.vgf.ru

---