Файл: Е. В. Буцко А. Г. Мерзляк В. Б. Полонский М. С. Якир.docx

ведите отрезок CD.

1. 
   Найдите координаты точки пересечения отрезка CD с осью орди- нат.
   
2. 
   Постройте отрезок, симметричный отрезку CD относительно оси абсцисс, и найдите координаты концов полученного отрезка.
   
1. 
   Начертите тупой угол OCA, отметьте на его стороне CA точку P. Про- ведите через точку P прямую, перпендикулярную прямой CA, и пря- мую, перпендикулярную прямой CO.
   
2. 
   Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 6 изображён график движения велосипедиста.
   

Рис. 6
s, км
32
24
16
8
0	2	4	6	8	10	12	14	t, ч

1. 
   На каком расстоянии от дома был велосипедист через 4 ч после на- чала движения?
   
2. 
   Сколько времени велосипедист затратил на остановку?
   
3. 
   Через сколько часов после начала движения велосипедист был на расстоянии 24 км от дома?
   
4. 
   С какой скоростью ехал велосипедист до остановки?
   
1. 
   Даны координаты трёх вершин прямоугольника ABCD: A (−1; −3),
   

---

C (5; 1) и D (5; −3).

1. 
   Начертите этот прямоугольник.
   
2. 
   Найдите координаты вершины B.
   
3. 
   Найдите координаты точки пересечения диагоналей прямоуголь- ника.
   
4. 
   Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
   
1. 
   Изобразите на координатной плоскости все точки (x; y) такие, что
   

y = −4, x — произвольное число.

Вариант 3

1. 
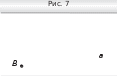   Перерисуйте в тетрадь рисунок 7. Проведите через точку B:
   
   1. 
      прямую b, параллельную прямой a;
      
   2. 
      прямую c, перпендикулярную пря- мой a.
      
2. 
   Начертите произвольный треуголь- ник MKP. Постройте фигуру, симме- тричную этому треугольнику относи- тельно точки P.
   
3. 
   Отметьте на координатной плоскости точки М(1; 2) и N(−1; 6). Про-
   

ведите отрезок MN.

1. 
   Найдите координаты точки пересечения отрезка MN с осью орди- нат.
   
2. 
   Постройте отрезок, симметричный отрезку MN относительно оси абсцисс, и найдите координаты концов полученного отрезка.
   
1. 
   Начертите тупой угол MCK, отметьте на его стороне CM точку A. Проведите через точку A прямую, перпендикулярную прямой CM, и прямую, перпендикулярную прямой CK.
   
2. 
   Велосипедист выехал из дома и через некоторое время вернулся назад. На рисунке 8 изображён график движения велосипедиста.
   
   1. 
      На каком расстоянии от дома был велосипедист через 3 ч после на- чала движения?
      
   2. 
      Сколько времени велосипедист затратил на остановку?
      
   3. 
      Через сколько часов после начала движения велосипедист был на расстоянии 30 км от дома?
      

      Рис. 8
      s, км
      40
      30
      20
      10
      0	2	4	6	8	10	12 t, ч

   4. 
      С какой скоростью ехал велосипедист до остановки?
      
3. 
   Даны координаты трёх вершин прямоугольника ABCD: A (−2; −2),
   

---

B (−2; 4) и D (6; −2).

1. 
   Начертите этот прямоугольник.
   
2. 
   Найдите координаты вершины C.
   
3. 
   Найдите координаты точки пересечения диагоналей прямоуголь- ника.
   
4. 
   Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
   
1. 
   Изобразите на координатной плоскости все точки (x; y) такие, что
   

x = −4, y — произвольное число.

Вариант 4

1. 
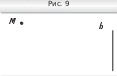   Перерисуйте в тетрадь рисунок 9. Проведите через точку M:
   
   1. 
      
      c
      прямую a, параллельную прямой b;
      
   2. 
      прямую , перпендикулярную пря- мой b.
      
2. 
   Начертите произвольный треуголь- ник ADK. Постройте фигуру, симме- тричную этому треугольнику относи- тельно точки D.
   
3. 
   Отметьте на координатной плоскости точки K(1; −1) и M(4; 2). Про-
   

ведите отрезок KM.

1. 
   Найдите координаты точки пересечения отрезка KM с осью аб- сцисс.
   
2. 
   Постройте отрезок, симметричный отрезку KMотносительно оси
   

ординат, и найдите координаты концов полученного отрезка.

4. 
   Начертите тупой угол APR, отметьте на его стороне PR точку E. Про- ведите через точку E прямую, перпендикулярную прямой PR, и пря- мую, перпендикулярную прямой AP.
   
5. 
   Турист вышел из базового лагеря и через некоторое время вернулся назад. На рисунке 10 изображён график движения туриста.
   

Рис. 10
s, км
10
8
6
4
2
0	2	4	6	8	10 t, ч

---

1. 
   На каком расстоянии от лагеря был турист через 2 ч после начала движения?
   
2. 
   Сколько времени турист затратил на остановку?
   
3. 
   Через сколько часов после начала движения турист был на расстоя- нии 5 км от лагеря?
   
4. 
   С какой скоростью шёл турист до остановки?
   
1. 
   Даны координаты трёх вершин прямоугольника ABCD: B(−3; 6);
   

C (5; 6) и D (5; −2).

1. 
   Начертите этот прямоугольник.
   
2. 
   Найдите координаты вершины A.
   
3. 
   Найдите координаты точки пересечения диагоналей прямоуголь- ника.
   
4. 
   Вычислите площадь и периметр прямоугольника, считая, что длина единичного отрезка координатных осей равна 1 см.
   
1. 
   Изобразите на координатной плоскости все точки (x; y) такие, что
   

y = 3, x — произвольное число.

Контрольная работа № 12

Повторение и систематизация знаний учащихся

Вариант 1

1. 
   Найдите значение выражения:
   

1) (12,4  8,9)  1 ³ ; 2) ^⎛_⎜ 2 ³  1 ^{5 ⎞}_⎟ : ^⎛_⎜ 1 ^{5 ⎞}_⎟ .

7 _⎝ 8 6 _{⎠ ⎝} 8 _{⎠ 8}

2. 
   В 6 А классе 36 учеников. Количество учеников 6 Б класса составляет ₉ количества учеников 6 А класса и 80 % количества учеников 6 В класса. Сколько человек учится в 6 Б классе и сколько — в 6 В классе?
   
3. 
   Отметьте на координатной плоскости точки A(−3; 1), B(0; −4) и
   

M(2; −1). Проведите прямую AB. Через точку Mпроведите прямую

---

a,

параллельную прямой AB, и прямую b, перпендикулярную прямой AB.

4. 
   В первом ящике было в 4 раза больше яблок, чем во втором. Когда из первого ящика взяли 10 кг яблок, а во второй положили ещё 8 кг, то в обоих ящиках яблок стало поровну. Сколько килограммов яблок было в каждом ящике вначале?
   
5. 
   Решите уравнение:
   

8x − 3(2x + 1) = 2x + 4.

Вариант 2

1. 
   Найдите значение выражения:
   

1) (0,76  0,44) : 2 ² ; 2) ^⎛_⎜ 3⁵  2 ^{3 ⎞}_⎟  ^⎛_⎜ 3^{5 ⎞}_⎟ .

го — 4 пассажира, то в обоих вагонах пассажиров стало поровну. Сколь- ко пассажиров было в каждом вагоне вначале?

5. 
   Решите уравнение:
   

10x − 2(4x − 5) = 2x + 10.

Вариант 3

1. 
   Найдите значение выражения:
   

1) (4,3  1,2) : ^⎛_⎜

---