Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx

х не зависит от значения х.

4. Найдите значение выражения:

+

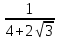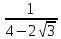
5.Расположите в порядке возрастания числа: 3,1; ; ; ; .

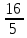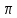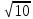Критерии оценки:

«5» - ставится за 5 верно решенных заданий;

«4» - ставится за 4 верно решенных задания;

«3» - ставится за 3 верно решенных задания;

«2» - если решено менее 3 заданий.

Литература.

Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.

Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 1.1. Развитие понятия о числе.
Практическая работа №2
Решение задач на выполнение действий с приближенными числами
Цель: закрепить полученные знания по теме в процессе решения задач.

Абсолютной погрешностью приближения называется модуль разности между истинным значением величины и её приближённым значением. , где — истинное значение, — приближённое.

Относительной погрешностью приближения называется отношение абсолютной погрешности к модулю приближённого значения величины.

, где — истинное значение, — приближённое.

Относительную погрешность обычно вызывают в процентах.

Пример. При округлении числа до единиц получается число .

Относительная погрешность равна . Говорят, что относительная погрешность в этом случае равна .
Важнейшей задачей приближённых вычислений помимо нахождения приближённого значения величины является оценка абсолютной или относительной погрешности.

Например, число 3, 14 является приближённым значением числа , при этом абсолютная погрешность не превосходит .
Задания к практической части.

1. Записать числа в виде двойного неравенства.

а0=547,06, Δа=0,005	а0=0,5478 , Δа=0,0001
а0=8,4589 , Δа=0,0001	а0=21457 , Δа=50
а0=457000 , Δа=200	а0= 5,4782, Δа=0,124
а0=0,1245 , Δа=0,0002	а0=44,558 , Δа=0,24

---

2. Округлить с точностью до 0,01 следующие числа.

0,4558	3,54628	6,54987
15,254	26,4782	3,54628
11,6987	64,2498	2,5487
13,89214	3,9987	9,01124
25,3698	6548,1254	45,6982

3. Найти границу относительной погрешности числа а.

а=6,96 , Δа=0,02	а= 12,79, Δа=2
а= 648,5, Δа=0,05	а= 792,3, Δа=0,05
а=2,372 , Δа=0,004	а=4,25 , Δа=0,02
а=34,27 , Δа=0,005	а= 1,9345, Δа=0,0005

Критерии оценки:

Процент результативности (правильных ответов)	Качественная оценка индивидуальных образовательных достижений
	балл (отметка)	вербальный аналог
90 ÷ 100	5	отлично
80 ÷ 89	4	хорошо
70 ÷ 79	3	удовлетворительно
менее 70	2	не удовлетворительно

Литература:

Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.

Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 1.2. Корни, степени и логарифмы

Практическая работа №3

Вычисление и сравнение корней.

Цель: закрепить полученные знания по теме в процессе решения задач.

Вычисление и сравнение корней. Свойства корней степени n: если 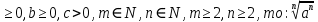a = a ; ; ; ;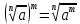

---

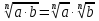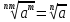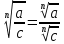
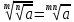
Пример: 1) Вычислите: 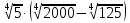= = 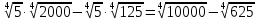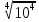- 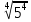= 10 - 5 = 5

Задания к практической части.

	Вариант 1	Вариант 2
1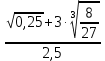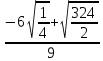
2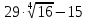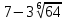
3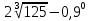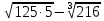
4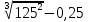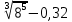
5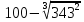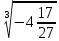
6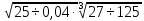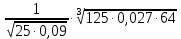
7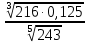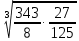
8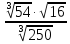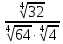
9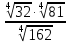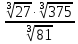
10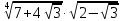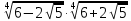

---

Критерии оценки:

«5» - ставится за 5 верно решенных заданий;

«4» - ставится за 4 верно решенных задания;

«3» - ставится за 3 верно решенных задания;

«2» - если решено менее 3 заданий.

Литература.

Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.

Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 1.2. Корни, степени и логарифмы

Практическая работа №4

Решение задач на свойства степени

Цель: способствовать закреплению навыков работы со степенями с рациональными показателями.
Свойства степени с рациональным показателем.

1. 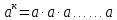( к раз)

2.

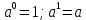
3.

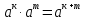
4. =

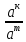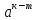
5. =

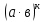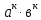
6. =

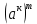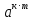
7. =
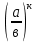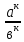
Примеры.

1.

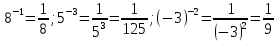
2. = = =

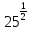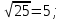
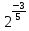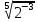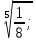
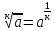
3. ;

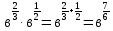4. = = = = =

---

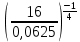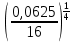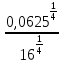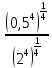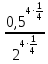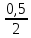
= 0.25

5. = = = =
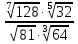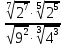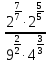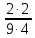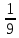
Задания к практической работе.

Вариант 1	Вариант 2
1. 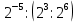2. 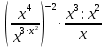3. 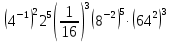4. 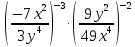5. 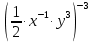:	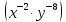1. 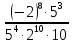2. 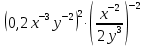3. 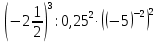4. 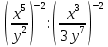5.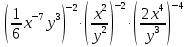

Критерии оценки:

«5» - ставится за 5 верно решенных заданий;

«4» - ставится за 4 верно решенных задания;

«3» - ставится за 3 верно решенных задания;

«2» - если решено менее 3 заданий.

Литература.


Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.

Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.

---