Файл: Методические рекомендации для обучающихся к выполнению практических работ по учебной дисциплине.docx
Добавлен: 12.01.2024
Просмотров: 203
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Критерии оценки:
«5» - ставится за 9-10 верно выполненных заданий;
«4» - ставится за 7-8 верно выполненных задания;
«3» - за 5-6 верно выполненных задания;
«2» - за менее 5 заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Тема 1.2. Корни, степени и логарифмы
Практическая работа № 9
Решение логарифмических уравнений и неравенств.
Цель: закрепление знаний, отработка навыков решения логарифмических уравнений и неравенств.
Пояснения к работе:
Определение: Логарифмом положительного числа b по основанию a () называется показатель степени, в которую надо возвести a, чтобы получить b.
 .
.Свойства логарифмов.
 ;
;  ;
;  (a
(a ). Основное логарифмическое тождество:
). Основное логарифмическое тождество: 
Примеры. 1) Решите уравнение:
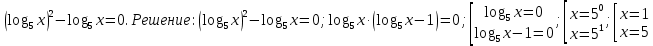 ответ: 1;5
ответ: 1;52) Решите неравенство:
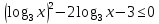 Решение: Обозначив
Решение: Обозначив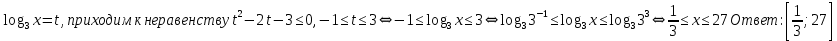
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Решите уравнение: а) 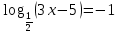 б) 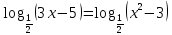 в) 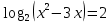 г) 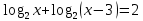 д) 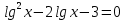 2. Решите неравенство: а) 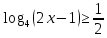 б) 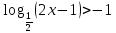 в) 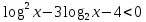 г) 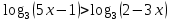 3. Решите систему уравнений: 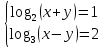 | 1. Решите уравнение: а) 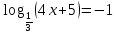 б) 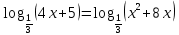 в) 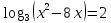 г) 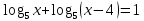 д) 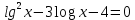 2. Решите неравенство: а) 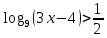 б) 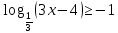 в) 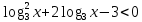 г) 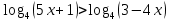 3. Решите систему уравнений: 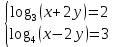 |
Критерии оценки: «5» - ставится за 9-10 верно выполненных заданий;
«4» - ставится за 7-8 верно выполненных заданий;
«3» - за 5-6 верно выполненных заданий;
«2» - менее пяти заданий.
Литература.
Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
Раздел 2. ГЕОМЕТРИЯ
Тема 2.1. Прямые и плоскости в пространстве.
Практическая работа № 10
Параллельность прямых и плоскостей
Цель: закрепление знаний, отработка навыков применения параллельности прямых и плоскостей при решении задач.
Пояснения к работе:
Определение 1. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек
Определение 2. Прямая и плоскость в пространстве называются параллельными, если они
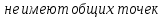 .
.Определение 3. Две плоскости называются параллельными, если они
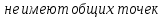 .
.Пример: Концы данного отрезка длиной 125 см отстоят от плоскости на 100 см и 56 см. Найти длину его проекции.
 | Решение: Искомая длина проекции равна двум параллельным сторонам прямоугольника и одновременно нижнему катету прямоугольного треугольника. Из прямоугольного треугольника по теореме Пифагора найдём этот катет. 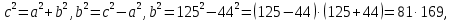 (второй катет равен 100 - 56 = 44 ).b = (второй катет равен 100 - 56 = 44 ).b = 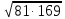 = 9 = 9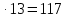 см. Ответ: 117 см см. Ответ: 117 см |
Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Сделать схематический А 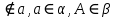 | рисунок: а 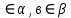 |
| 2.Каким может быть взаимное расположение прямых в пространстве? Дать соответствующие определения и обозначения, прямой и плоскости в пространстве показать на чертежах. | |
| 3. Через сторону правильного шестиугольника проведена плоскость. Указать положение других сторон шестиугольника относительно плоскости. | 3. Сколько пар скрещивающихся ребер имеется в треугольной пирамиде АВСД ? |
| 4. Построить прямую, параллельную двум данным плоскостям. | 4.Прямая 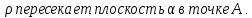 Существует ли плоскость, проходящая через прямую 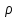 и параллельная плоскости и параллельная плоскости 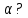 |
| 5. Каким может быть взаимное расположение плоскостей 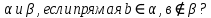 | 5. На чертеже куба указать пары параллельных и пересекающихся плоскостей. |
| 6. Концы данного отрезка длиной 125 см отстоят от плоскости на 100 см и 56 см. Найти длину его проекции. | |
| 7. Параллельные прямые АВ и СД лежат в плоскости М на расстоянии 28 см одна от другой; ЕК – внешняя прямая, параллельная АВ и удаленная от АВ на 17 см, а от плоскости М на 15 см. Найти расстояние между ЕК и СД. | |
| 8. Расстояние между двумя параллельными плоскостями равно 8 дм. Отрезок длиной 10 дм своими концами упирается в эти плоскости. Определить проекции отрезка на каждую плоскость. | |
Критерии оценки:
«5» ставится за 8 верно решенных заданий;
«4» ставится за 6-7 верно решенных заданий;
«3» ставится за 4-5 верно решенных задания;
«2» - если решено менее 4 заданий.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
Тема 2.1. Прямые и плоскости в пространстве
Практическая работа № 11
Перпендикулярность прямых и плоскостей
Цель работы: закрепление знаний, отработка навыков применения перпендикулярности прямых и плоскостей при решении задач.
Пояснения к работе: Определение 1. Две прямые в пространстве называются перпендикулярными
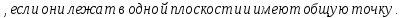 Определение 2. Прямая в пространстве называется перпендикулярной плоскости
Определение 2. Прямая в пространстве называется перпендикулярной плоскости
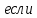 она перпендикулярна любой прямой
она перпендикулярна любой прямой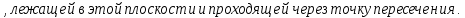 Определение 3. Две плоскости называются перпендикулярными, если третья плоскость, проведенная
Определение 3. Две плоскости называются перпендикулярными, если третья плоскость, проведенная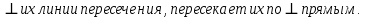
Пример: Из данной точки проведены к данной плоскости две наклонные, равные каждая 2 см; угол между ними равен 60
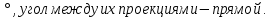 Найти расстояние данной точки от плоскости. Решение. Треугольник, в который входят обе наклонные - равносторонний, все углы равны по 60
Найти расстояние данной точки от плоскости. Решение. Треугольник, в который входят обе наклонные - равносторонний, все углы равны по 60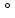 , все стороны равны по 2 см. Но если равны наклонные, то равны и их проекции. Тогда из треугольника, лежащего в плоскости, по теореме Пифагора находим его катеты:
, все стороны равны по 2 см. Но если равны наклонные, то равны и их проекции. Тогда из треугольника, лежащего в плоскости, по теореме Пифагора находим его катеты: 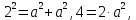
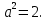 Из треугольника ( перпендикуляр – наклонная – проекция) находим перпендикуляр:
Из треугольника ( перпендикуляр – наклонная – проекция) находим перпендикуляр: 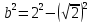 ,
, 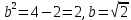 .
.Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Дано: MN 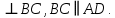 Будет ли прямая MN Будет ли прямая MN 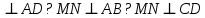 ? ? | 1. Дано: AO 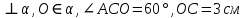 . Найти: . Найти: 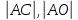 |
| 2. Дано: точка B, прямая с, В 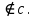 Провести через точку В плоскость Провести через точку В плоскость 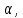 перпендикулярную прямой с. перпендикулярную прямой с. | 2. Дано: АВСД 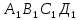 - куб. Доказать, что ВД - куб. Доказать, что ВД 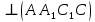 . . |
| 3. Дано: АВ 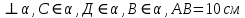 , , 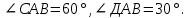 Найти: Найти: 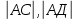 | 3. Дано: АВ 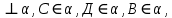 АВ = 20 см, АВ = 20 см, 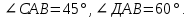 Найти: Найти: 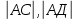 |
| 4. Из некоторой точки, находящейся на расстоянии 6 см от плоскости, проведена к ней наклонная, равная 10 см. Найдите ее проекцию на данную плоскость. | 4. Из некоторой точки проведены к данной плоскости перпендикуляр, длина которого равна 5 см и наклонная. Угол между ними равен 45 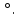 Найдите длину наклонной. Найдите длину наклонной. |
| 5. Из некоторой точки пространства проведены к плоскости две наклонные длиной 20 см и 15 см, длина проекции первой наклонной на плоскость равна 16 см. Найдите длину проекции второй наклонной. | 5. Из данной точки проведены к данной плоскости две наклонные, равные каждая 2 см. Угол между ними равен 60 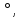 а угол между их проекциями - прямой. Найдите расстояние от данной точки до плоскости. а угол между их проекциями - прямой. Найдите расстояние от данной точки до плоскости. |
| 6. Провести плоскость, проходящую через концы трех ребер куба, выходящих из одной вершины. Ребро куба равно 2. Вычислить площадь сечения. | 6. Ребра прямоугольного параллелепипеда равны 3 см, 4 см и 7 см. Определить площадь сечения, проведенного через концы трех ребер, выходящих из одной вершины. |
Критерии оценки: «5» ставится за 6 верно решенных заданий;
«4» ставится за 5 верно решенных задания;
«3» ставится за 3-4 верно решенных задания;
«2» - если решено менее 3 заданий.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
Тема 2.2 Координаты и векторы.
Практическая работа № 12
Тема: Действия над векторами.
Цель: закрепление знаний, отработка навыков выполнения действий над векторами.
Пояснения к работе:
Основные формулы:
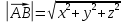
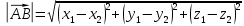 ;
; 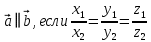 ;
; 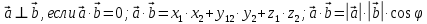 ;
; 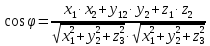 ;
; 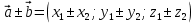 ; m
; m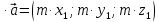 ;
;Пример: 1) Дано:
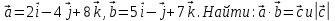
Решение:
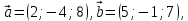
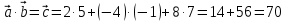 .
.2) Коллинеарны ли векторы
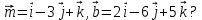 Ответ: Нет, т. к.
Ответ: Нет, т. к. 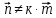
3) Найти угол между векторами
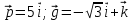 . Решение:
. Решение: 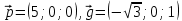 ,
, 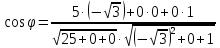 =
= 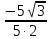 = -
= - 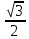
Задания к практической работе:
| Вариант 1 | Вариант 2 |
| 1. Дано: 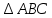 , А , А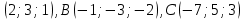 Найти: а) координаты 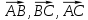 б) длину вектора 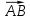 в) сумму и разность векторов 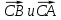 г) 3 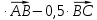 д) периметр 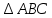 | 1. Дано: 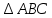 , А , А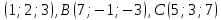 Найти: а) координаты 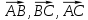 б) длину вектора 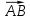 в) сумму и разность векторов 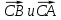 г) 5 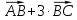 д) периметр 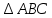 |
| 2. Определить коллинеарность 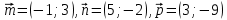 | векторов: 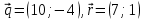 |
| 3.  На оси ОХ найти точку, равноудаленную от точек А На оси ОХ найти точку, равноудаленную от точек А 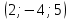 и В и В 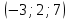 | 3. На оси ОZ найти точку, равноудаленную от точек 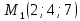 и и 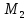 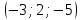 |
| 4. Найти угол 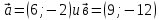 | между векторами: 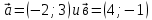 |
| 5. Найти точку, делящую отрезок между точками А (-2;3) и В (4;6) в отношении 2 : 3 | 5. Серединой отрезка является точка (-1;2) и одним из его концов точка (2;5). Найти координаты второго конца отрезка. |
Критерии оценки:
«5» ставится за 5 верно решенных заданий;
«4» ставится за 4 верно решенных задания;
«3» ставится за 3 верно решенных задания;
«2» - если решено менее 3 заданий.
Литература.
Атанасян Л.С., Бутузов В.Ф. Геометрия, 10–11: учебник для общеобразовательных учреждений: базовый и профильный уровни. 21-е изд. М.: Просвещение, 2012. 255с.: ил.
Раздел 3 ОСНОВЫ ТРИГОНОМЕТРИИ
Тема 3.1. Основные тригонометрические тождества
Практическая работа № 13
Использование формул приведения для преобразования тригонометрических выражений.
Цель работы: закрепление знаний, отработка навыков работы с формулами приведения.
Таблица формул приведения.
| Функция | Аргументы | |||
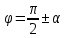 | 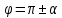 | 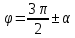 | 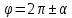 | |
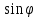 | cosa | +sina | -cosa | - sina |
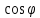 | +sina | -cosa | +sina | cosa |
| tg 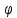 | +ctga | +tga | +ctga | -tga |
| ctg 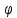 | +tga | +ctga | +tga | -ctga |
Пример 1. Найдите значение
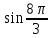
Решение.
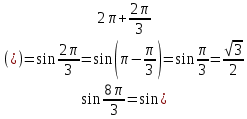
Пример 2.
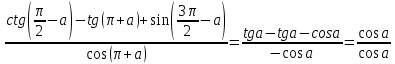 =1
=1Задания к практической работе.
| Вариант 1 | Вариант 2 |
| 1. Перевод градусной меры в радианную и радианной в градусную а) 30 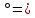 б) 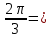 в) 2 рад. = г) Найдите градусную и радианную величину центрального угла шага зубчатого колеса, имеющего 72 зуба. | Перевод градусной меры в радианную и радианной в градусную а) 12 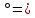 б) 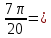 в) 3 рад.= г) Окружность морских компасов делится на 32 равные дуги, называемые румбами. Вычислите градусную и радианную меры румба. |
| 2. Установите знаки значений а) 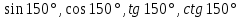 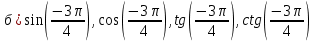 в) 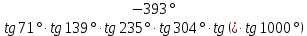 | тригонометрических функций: 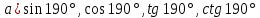 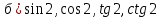 в) 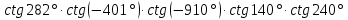 |
| 3. Вычислите: 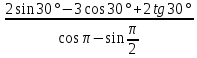 | 3. Вычислите 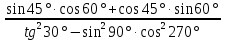 |
| 4) Упростите 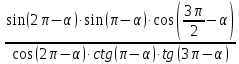 | выражение: 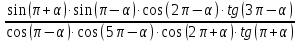 |