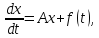Файл: 17.06.вкр.docx

Федеральное государственное бюджетное

ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ЕЛЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМ. И. А. БУНИНА»

Физико-математический факультет

Кафедра математического анализа и элементарной математики

ЧИСЛЕННЫЕ МЕТОДЫ ПРИБЛИЖЁННОГО РЕШЕНИЯ ЗАДАЧИ КОШИ ДЛЯ ОДНОРОДНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В БАНАХОВОМ ПРОСТРАНСТВЕ

Выпускная квалификационная работа студентки гр. ПМ-51

Дедовой Татьяны Алексеевны.

Научный руководитель

канд. ф.-м. наук

доцент Елецких И.А

ВКР допущена к защите

« ___»___________2014г. (протокол №____)

Зав. кафедрой ________ О.А. Саввина

Елец-2014

Содержание

Введение…………………………………………………………………..……..3

ГЛАВА 1. Линейные дифференциальные уравнения первого и второго порядка с постоянным оператором в банаховом пространстве…………9

§1. Решение однородного и неоднородного уравнений в векторной и операторной формах……………………………………………………………

§2. Исследование поведения решений однородного уравнения на бесконечности…………………………………………………………………..

§3. Ограниченность решений однородного уравнения……………………….

§4. Условия существования ограниченного решения у неоднородного уравнения………………………………………………………………………..

ГЛАВА 2. Численные методы приближённого решения задачи Коши для линейного дифференциального уравнения.

§5.Общие сведения о дифференциальных уравнениях………………………

§6.Численные методы решения задачи Коши для обыкновенного дифференциального уравнения первого порядка……………………………….

§7. Метод Эйлера………………………………………………………………..

§8. Метод Эйлера-Коши…………………………………………………………

§9. Метод Рунге-Кутта……………………………………………………………

§10. Решение краевых задач для линейных дифференциальных уравнений второго порядка методом конечных разностей………………...........................

§11.Метод сеток для решения дифференциальных уравнений в частных производных……………………………………………………………………

Введение

1. Задачи, относящиеся к теории дифференциальных уравнений, появились на рубеже XVI – XVII веков в связи с решением различных проблем физики, математики, механики. Перед создателями анализа задача интегрирования дифференциальных уравнений вначале рассматривалась как часть общей задачи: обратной задачи анализа бесконечно малых. Естественно внимание вначале сосредоточилось на различных уравнениях первого порядка, при решении которых использовалось разделение переменных.

В 1692 году И. Бернулли нашел другой прием, использовав в ряде задач умножение на интегрирующий множитель. Арсенал приемов решения дифференциальных уравнений включал также замену переменных, которую впервые в 1693 году применил Лейбниц при решении однородных уравнений первого порядка. С 1693 года И. Бернулли работал над методами последовательного понижения порядка уравнения.

Однако эти, а также некоторые другие приемы были разрознены, а количество задач, сводимых к дифференциальным уравнениям, гигантски росло. Все прикладные задачи, известные в то время, требовали решения многочисленных и разнообразных дифференциальных уравнений. В начале XVIII века эти задачи не могли быть решены, т. к. был слаб аппарат, пригодный для решения дифференциальных уравнений.

Новые результаты стали появляться в 20-х годах XVIII века. В 1724 году итальянский математик Я. Риккати опубликовал исследование нелинейного дифференциального уравнения

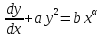
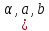- постоянные), названного по предположению Даламбера (1769) уравнением Риккати. К концу 30-х годов XVIII века Эйлер разработал алгоритм решения линейных дифференциальных уравнений с постоянными коэффициентами, основанный на понижении порядка некоторых однородных уравнений с помощью показательной функции. Даламбер в 1766 году нашел, что общее решение неоднородного линейного уравнения равно сумме некоторого частного решения и общего решения соответствующего однородного уравнения. Практические успехи, достигнутые крупнейшими учеными XVIII века в решении дифференциальных уравнений, оказались в 60-х годах настолько значительными, что создалась объективная возможность для построения общей теории дифференциальных уравнений. Первое систематическое изложение теории дифференциальных уравнений было выполнено Эйлером в его трехтомном сочинении «Интегральное исчисление», вышедшее в свет в 1768-1770 годах.

Однако ученые этого времени основную проблему видели в разработке и поиске методов решения новых типов уравнений, существование которых полагалось очевидным. Перестройка математического анализа в XIX веке затронула не только уточнение определений основных понятий науки (предел, производная, интеграл и др.), но и поставила на первый план проблемы доказательства существования и единственности определяемых объектов анализа. Это коснулось и теории дифференциальных уравнений (задача Коши о существовании и единственности решения обыкновенных дифференциальных уравнений).

К 70-м годам XIX века проблема интегрирования обыкновенных дифференциальных уравнений в квадратурах элементарных функций утратила свою прежнюю актуальность. Было установлено, что круг уравнений, имеющих такие решения, чрезвычайно узок и в теории дифференциальных уравнений особое значение приобрели методы численного интегрирования. Но вскоре обнаружились недостатки и этих методов: во-первых, они были весьма трудоемки, а, во-вторых, не раскрывали общей картины поведения интегральных кривых, как того требовали задачи теоретической механики и техники. Поэтому следующим этапом в истории дифференциальных уравнений стало создание качественной теории устойчивости (А. Пуанкаре (1854 – 1912), А. М. Ляпунов (1857 – 1918)).

В начале XX века возникло новое направление в анализе, развивавшееся позднее в предмет, известный теперь под названием функциональный анализ. Его развитие вызвано, прежде всего, потребностями дифференциальных уравнений, численных методов, математического программирования и других разделов математики. Первое абстрактное изложение предмета содержится в диссертации С. Банаха 1920 года. До середины 40-х годов интересы специалистов по функциональному анализу были сфокусированы почти исключительно на изучении нормированных пространств. Развитие квантовой механики дало толчок к изучению теории операторов, что привело к систематическому изучению операторных алгебр (фон Нейман, М. Нагумо, И. М. Гельфанд). В 1950 году Л. Шварцем построена теория распределений, которая легла в основу общей теории локально выпуклых пространств. Работам Шварца предшествовали работы С. Бохнера, И. М, Гельфанда, С. Л. Соболева. Но именно Шварц превратил все в очень мощный и плавно действующий аппарат, который оказался пригодным для многих приложений, особенно к дифференциальным уравнениям.

Следует отметить, что методы функционального анализа успешно применяются для исследования поведения решения дифференциального уравнения, т. к. позволяют провести рассуждения в общем случае, опираясь лишь на свойства операторов.

Целью выпускной квалификационной работы является изучение средствами функционального анализа линейного дифференциального уравнения с постоянным оператором в банаховом пространстве, решение задачи Коши.

Объект исследования: дифференциальное уравнение 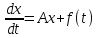, где– постоянный оператор,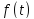– непрерывная вектор–функция.

Предмет исследования: процесс разработки и реализации вычислительного алгоритма для решения задачи Коши численными методами.

Для достижения цели в соответствии с объектом и предметом исследования поставлены следующие задачи:

1. изучить историю возникновения и развития теории дифференциальных уравнений;

2. изучить решение однородного и неоднородного уравнений через операторную экспоненту;

3. рассмотреть условия ограниченности однородного уравнения;

4. изучить поведение решений на бесконечности в связи с характером расположения спектра оператора ;

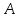5. рассмотреть практические методы решения задачи Коши;

6. разработать вычислительный алгоритм, реализаций решений дифференциальных уравнений.

2. В выпускной квалификационной работе изучается линейное уравнение

где 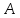– постоянный оператор,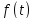– непрерывная вектор–функция. рассматриваются приближенные методы решения задачи Коши для линейного дифференциального уравнения. Работа состоит из введения, двух глав, 11 параграфов и списка литературы,содержащего 15 наименований (всего 59 страниц машинописного текста).

Глава 1 посвящена изучению общих вопросов теории уравнений (1) с точки зрения известных свойств операторов.

В §1 выводятся формулы, позволяющие выразить решение однородного и неоднородного уравнений через операторную экспоненту 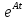. Рассматриваются некоторые линейные уравнения в пространстве операторов.

В §2 изучается поведение решений однородного уравнения на бесконечности в связи с характером расположения спектра 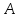, выясняется геометрический смысл рассматриваемых фактов.

В §3 исследуются условия ограниченности на всей действительной оси решений однородного уравнения. Здесь рассматривается и уравнение второго порядка с оператором, действующим в прямой сумме двух банаховых пространств.

§4 посвящен изучению неоднородного уравнения. Здесь вводится важное понятие функции Грина и с помощью этой функции рассматривается ряд задач, касающихся условий существования ограниченных на всей оси и на полуоси решений.

Глава 2 посвящена изучению численных методов,с помощью которых осуществляется решение задачи Коши для уравнения (1).

§5 посвящен общим сведениям о дифференциальных уравнениях, рассматриваются некоторые определения и теоремы.

В §6 рассматривается постановка задачи Коши для системы обыкновенных дифференциальных уравнений (1), изучается формула погрешности для характеристики точности численного метода, рассмотрены некоторые определения.

В §7 исследуется метод Эйлера, выясняется геометрическая интерпретация данного метода, приведены примеры решения и реализация метода в математическом пакете.

§8посвящен изучению метода Эйлера-Коши, здесь рассматривается отличительная особенность метода Эйлера-Коши от метода Эйлера, выясняется геометрическая интерпретация данного метода, приведены примеры решения и реализация данного метода решения в математическом пакете.

В §9 исследуется метод Рунге-Кутта, выводятся соответствующие формулы, рассматривается такое понятие, как основной прием Рунге-Кутта, приведены примеры и реализация данного метода в системе компьютерной математики Maxima.

§10 рассматривает решение краевых задач для уравнений второго порядка методом конечных разностей, приведены соответствующие примеры.