ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 189
Скачиваний: 0
СОДЕРЖАНИЕ
Федеральное государственное бюджетное
§2. Исследование поведения решений однородного уравнения на бесконечности
§3. Ограниченность решений однородного уравнения
§4.Условия существования ограниченного решения у неоднородного уравнения
§5. Общие сведения о дифференциальных уравнениях
Реализация метода Рунге-Кутта с помощью системы Maxima
Реализация конечно-разностного метода
§ 11. Метод сеток для решения дифференциальных уравнений в частных производных
Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima
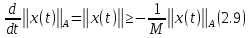
Проинтегрировав это неравенство, мы видим, что
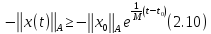
т.
е решения с начальными значениями из
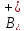 неограниченно возрастают при
неограниченно возрастают при .
.
Заметим,
что из разложения
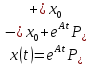 следует, что любое решение, для которого
следует, что любое решение, для которого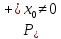 ,
неограниченно возрастает. В частности,
если весь спектр лежит внутри правой
полуплоскости, то
,
неограниченно возрастает. В частности,
если весь спектр лежит внутри правой
полуплоскости, то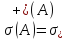 и ненулевое решение
и ненулевое решение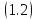 уходит на бесконечность при
уходит на бесконечность при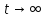 ,
причем норма
,
причем норма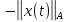 монотонно возрастает.
монотонно возрастает.
Определение
2.1 Оператор
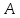 со спектром, распадающимся на два
спектральным множества соответственно
внутри правой и левой полуплоскости
со спектром, распадающимся на два
спектральным множества соответственно
внутри правой и левой полуплоскости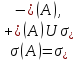 каждое из которых непусто, называетсяэ-дихотомическим.
Вместе с ним будем называть э -
дихотомическим и дифференциальное
уравнение
каждое из которых непусто, называетсяэ-дихотомическим.
Вместе с ним будем называть э -
дихотомическим и дифференциальное
уравнение
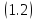 .
.
Очевидно,
что фазовое пространство
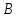 э-дихотомического
уравнения
распадается в прямую сумму
э-дихотомического
уравнения
распадается в прямую сумму
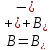 ,
причем решения, начинающиеся в
,
причем решения, начинающиеся в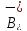 ,
экспоненциально убывают, а решения,
начинающиеся в
,
экспоненциально убывают, а решения,
начинающиеся в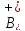 ,
экспоненциально растут.
,
экспоненциально растут.
Если
предположить, фазовое пространство
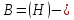 гильбертово,
то все рассуждения естественно проводить,
рассматривая вместо норм
гильбертово,
то все рассуждения естественно проводить,
рассматривая вместо норм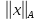 гильбертовы нормы
гильбертовы нормы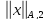 [12].
В этом случае проведенная выше
перенормировка имеет простой геометрический
смысл.
[12].
В этом случае проведенная выше
перенормировка имеет простой геометрический
смысл.
Пусть
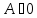 .
Тогда для решения уравнения
.
Тогда для решения уравнения
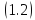 справедливо
соотношение
справедливо
соотношение
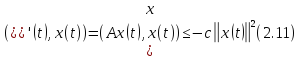
из
которого следует, что для угла
 между направлением радиус-вектора
между направлением радиус-вектора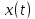 и вектора
и вектора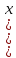 ,
касательного к интегральной кривой
уравнения
,
касательного к интегральной кривой
уравнения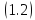 ,
имеет
место оценка
,
имеет
место оценка
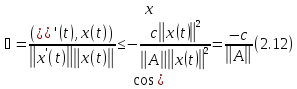
Таким
образом,
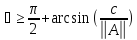 и векторное поле касательных к интегральным
кривым уравнения
и векторное поле касательных к интегральным
кривым уравнения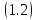 в каждой точке направлено существенно
внутрь сферы с центром в нуле, проходящей
через эту точку.
в каждой точке направлено существенно
внутрь сферы с центром в нуле, проходящей
через эту точку.
Рассмотрим
теперь более общую ситуацию, когда
спектр
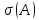 лежит внутри левой полуплоскости. В
этом случае по теоремеI.
5.1.1[1] существует
ограниченный равномерно положительный
оператор
лежит внутри левой полуплоскости. В
этом случае по теоремеI.
5.1.1[1] существует
ограниченный равномерно положительный
оператор
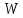 ,
такой, что
,
такой, что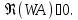
Приведенные
ранее соображения останутся справедливыми,
если оценки производить в новой метрике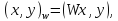 эквивалентной прежней.
эквивалентной прежней.
В
самом деле, ограниченность и равномерная
положительность оператора
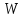 обеспечивают топологическую эквивалентность
норм.
обеспечивают топологическую эквивалентность
норм.
С
другой стороны, если
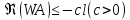 ,
то для решения
,
то для решения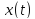 уравнения
уравнения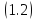 будем иметь
будем иметь
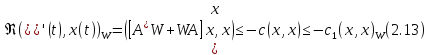
Напомним,
что требуемый оператор
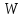 можно
получить как решение уравнения
можно
получить как решение уравнения
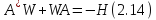
где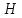 - произвольный, равномерно - положительный
оператор. Полагая, например,
- произвольный, равномерно - положительный
оператор. Полагая, например,
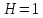 ,[5]
мы получим
,[5]
мы получим
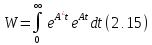
т.е.
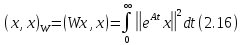
Система
сфер в этом случае заменяется системой
эллипсоидов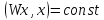 с
центром в нуле, внутрь которых входят
интегральные кривые. Рассмотрение в
банаховом пространстве нормы
с
центром в нуле, внутрь которых входят
интегральные кривые. Рассмотрение в
банаховом пространстве нормы
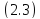 ,
аналогичной
,
аналогичной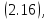 обобщает приведенные выше геометрические
соображения, связанные с так называемым
методом Ляпунова[12].
обобщает приведенные выше геометрические
соображения, связанные с так называемым
методом Ляпунова[12].
Роль
эллипсоидов при этом играют выпуклые
центрально-симметрические тела,
ограниченные поверхностями
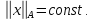
Несколько
более сложная, но достаточно ясная
геометрическая картина получается и в
том случае, когда спектр оператора
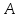 имеет также компоненту, внутри правой
полуплоскости, т.е. когда уравнение
имеет также компоненту, внутри правой
полуплоскости, т.е. когда уравнение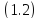 является э-дихотомическим.
является э-дихотомическим.
Рассмотрим
случай, когда фазовое пространство
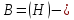 гильбертово.
Справедлива теорема [12]
гильбертово.
Справедлива теорема [12]
Теорема
2.1 Для
того, чтобы уравнение
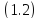 было э - дихотомическим,
необходимо и достаточно, чтобы оператор
было э - дихотомическим,
необходимо и достаточно, чтобы оператор
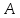 был равномерно
был равномерно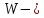 диссипативным
по отношению к некоторому эрмитову
индефинитному оператору
диссипативным
по отношению к некоторому эрмитову
индефинитному оператору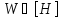 :
:
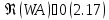
При
любом выборе оператора удовлетворяющего
этому соотношению, инвариантное
подпространство
удовлетворяющего
этому соотношению, инвариантное
подпространство
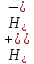 оператора
оператора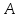 ,
соответствующее части спектра
,
соответствующее части спектра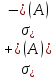 ,
лежащей внутри правой (левой) полуплоскости,
равномерно
,
лежащей внутри правой (левой) полуплоскости,
равномерно
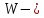 отрицательно
(
отрицательно
(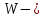 положительно).
положительно).
Индефинитная
форма
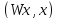 порождает в гильбертовом пространстве
порождает в гильбертовом пространстве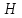 две системы гиперболоидов: плюс
гиперболоиды
определяются уравнением
две системы гиперболоидов: плюс
гиперболоиды
определяются уравнением
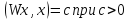 и минус-гиперболоиды
– при
и минус-гиперболоиды
– при
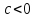 .
.
Нетрудно
проверить, что из равномерной
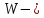 диссипативности
оператора
диссипативности
оператора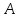 следует для решений уравнения
следует для решений уравнения
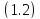 соотношение
соотношение
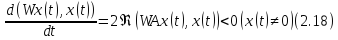
показывающее,
что индефинитная форма
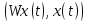 убывает для любого решения
убывает для любого решения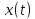 этого уравнения.
этого уравнения.
Если
точка
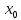 находится
на минус
находится
на минус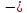 гиперболоиде, то дальнейшее уменьшение
величины
гиперболоиде, то дальнейшее уменьшение
величины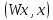 с ростом
с ростом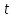 означает,
что траектория
означает,
что траектория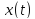 пересекает гиперболоиды со все большими
по абсолютной величине отрицательными
значениями
пересекает гиперболоиды со все большими
по абсолютной величине отрицательными
значениями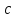 ,
а следовательно, уходит на бесконечность.
,
а следовательно, уходит на бесконечность.
В
случае, когда точка
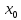 находится
на плюс – гиперболоиде, в подпространстве
находится
на плюс – гиперболоиде, в подпространстве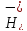 уменьшение формы
уменьшение формы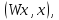 которая на
которая на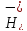 эквивалентна обычной, приводит к
неограниченному приближению траектории
к центру.
эквивалентна обычной, приводит к
неограниченному приближению траектории
к центру.
Если
же точка
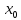 находится
на плюс – гиперболоиде, вне подпространства
находится
на плюс – гиперболоиде, вне подпространства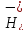 ,
то пересекая гиперболоиды
,
то пересекая гиперболоиды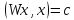 с
уменьшающимися значениями
с
уменьшающимися значениями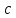 ,
траектория выходит на конус
,
траектория выходит на конус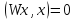 и переходит на систему минус
и переходит на систему минус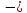 гиперболоидов, удаляясь затем на
бесконечность.
гиперболоидов, удаляясь затем на
бесконечность.
Это
следует из того, что любое решение, для
которого
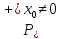 неограниченно возрастает по норме.
неограниченно возрастает по норме.
Заметим
теперь, что подбирая для э
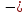 дихотомического оператора
дихотомического оператора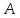 эрмитов оператор
эрмитов оператор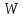 из соотношения
из соотношения
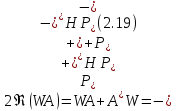
где
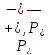 спектральные
проекторы оператора
спектральные
проекторы оператора соответствующие инвариантным
подпространствам
соответствующие инвариантным
подпространствам
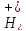 мы придем к форме
мы придем к форме
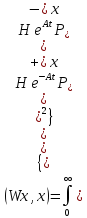
Эта
форма аналогична (при
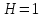 )
индефинитной норме
)
индефинитной норме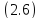 в банаховом пространстве
в банаховом пространстве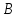 .
.