Файл: 17.06.вкр.docx

,

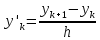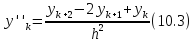
Для концевых точек 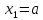и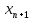=bполагаем

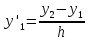и

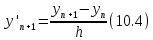
Используя формулы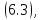дифференциальное уравнение (10.1) при

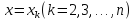приближенно можно заменить системой линейных уравнений

,

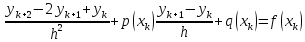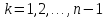
Из формул краевые условиядополнительно дают еще два уравнения

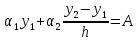
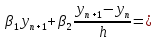B

Таким образом, получаем систему 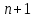линейных уравнений с

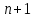неизвестными 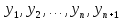, представляющими собой значения искомой функции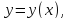

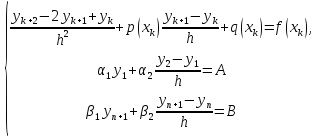
Обозначим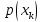=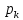,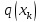=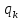,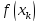=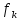. Выполнив алгебраические преобразования над уравнениями, можно привести систему к следующему виду:

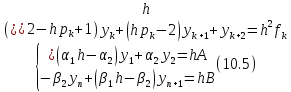
Решив систему, получим таблицу значений искомой функции.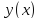

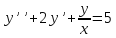Пример Найти решение уравненияна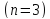с начальными условиями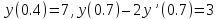

Решение.

Из условия задачи и 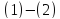следует:

, ,,,,,,.

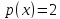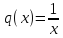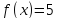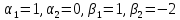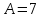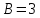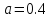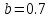Разобьем отрезок [a,b] на равные части с шагом

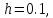
Точки разбиения имеют абсциссы

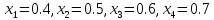
Построим систему 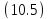линейных алгебраических уравнений, где неизвестными являются.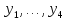

Для коэффициентов основной матрицы системы для n-1 уравнений введем обозначения: ,,

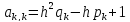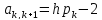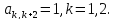
Для коэффициентов последних двух уравнений введем обозначения,,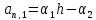

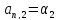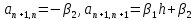
Для матрицы свободных членов введем обозначения:

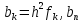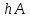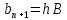= ,,k=1, 2, n =3, h=0.1

Остальные коэффициенты системы равны нулю.

Составим развернутую систему (10.5) для нашей задачи:

(

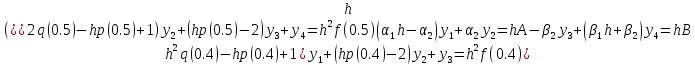
Представим систему в матричном виде:

=

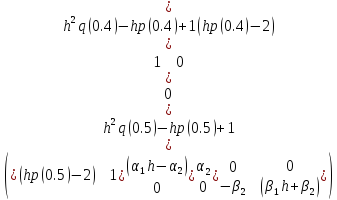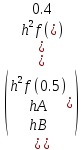
Подставим значения переменных в систему:

=

=

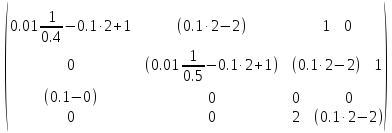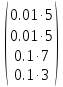
После упрощения получим:

=

Решая полученную систему, найдем приближенное решение дифференциального уравнения:.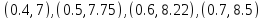

Реализация конечно-разностного метода

Выполним решение краевой задачи конечно-разностным методом в системе Maxima.

Вводим обозначения и задаем значения переменных:

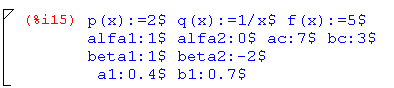
Разбиваем отрезок [a ,b] на равные части с шагом .

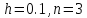Формируем список, содержащий все точки отрезка:

Сформируем пустую квадратную матрицу размера:

Теперь заполним матрицу, для заполнения коэффициентами первых двух уравнений системы воспользуемся циклом с параметром:

В двух последних уравнениях поменяем значения некоторых элементов с помощью оператора присваивания:

Теперь заполним столбец свободных членов:

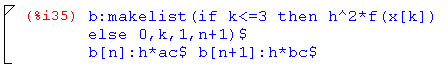
Выведем полученные матрицы на экран:

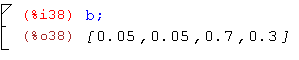
Получили систему линейных уравнений, записанную в матричном ви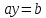де , где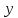— искомое решение. Найдем его матричным способом.

§ 11. Метод сеток для решения дифференциальных уравнений в частных производных

Для решения дифференциального уравнения методом конечных разностей (сеток) сначала область, на которой ищется решения, заменяется дискретным множеством точек (разностной сеток). В этой методе, правило, используется регулярные сетки, шаг которых либо постоянен, либо меняется по несложному закону.

Пусть в качестве области изменения функции задан прямоугольник. Ос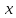ии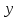разбиваются на отрезки, которые являются шагами сетки по соответствующим направлениям. Через точки деления проводятся прямые, параллельные осям координат. Совокупность точек пересечения (узлов) этих прямых и образует сетку в заданной двумерной области.

Определение 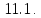Узлы, расстояние между которыми равно шагу сетки по одной из осей, называются соседними.

Способ построения сетки не меняется и в том случае если задана область произвольной формы.

Определение 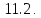Узлы сетки, попавшие внутрь области, называются внутренними узлами.

Определение 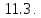Точки пересечения прямых, образующих сетку с границей области называются граничными узлами.

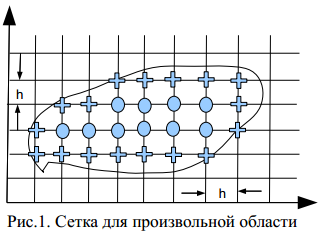
Для двумерной области произвольной формы сетка в общем случае всегда является нерегулярной, причем особенности геометрии учитываются только в околограничных точках

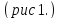
Прежде чем приступать к решению дифференциального уравнения, оно само и граничные условия заменяются разностными аналогами. Вспомним ряд Тейлора для функции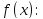

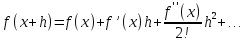
Если оборвать этот ряд на втором члене, то получим

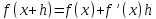или .

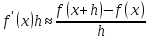Определение 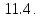Выражение, стоящее в правой части, называется правой разностной производной.