ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 183
Скачиваний: 0
СОДЕРЖАНИЕ
Федеральное государственное бюджетное
§2. Исследование поведения решений однородного уравнения на бесконечности
§3. Ограниченность решений однородного уравнения
§4.Условия существования ограниченного решения у неоднородного уравнения
§5. Общие сведения о дифференциальных уравнениях
Реализация метода Рунге-Кутта с помощью системы Maxima
Реализация конечно-разностного метода
§ 11. Метод сеток для решения дифференциальных уравнений в частных производных
Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima
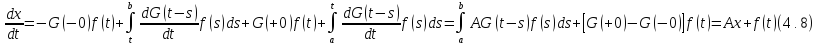
В
дальнейшем, как правило, будем рассматривать
случай, когда спектр
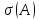 не
пересекается с мнимой осью (в частности,
когда оператор
не
пересекается с мнимой осью (в частности,
когда оператор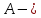 дихотомичен):
дихотомичен):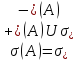 .
.
Определение 4.2 Функцию Грина, определяемую формулой
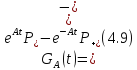
назовем
главной
функцией Грина
уравнения
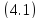 .
.
В
формуле
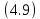 принимается
принимается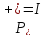 ,
,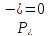 при
при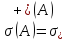 и
и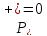 ,
,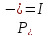 при
при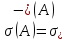 .
.
Поскольку
спектр
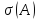 не пересекается с мнимой осью, существуют
числа
не пересекается с мнимой осью, существуют
числа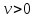 и
и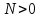 ,
при которых справедлива оценка [8]
,
при которых справедлива оценка [8]
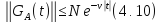
Главная
функция Грина
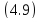 играет важную роль при выяснении условий
существования ограниченного на всей
оси решения уравнения
играет важную роль при выяснении условий
существования ограниченного на всей
оси решения уравнения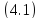 .
В
частности справедлива теорема [8]
.
В
частности справедлива теорема [8]
Теорема
4.1. Для
того чтобы любой ограниченный на всей
оси непрерывной вектор – функции
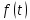 соответствовало
одно и только одно ограниченное на всей
оси решение уравнения
соответствовало
одно и только одно ограниченное на всей
оси решение уравнения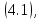 необходимо
и достаточно, чтобы спектр
необходимо
и достаточно, чтобы спектр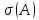 не пересекался с мнимой осью. Это решение
дается формулой
не пересекался с мнимой осью. Это решение
дается формулой
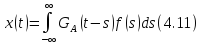
где
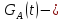 главная функция Грина уравнения
главная функция Грина уравнения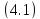 .
.
Доказательство.
Пусть
любому ограниченному непрерывному
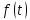 соответствует
ограниченное решение. Положим
соответствует
ограниченное решение. Положим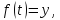 где
где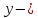 постоянный
вектор, и пусть
постоянный
вектор, и пусть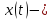 единственное ограниченное решение
уравнения
единственное ограниченное решение
уравнения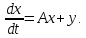
Вектор
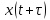 при любом
при любом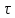 также является решением этого уравнения,
и в силу единственности
также является решением этого уравнения,
и в силу единственности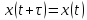 ,
т.е.
,
т.е.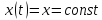 ,
откуда
,
откуда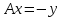 .
.
Из
произвольности
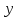 следует, что линейный непрерывный
оператор
следует, что линейный непрерывный
оператор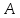 отображает пространство
отображает пространство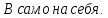 По теореме Банаха (I.1.1)[1]такой
оператор обладает непрерывным обратным
оператором
По теореме Банаха (I.1.1)[1]такой
оператор обладает непрерывным обратным
оператором
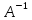 ,
т.е. точка
,
т.е. точка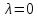 является регулярной точкой оператора
является регулярной точкой оператора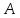 .
.
Пусть
теперь
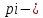 произвольное
чисто мнимое число. Рассмотрим уравнение
произвольное
чисто мнимое число. Рассмотрим уравнение
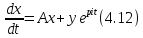
Подстановка
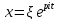 дает
дает
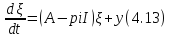
Повторяя
проведенные выше рассуждения, получим,
что оператор
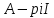 имеет непрерывный обратный оператор,
т.е.
имеет непрерывный обратный оператор,
т.е.
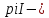 регулярная точка.
регулярная точка.
Тем
самым необходимость условия теоремы
доказана. Для доказательства достаточности
воспользуемся оценкой
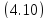 .
Из этой оценки следует, что вектор –
функция
.
Из этой оценки следует, что вектор –
функция
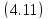 ограничена:
ограничена:
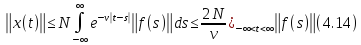
Тот
факт, что эта функция удовлетворяет
уравнению
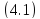 при
при
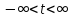 был
установлен ранее [1].
был
установлен ранее [1].
Остается
показать единственность ограниченного
решения. Для этого достаточно проверить,
что однородное уравнение
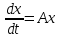 не имеет ограниченных на всей оси
решений, отличных от тривиального.
не имеет ограниченных на всей оси
решений, отличных от тривиального.
Допустим,
что такое решение
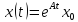 существует. Полагая
существует. Полагая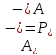 ,
, ,
его можно записать в виде
,
его можно записать в виде
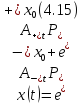
Поскольку
спектром оператора
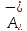 в пространстве
в пространстве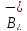 является
множество
является
множество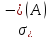 ,
лежащее внутри левой полуплоскости, то
первое слагаемое ограничено при
,
лежащее внутри левой полуплоскости, то
первое слагаемое ограничено при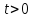 ,
а значит, этим свойством обладает и
второе слагаемое
,
а значит, этим свойством обладает и
второе слагаемое
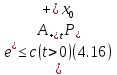
Но
тогда, учитывая тот факт, что спектр
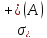 оператора
оператора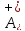 в пространстве
в пространстве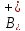 (если он не пуст) лежит внутри правой
полуплоскости, мы получим
(если он не пуст) лежит внутри правой
полуплоскости, мы получим
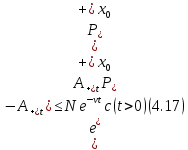
Это
неравенство при
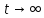 показывает, что
показывает, что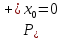 .
Аналогично показывается, что и при
.
Аналогично показывается, что и при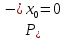 .
Теорема доказана.
.
Теорема доказана.
Глава 2. Численные методы приближенного решения задачи Коши для однородных дифференциальных уравнений в банаховом пространстве
§5. Общие сведения о дифференциальных уравнениях
При изучении физических явлений часто не удается непосредственно найти закон, связывающий независимые переменные и искомую функцию, но можно установить связь между этой функцией и ее производными, выражаемую дифференциальным уравнением. Приведём основные понятия теории дифференциальных уравнений [15].
Определение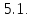 Уравнение,
связывающее независимую переменную
Уравнение,
связывающее независимую переменную
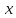 ,
искомую функцию
,
искомую функцию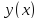 и её производные
и её производные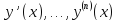 ,
т.е уравнение вида
,
т.е уравнение вида
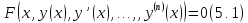
называется дифференциальным уравнением.
Здесь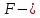 известная функция,
известная функция,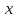 -
независимое переменное,
-
независимое переменное,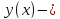 неизвестная функция.
неизвестная функция.
Определение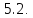 Если
искомая функция
Если
искомая функция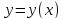 есть функция одной переменной, то
дифференциальное уравнение называетсяобыкновенным.
есть функция одной переменной, то
дифференциальное уравнение называетсяобыкновенным.
Определение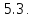 Порядком
дифференциального уравнения называется
наивысший порядок входящих в него
производных.
Порядком
дифференциального уравнения называется
наивысший порядок входящих в него
производных.
Определение
5.4. Решением
дифференциального
уравнения
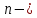 го
порядка на интервале
го
порядка на интервале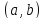 называется функция
называется функция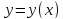 ,
определенная на отрезке
,
определенная на отрезке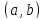 вместе со своими производными до
вместе со своими производными до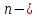 го
порядка включительно, и такая, что
подстановка функции
го
порядка включительно, и такая, что
подстановка функции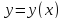 в дифференциальное уравнение превращает
последнее в тождество по
в дифференциальное уравнение превращает
последнее в тождество по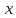 на
на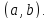
Дифференциальное
уравнение
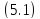 имеет бесконечно многорешений.
имеет бесконечно многорешений.
Определение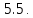 Множество
всех решений уравнения
Множество
всех решений уравнения
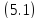 называетсяобщим
решением
уравнения
называетсяобщим
решением
уравнения
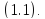 Всякое
отдельно взятое решение называется егочастным
решением.
Всякое
отдельно взятое решение называется егочастным
решением.
Определение
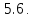 Задача
для нахождения
Задача
для нахождения
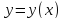 уравнения
уравнения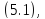 удовлетворяющего начальным условиям
удовлетворяющего начальным условиям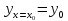 ,
,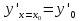 ,…,
,…,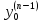 ,
называетсязадачей
Коши
для уравнения
,
называетсязадачей
Коши
для уравнения
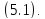
Известна теорема существования и единственности решения задачи Коши[12].
Теорема
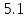 .Если
в уравнении
.Если
в уравнении
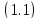 функция
функция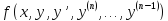
непрерывна по всем своим аргументам
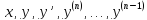 в некоторой области
в некоторой области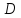 их
изменения;
их
изменения;имеет ограниченные в области
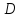 частные производные
частные производные
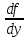 ,
,
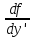 ,
,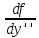 ,…,
,…,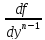 по аргументам
по аргументам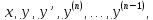
то
найдется интервал
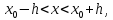 на котором существует единственное
решение
на котором существует единственное
решение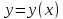 ,
удовлетворяющее условиям
,
удовлетворяющее условиям
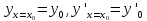 ,…,
,…,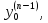 где значения
где значения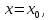 y
=
y
=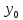 ,
,