ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 16.04.2024
Просмотров: 190
Скачиваний: 0
СОДЕРЖАНИЕ
Федеральное государственное бюджетное
§2. Исследование поведения решений однородного уравнения на бесконечности
§3. Ограниченность решений однородного уравнения
§4.Условия существования ограниченного решения у неоднородного уравнения
§5. Общие сведения о дифференциальных уравнениях
Реализация метода Рунге-Кутта с помощью системы Maxima
Реализация конечно-разностного метода
§ 11. Метод сеток для решения дифференциальных уравнений в частных производных
Выполним реализацию конечно-разностного метода в системе компьютерной математики Maxima
§11посвящен методу сеток для решения дифференциальных уравнений в частных производных, рассматриваются важные определения, приведены примеры.
В работе принята единая нумерация параграфов. Нумерация формул своя в пределах каждого параграфа. Формулы имеют двойную нумерацию: например, (2.1) означает, что речь идет о формуле 1 из §2.
Основные результаты ВКР докладывались на заседаниях кафедры математического анализа и элементарной математики, на заседаниях НСО, на научно-практической конференции преподавателей и студентов физико-математического факультета 9 апреля 2014 года.
ГЛАВА 1. Линейные дифференциальные уравнения первого и второго порядка с постоянным оператором в банаховом пространстве.
§1. Решение однородного и неоднородного уравнений в векторной и операторной формах.
Рассмотрим дифференциальное уравнение
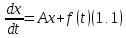
в
банаховом пространстве
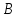 с постоянным оператором
с постоянным оператором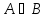 и непрерывной вектор-функцией
и непрерывной вектор-функцией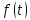 .
.
Определение 1.1 Банаховым пространством называется полное нормированное векторное пространство.
Пространство
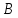 будем называтьфазовым
пространством
уравнения.
будем называтьфазовым
пространством
уравнения.
Обратимся к однородному уравнению
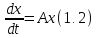
Решение
задачи Коши для уравнения
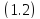 с условием
с условием
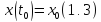
получено
в [12]
с
использованием оператор - функции
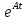 .
.
Вектор-функция
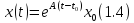
имеет
непрерывную производную и является
решением задачи
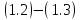 .
Это решение является единственным в
классе дифференцируемых функций.
Достаточно показать, что если непрерывная
функция
.
Это решение является единственным в
классе дифференцируемых функций.
Достаточно показать, что если непрерывная
функция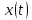 ,
удовлетворяющая уравнению
,
удовлетворяющая уравнению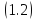 ,
обращается в нуль в точке
,
обращается в нуль в точке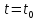 ,
то она обращается в нуль и в некоторой
её окрестности[12].
,
то она обращается в нуль и в некоторой
её окрестности[12].
Такая функция должна удовлетворять уравнению
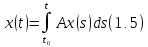
Откуда
следует при
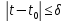 оценка
оценка
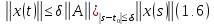
приводящая
при
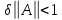 к противоречию, если
к противоречию, если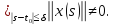
Применяя
метод вариации постоянной, можем найти
решение задачи Коши для неоднородного
уравнения
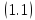 в виде
в виде
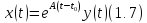
После
такой замены уравнение
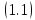 примет вид
примет вид
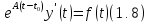
Откуда
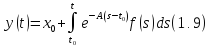
и наконец
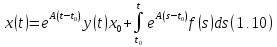
Очевидно,
что выражение
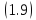 представляет собой дифференцируемую
функцию. Кроме того, решение
представляет собой дифференцируемую
функцию. Кроме того, решение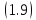 задачи Коши
задачи Коши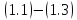 единственно, поскольку единственно
решение задачи Коши для однородного
уравнения.
единственно, поскольку единственно
решение задачи Коши для однородного
уравнения.
Приведём
решение этой задачи в операторной форме.
Предположим, дан оператор
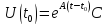 ,
где
,
где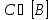 ,
удовлетворяет уравнению
,
удовлетворяет уравнению
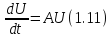
и
условию
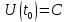 .
.
Рассмотрим более общее операторное уравнение
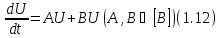
в
фазовом пространстве
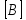 .
Перепишем уравнение
.
Перепишем уравнение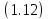 в виде [6]
в виде [6]
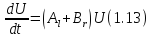
Поскольку
операторы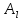 и
и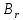 коммутируют,
решение уравнения
коммутируют,
решение уравнения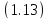 ,
удовлетворяющее
условию
,
удовлетворяющее
условию
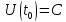 имеет вид
имеет вид
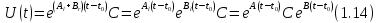
Точно так же можно получить для решения уравнения
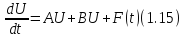
где
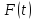 -
непрерывная
функция со значениями из
-
непрерывная
функция со значениями из
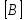 формулу
формулу
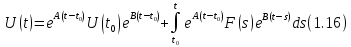
§2. Исследование поведения решений однородного уравнения на бесконечности
Поведение
решений задачи
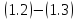 на бесконечности существенно зависит
от расположения спектра оператора
на бесконечности существенно зависит
от расположения спектра оператора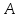 .
.
Предположим,
что спектр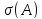 лежит
внутри левой полуплоскости. Тогда из
лежит
внутри левой полуплоскости. Тогда из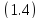 следует на основании теоремыI.1.4
[1] оценка
следует на основании теоремыI.1.4
[1] оценка
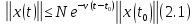
при
любых
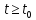 и
некоторых положительных постоянных
и
некоторых положительных постоянных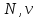 .
.
Верно
и обратное: если оценка
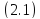 выполняется
для всякого решения
выполняется
для всякого решения
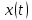 уравнения
уравнения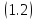 ,
то спектр
,
то спектр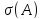 лежит
внутри левой полуплоскости. Действительно,
из
лежит
внутри левой полуплоскости. Действительно,
из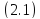 следует,
что
следует,
что
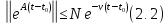
и остается применить теорему I.1.4 [1]:
Поведение
решения уравнения
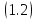 в предположении, что спектр
в предположении, что спектр
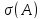 лежит в левой полуплоскости, можно
охарактеризовать более точно, если
ввести новую эквивалентную норму в
пространстве
лежит в левой полуплоскости, можно
охарактеризовать более точно, если
ввести новую эквивалентную норму в
пространстве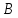 ,
пользуясь формулой
,
пользуясь формулой
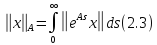
Оказывается,
в этой норме решения уравнения
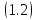 стремятся при
стремятся при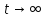 к нулю монотонно. Действительно,
к нулю монотонно. Действительно,
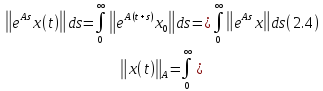
И, таким образом,
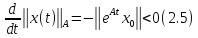
Рассмотрим
теперь случай, когда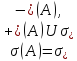 причем спектральное множество
причем спектральное множество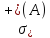 непусто.
непусто.
Пусть
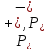 -
спектральные проекторы, соответствующие
этому разложению спектра, и
-
спектральные проекторы, соответствующие
этому разложению спектра, и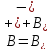 - соответствующее прямое разложение
- соответствующее прямое разложение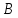 на инвариантные подпространства
оператора
на инвариантные подпространства
оператора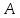 .
Так как
.
Так как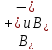 инвариантны относительно операторов
инвариантны относительно операторов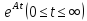 ,
то решение
,
то решение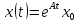 уравнения
уравнения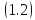 ,
начинающееся в каком - нибудь из них,
уже не выходит из соответствующего
подпространства.
,
начинающееся в каком - нибудь из них,
уже не выходит из соответствующего
подпространства.
Введем
в
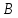 индефинитную норму[8]
индефинитную норму[8]
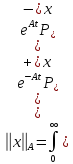
Произведя
вычисления, аналогичные проведенным
выше, получим
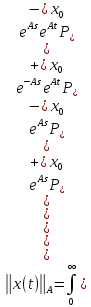
Поэтому
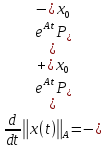
и,
следовательно, индефинитная норма
любого решения уравнения
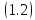 убывает.
убывает.
Рассмотрим два частных случая.
Пусть
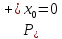 ,
т.е.
,
т.е.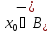 .
В этом подпространстве
.
В этом подпространстве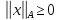 и нормы
и нормы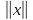 и
и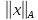 эквивалентны. Из
эквивалентны. Из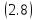 следует, что
следует, что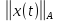 монотонно стремится к нулю.
монотонно стремится к нулю.
Таким
образом, решения
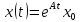 уравнения
уравнения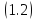 с начальным вектором
с начальным вектором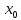 из подпространства
из подпространства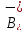 стремятся к нулю.
стремятся к нулю.
Пусть
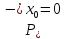 ,
т.е.
,
т.е.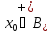 .В
этом подпространстве
.В
этом подпространстве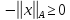 является обычной нормой, эквивалентной
является обычной нормой, эквивалентной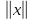 .
Из
.
Из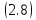 следует, что
следует, что