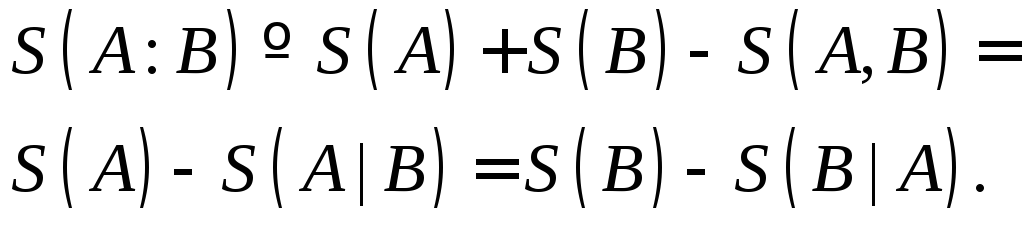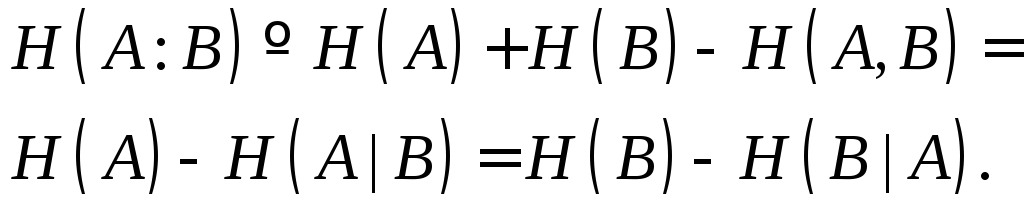ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 08.08.2024
Просмотров: 406
Скачиваний: 0
СОДЕРЖАНИЕ
Теории управления квантовыми системами.
1. Основные понятия и определения квантовой механики
1.1. Чистые и смешанные состояния
2. Элементы квантовой теории информации
2. 3. Преобразование одного кубита
2.5. Перепутывание и квантовая неразличимость
2.6. Логический элемент «управляемое не»
3. Парадокс эйнштейна – подольского – розена (эпр)
5.4 Понятие о квантовой криптографии
5.4.1. Защита посредством неортогональных состояний
5.4.2. Защита посредством перепутывания
5.4.3. Практическая реализация квантово – криптографических систем
6.2. Протокол квантовой телепортации
6. 3. Обзор некоторых экспериментальных результатов по квантовой телепортации
6.4. Заключительные замечания: возможна ли телепортация макрообъекта?
7. Квантовые вычисления. Квантовые компьютеры.
7.4.2. Моделирование вероятности
7.4.3. Алгоритм разложения на простые множители или алгоритм Шора
7.5. Общие требования к квантовым компьютерам Практическая реализация

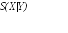
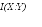
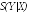
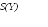


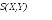
|
Квантовая информация |
Классическая информация |
|
Условная энтропия:
МОЖЕТ БЫТЬ ОТРИЦАТЕЛЬНОЙ |
Условная энтропия:
H(B|A) £ H(B) |
|
Совместная энтропия:
|
Совместная энтропия: H(B) £ H(B|A) |
|
Взаимная информация:
|
Взаимная информация:
|
В теории классической
информации, достижимая информация не
так интересна. Если на практике различение
пары классических состояний может
встретить определенные трудности, то
в принципе, это всегда можно проделать.
В отличие от этого, в квантовом случае,
далеко не всегда возможно различить
два состояния даже в принципе. Например,
не существует однозначной процедуры,
позволяющей различить два неортогональных
состояния. Будем “выражаться” в терминах
достижимой информации. Если Алиса
готовит состояние
![]() с вероятностьюp
и другое неортогональное состояние
с вероятностьюp
и другое неортогональное состояние
![]() с вероятностью1
- p,
то достижимая информация при таком
приготовлении уж точно меньше, чем
H(p),
поскольку Боб не может определить
принадлежность состояния с полной
достоверностью. В классическом случае,
если Алиса готовит два классических
состояния, например, бит - в состоянии
“0” с вероятностью
p
или “1” с
вероятностью 1
- p,
то не существует фундаментального
закона, запрещающего Бобу различить
эти состояния, поэтому достижимая
информация оказывается такой же как и
энтропия приготовления, т.е. H(p).
с вероятностью1
- p,
то достижимая информация при таком
приготовлении уж точно меньше, чем
H(p),
поскольку Боб не может определить
принадлежность состояния с полной
достоверностью. В классическом случае,
если Алиса готовит два классических
состояния, например, бит - в состоянии
“0” с вероятностью
p
или “1” с
вероятностью 1
- p,
то не существует фундаментального
закона, запрещающего Бобу различить
эти состояния, поэтому достижимая
информация оказывается такой же как и
энтропия приготовления, т.е. H(p).
Существует важное замечание, относящееся к этой дискуссии - когда концепция достижимой информации имеет классический смысл. Суть его - в различении распределений вероятностей. Представим, что Алиса готовит состояние “0” или “1” с двумя распределениями вероятностей либо с (p, 1 - p) либо с (q, 1 - q). Получая состояние Боб должен определить, какое распределение вероятности использовала Алиса для приготовления состояния. Очевидно, что Боб не всегда способен определить это с достоверностью 100%. Тем не менее, этот пример (по аналогии с достижимой информацией для квантовой системы, приготавливаемой в одном состоянии из набора смешанных состояний) очень важен. Что является наиболее важным и замечательным - так это то, что фундаментальные объекты в квантовой механике - чистые квантовые состояния - обладают свойствами различимости, что является существенно отличным и существенно богатым свойством, нежели чем для фундаментальных объектов классической теории информации, таких как “0” и “1”.
Теорема о запрете клонирования сулит другую перспективу в плане ограничения на достижимую квантовую информацию по сравнению с классической. Классическая информация, безусловно, может быть копирована. Это точно можно сделать с цифровой информацией, например, создавая копии файлов с текстами, заложенными в компьютер. Теорема о запрете клонирования утверждает, что квантовая механика не позволяет точно копировать неизвестное квантовое состояние и накладывает некоторые ограничения на возможность создания примерных копий.
На первый взгляд,
теорема о запрете клонирования выглядит
довольно странно. В конце концов, не
является ли классическая физика частным
случаем квантовой механики? Почему мы
можем копировать классическую информацию,
если нельзя копировать квантовую? Ответ
состоит в том, что эта теорема не запрещает
копировать все квантовые состояния.
Она лишь утверждает, что нельзя копировать
неортогональные квантовые состояния.
Далее, теорема подразумевает, что
невозможно построить квантовый прибор
так, чтобы при наличии на входе состояний
![]() и
и![]() ,
на выходе будет две копии входного
состояния
,
на выходе будет две копии входного
состояния![]()
![]() или
или![]()
![]() .
С другой стороны, если
.
С другой стороны, если![]() и
и![]() ортогональны, то теорема не запрещает
их копирование. Действительно, довольно
просто сконструировать квантовые схемы,
которые копируют такие состояния. Это
замечание разрешает кажущееся противоречие
между теоремой о запрете клонирования
и способностью копировать классическую
информацию. Для различных состояний
классическая информация может
восприниматься как представляемая
ортогональными состояниями.
ортогональны, то теорема не запрещает
их копирование. Действительно, довольно
просто сконструировать квантовые схемы,
которые копируют такие состояния. Это
замечание разрешает кажущееся противоречие
между теоремой о запрете клонирования
и способностью копировать классическую
информацию. Для различных состояний
классическая информация может
восприниматься как представляемая
ортогональными состояниями.
Теорема о запрете клонирования
Предположим, что
у нас есть квантовое устройство с двумя
портами А
и В.
Порт А
- это порт
данных. В
него помещается неизвестное, но чистое
квантовое состояние
![]() .
Это состояние требуется скопировать
на порте-мишениВ.
Предположим, что порт - мишень изначально
находится в некоем стандартном чистом
состоянии
.
Это состояние требуется скопировать
на порте-мишениВ.
Предположим, что порт - мишень изначально
находится в некоем стандартном чистом
состоянии
![]() .Таким
образом, начальное состояние всего
копирующего устройства есть:
.Таким
образом, начальное состояние всего
копирующего устройства есть:
![]() . (2.19)
. (2.19)
Процедура копирования подвергается некоторой унитарной эволюции U. В идеальном случае такая процедура
![]()
Предположим, что
процедура копирования работает для
каких-нибудь двух особых чистых состояний
![]() и
и![]() .
Тогда,
.
Тогда,
![]() (2.20)
(2.20)
![]() (2.21)
(2.21)
Находя скалярное (= внутреннее) произведение этих двух уравнений, получаем, что
![]()
Унитарность дает
![]() ,
а раскрывая прямое произведение векторов,
и учитывая, что
,
а раскрывая прямое произведение векторов,
и учитывая, что![]() получаем:
получаем:
![]() (2.22)
(2.22)
Но уравнение х2
= х имеет
только два решения: х
= 0 и х
= 1, поэтому
![]() =
=![]() или
или![]() и
и![]() - ортогональны. Следовательно, копирующее
устройство может копировать только
состояния ортогональные друг другу.
Отсюда, в общем случае, квантовые
состояния нельзя копировать (клонировать).
Например, квантовый клон не может
клонировать состояния кубита
- ортогональны. Следовательно, копирующее
устройство может копировать только
состояния ортогональные друг другу.
Отсюда, в общем случае, квантовые
состояния нельзя копировать (клонировать).
Например, квантовый клон не может
клонировать состояния кубита![]() = 0 и
= 0 и![]() ,т.к.
эти состояния неортогональны.
,т.к.
эти состояния неортогональны.
Т.о., квантово-механическая машина, приготавливающая копии квантовых состояний может это сделать лишь для совпадающих или ортогональных состояний. Происходит это из-за того, что, как и все квантовые операции, операция клонирования должна быть унитарной и сохранять скалярное (внутреннее) произведение. Невозможно приготовить совершенную копию неизвестного квантового состояния, используя унитарное преобразование (эволюцию). Если в копирующей машине используются неунитарные операции, то по-прежнему невозможно копировать неортогональные чистые состояния, до тех пор пока не будет удовлетворительного соответствия копируемых состояний исходным. То же относится и к смешанным состояниям.
Рассмотрим проблему копирования несколько с другой стороны. В криптографии при обмене секретными сообщениями необходимо заботиться в возможности перехвата. Тот, кто перехватывает сообщения должен уметь различить неортогональные состояния, поскольку именно их и передает Алиса.
Пусть Ева
приготавливает свой измерительный
прибор в исходном состоянии
![]() .
Ее цель - различить неортогональные
состояния
.
Ее цель - различить неортогональные
состояния![]() и
и![]() не возмущая их. Другими словами, она
хочет выполнить унитарную операцию:
не возмущая их. Другими словами, она
хочет выполнить унитарную операцию:
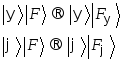
Из унитарности
операции следует, что![]() ,
т.е.
,
т.е.![]() Отсюда видно, что конечное значение
измерительного прибора будет одинаковым
в обоих случаях! Ева не возмутила (не
исказила) два неортогональных состояния,
но она и не получила никакой информации
об этих состояниях, т.к.
Отсюда видно, что конечное значение
измерительного прибора будет одинаковым
в обоих случаях! Ева не возмутила (не
исказила) два неортогональных состояния,
но она и не получила никакой информации
об этих состояниях, т.к.![]() Более
общее измерение, которое возмущает
исходные состояния, так что
Более
общее измерение, которое возмущает
исходные состояния, так что![]() и
и![]() ,
дает
,
дает
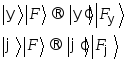
Из унитарности
следует, что
![]() Самый
лучший вариант для Евы, в смысле
оптимального различения двух состояний,
соответствует минимуму выражения
Самый
лучший вариант для Евы, в смысле
оптимального различения двух состояний,
соответствует минимуму выражения![]() .
Минимум осуществляется, когда
.
Минимум осуществляется, когда![]() ,
что как раз означает неразличимость
исходных состояний
,
что как раз означает неразличимость
исходных состояний![]() и
и![]() после операции, выполняемой Евой. Этот
пример служит наглядной иллюстрацией
связи междуинформацией,
извлекаемой при измерении и
возмущением исходных состояний.
после операции, выполняемой Евой. Этот
пример служит наглядной иллюстрацией
связи междуинформацией,
извлекаемой при измерении и
возмущением исходных состояний.
Хорошей мерой того, сколько информации получено Бобом о величине X из его измерений - это взаимная информация между X и результатом измерения Y. Боб может сделать заключение об X по результатам измерения Y только, если и только, если H(X:Y) = H(X), и что в общем случае H(X:Y) H(X). Покажем, что близость величины H(X:Y) к H(X) не самом деле дает хорошую меру того, как Боб смог определить Х. Цель Боба - выбрать измерение, которое максимизирует величину H(X:Y) и тем самым приближая ее к H(X). Для этого, определим достижимую информацию (accessible information), как максимальную величину взаимной информации. Достижимая информация - это мера того, насколько хорошо Боб смог сделать вывод о приготовленном Алисой состоянии, которая она послала ему.
Существует важное замечание, относящееся к этой дискуссии - когда концепция достижимой информации имеет классический смысл. Суть его - в различении распределений вероятностей. Представим, что Алиса готовит состояние “0” или “1” с двумя распределениями вероятностей либо с (p, 1 - p) либо с (q, 1 - q). Получая состояние Боб должен определить, какое распределение вероятности использовала Алиса для приготовления состояния. Очевидно, что Боб не всегда способен определить это с достоверностью 100%. Тем не менее, этот пример (по аналогии с достижимой информацией для квантовой системы, приготавливаемой в одном состоянии из набора смешанных состояний) очень важен. Чистые квантовые состояния обладают свойствами различимости, что является существенно отличным и богатым свойством, чем для фундаментальных объектов классической теории информации, таких как “0” и “1”.
Какова связь между
копированием и достижимой информацией?
Пусть Алиса приготавливает одно из двух
неортогональных состояний
![]() и
и![]() с соответствующими вероятностямиp
и (1 - p).
Предположим, что в этом случае достижимая
информация Боба есть Н(p),
т.е. законами квантовой механики разрешено
Бобу получить достаточно информации
при его измерении о том, какое из двух
состояний
с соответствующими вероятностямиp
и (1 - p).
Предположим, что в этом случае достижимая
информация Боба есть Н(p),
т.е. законами квантовой механики разрешено
Бобу получить достаточно информации
при его измерении о том, какое из двух
состояний
![]() или
или![]() было приготовлено Алисой. Боб может
копировать состояния очень простым
способом. Он бы выполнил измерение,
определив, какое состояние
было приготовлено Алисой. Боб может
копировать состояния очень простым
способом. Он бы выполнил измерение,
определив, какое состояние![]() или
или![]() было приготовлено Алисой и как только
он завершил идентификацию он бы приготовил
копии состояний, которые получил от
Алисы. Таким образом, теорема о запрете
копирования явилась бы следствием того
факта, что достижимая информация об
этих состояниях строго меньше, чемН(p).
Можно обратить эти рассуждения и
показать, что из теоремы о запрете
клонирования следует, что достижимая
информация меньше чем Н(p).
Представим, что возможно клонировать
неортогональные состояния. После
получения состояния
было приготовлено Алисой и как только
он завершил идентификацию он бы приготовил
копии состояний, которые получил от
Алисы. Таким образом, теорема о запрете
копирования явилась бы следствием того
факта, что достижимая информация об
этих состояниях строго меньше, чемН(p).
Можно обратить эти рассуждения и
показать, что из теоремы о запрете
клонирования следует, что достижимая
информация меньше чем Н(p).
Представим, что возможно клонировать
неортогональные состояния. После
получения состояния
![]() или
или![]() от Алисы, Боб смог бы повторно применить
клонирующее устройство для получения
состояния
от Алисы, Боб смог бы повторно применить
клонирующее устройство для получения
состояния![]() или
или![]() .
В пределе большихn
эти два состояния становятся практически
ортогональными и возможно различить
их с произвольной точностью при
проективных измерениях.
.
В пределе большихn
эти два состояния становятся практически
ортогональными и возможно различить
их с произвольной точностью при
проективных измерениях.