Файл: деп_тукс_10_11.doc

Энтропия фон Неймана, определяемая через матрицу плотности, согласно (2.12), в отличие от энтропии Шеннона, инвариантна относительно выбора представления матрицы плотности. Из (2.12) видно, что

.

Итак, классическая (шенноновская) энтропия дает меру неопределенности, связанную с классическим распределением вероятностей. Квантовые состояния описываются схожим образом, только вместо распределения вероятностей используются операторы плотности: В теории информации логарифмы принято брать по основанию “2”, в отличие от статистической физике, где используется по основанию “е” - “наты”.

Как и для энтропии Шеннона, полезно ввести квантовый аналог относительной энтропии. Пусть r и s -два оператора плотности. Относительной энтропией состояний (операторов) r и s (r относительно s) называется величина:

Как и соответствующая классическая величина, квантовая относительная энтропия может принимать бесконечные значения.

Так, относительная энтропия определяется как бесконечная, если ядро (kernel) оператора s (векторное пространство собственных векторов s с нулевыми собственными значениями) имеет нетривиальное пересечение с основанием (support) оператора r (векторное пространство образованное собственными векторами r с ненулевыми собственными значениями). В других случаях относительная энтропия конечна.

Квантовая относительная энтропия неотрицательна (неравенство Клейна):

равенство достигается, когда r = s.

Основные свойства энтропии фон Неймана.

1. Энтропия неотрицательна. Она принимает нулевые значения только для чистых состояний.

2. В N-мерном гильбертовом пространстве максимальное значение энтропии logN. Энтропия равна logN только если система находится в (полностью) смешанном состоянии I/d.

3. Предположим, что композиционная система AB находится в чистом состоянии. Тогда

S(A) = S(B)

4. Предположим, что p_i - это вероятности, а состояния r_i - раскладывается по собственным векторам с ненулевыми собственными значениями (имеют основание) в ортогональном базисе. Тогда

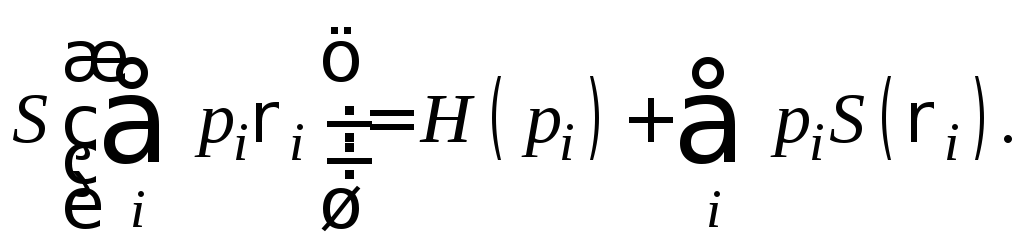
5. Теорема о совместной энтропии: предположим, что p_i - вероятности, 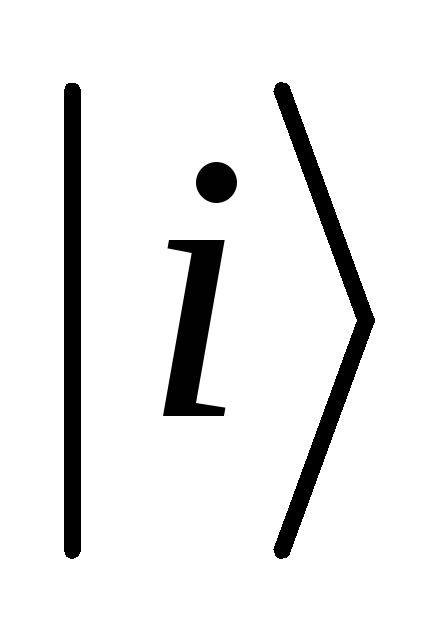- ортогональные состояния для системыА и r_i - любой набор операторов плотности для другой системы В, Тогда

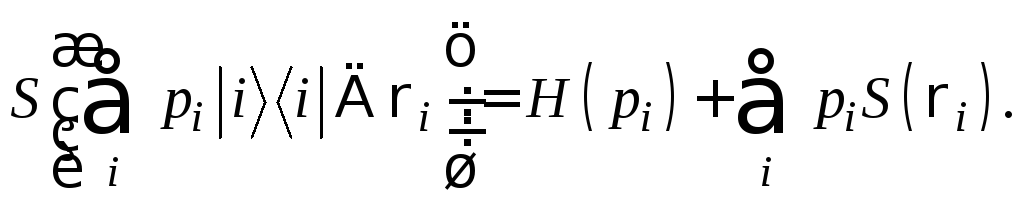
6. Субаддитивность энтропии . Пусть различные квантовые системы А и В имеют общее состояние r^АВ. Тогда совместная энтропия для двух систем удовлетворяет следующим неравенствам:

, причем равенство имеет место только если системы А и В некоррелированы, т.е.

- т.н. неравенство треугольника или Араки-Льеба. Это, фактически, квантовый аналог неравенства для энтропии Шеннона.

7. Вогнутость энтропии. Пусть p_i - неотрицательные действительные числа, такие, что 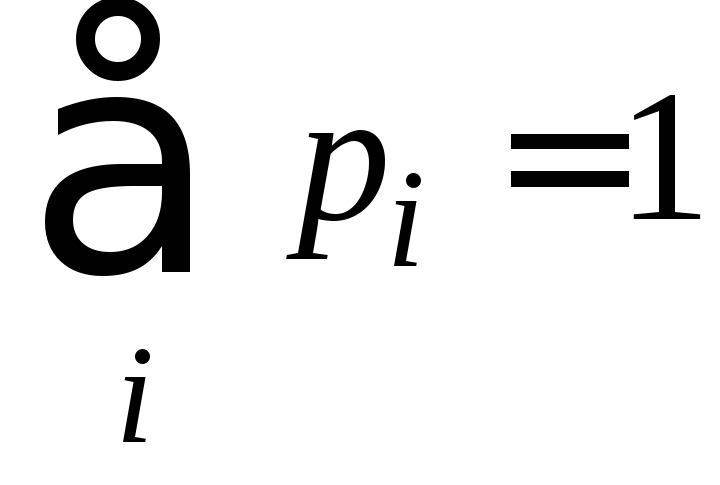, аr_i - соответствующие операторы плотности. Тогда энтропия удовлетворяет неравенству:

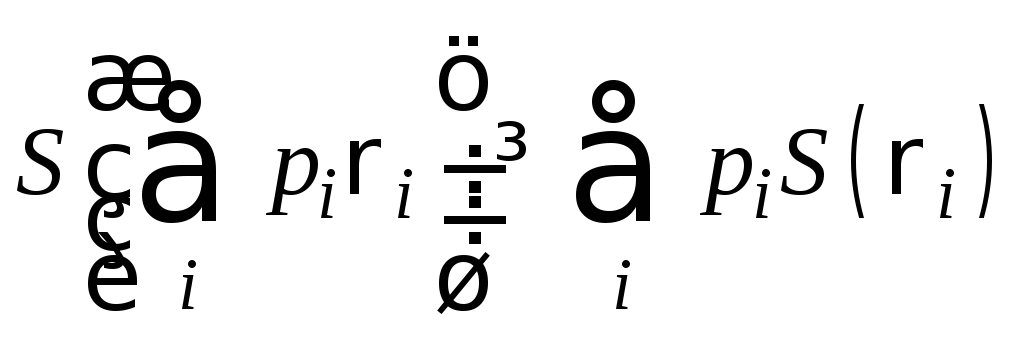- следует из св-ва (4).

Интуитивно ясно, что выражает состояние квантовой системы, которая находится в неизвестном состоянииr_i с вероятностью p_i. Неопределенность нашего знания о такой смеси состояний должна быть больше, чем средняя неопределенность состояний r_i, поскольку состояние дает вклад в неопределенность не только из-за наличия состоянийr_i но и благодаря усреднению по индексу i.

8. Энтропия смеси квантовых состояний. Обратная сторона условия вогнутости проявляется в некоей полезной теореме, дающей верхнюю границу для энтропии смеси квантовых состояний. А именно, что для смеси 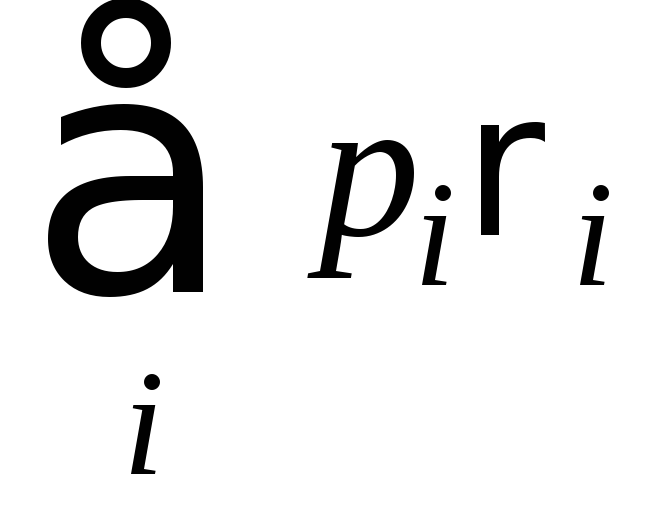квантовых состоянийr_i выполняется следующее неравенство:

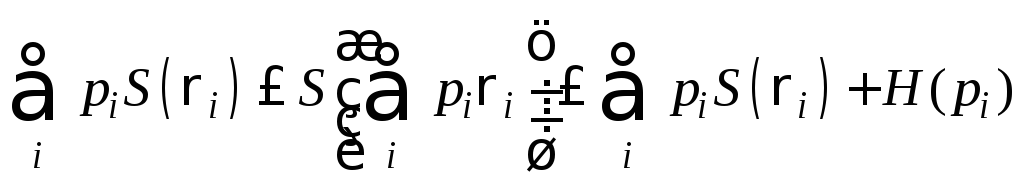
Что можно сказать о верхней границе или о правой части неравенства? Интуитивно ясно, что неопределенность состояния не может быть больше, чем средняя неопределенность состоянияr_i плюс дополнительный вклад за счет H(p_i), который представляет собой максимально возможный вклад в неопределенность об индексе i в общую неопределенность Сформулируем теперь теорему о верхней границе

Теорема. Предположим, что , гдеp_i - некоторый набор вероятностей, а r_i - операторы плотности. Тогда

, (**)

причем равенство достигается, если состояния r_i образуют ортогональный набор.

По аналогии с классическим случаем (энтропия Шеннона) для композиционных систем можно определить квантовые совместную и условную энтропии, а также квантовую взаимную информацию. Совместная энтропия S(A, B) для композиционной системы, состоящей из двух компонент А и В, определяется как и в классике:

(2.14)

где - матрица плотности системыАВ.

В классическом случае условной энтропией называлась величина

, (2.15)

где во втором равенстве использовано понятие совместной вероятности

- есть вероятность того, что Х принимает значение х, а Y принимает значение y.

Из определения (2.15) следует, что S(Y|X) есть мера того, сколько информации, в среднем, оставалось бы в Y при условии, что было бы известно Х. Заметим, что всегда S(Y|X) £ S(Y) и обычно S(Y|X) ¹ S(Х|У).

Определим условную энтропию, как

(2.16)

Определим взаимную информацию, как

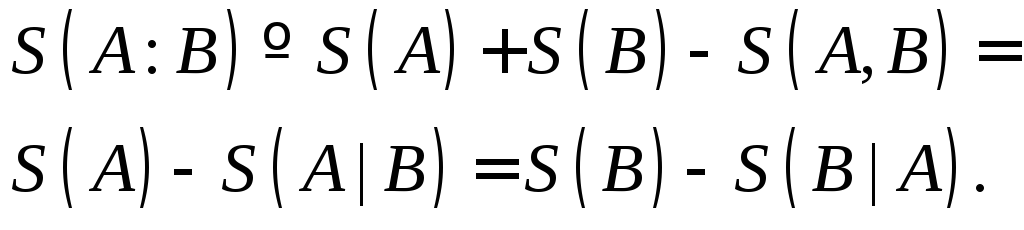(2.17)

Некоторые свойства энтропии Шеннона не переносятся на энтропию фон Неймана и отсюда следуют интересные следствия квантовой теории информации. Например, для случайных переменных X и Y имеет место неравенство: H(X) £ H(X, Y). Интуитивно, это понятно: не может быть большей неопределенности состояния X, чем для совместного состояния X и Y. Это интуитивное понимание не годится для квантовых состояний. Рассмотрим систему АВ двух кубитов в перепутанном состоянии :

. (2.18)

Это чистое состояние, поэтому S(A, B) = 0. С другой стороны, система А имеет оператор плотности I/2 (I - единичный оператор) и поэтому ее энтропия равна единице. Действительно, волновой функции состояния системы А (или В) (2.18) не существует, это состояние максимально смешанное. Другой способ интерпретации этого результата состоит в том, что для этой системы величина (условная энтропия) - отрицательная. Это соотношение может трактоваться как критерий перепутывания: если |АВ> - чистое состояние композиционной системы, то |АВ> находится в перепутанном состоянии если и только если S(A|B) < 0.

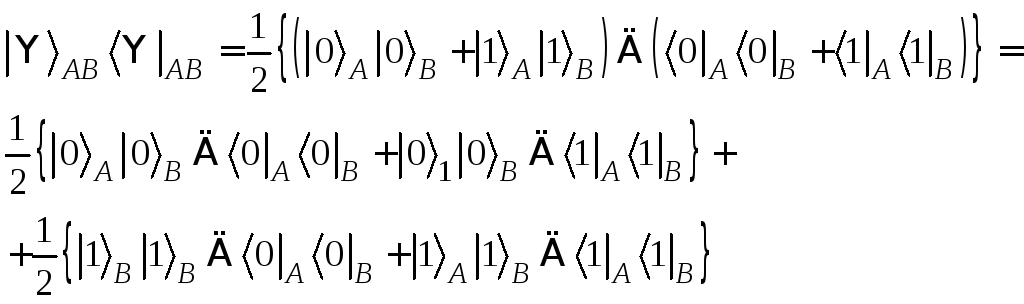
Тогда матрица плотности второй подсистемы

,

т.е. представляет собой взвешенную смесь. Следовательно, состояние второй подсистемы нельзя описывать волновой функцией; оно не является полностью определенным. Аналогично, матрица плотности первой подсистемы находится как след по индексам второй подсистемы:

.

Классическая теория информации, в основном, затрагивает проблему пересылки классических сообщений - букв алфавита, текстов, строк битов - через каналы связи, которые работают в соответствии с законами классической физики. Как изменится картина, если будут использоваться квантовые каналы связи? Можно ли передать информацию более эффективно? Можно ли использовать законы квантовой механики для того, чтобы передавать секретную информацию, защищенную от подслушивания? Такого рода вопросы возникают, когда мы используем каналы связи, работающие по законам квантовой механики. Такое переопределение того, что же есть канал связи вызвано необходимостью переосмысления основных положений классической теории информации .

Квантовая теория информации нацелена на исследование каналов связи, но она имеет гораздо более широкую область применения. Можно обозначить три фундаментальные цели, которые стоят перед теорией квантовой информации:

1. идентифицировать элементарные классы статических ресурсов в квантовой механике (или типы “информации”)

2. идентифицировать элементарные классы динамических процессов в квантовой механике (или типы информационных процессов)

3. характеризовать ресурсы, с помощью которых можно реализовать элементарные динамические процессы.

Оказывается, что квантовая теория информации гораздо глубже и богаче классической теории информации потому, что квантовая механика включает в себя гораздо больше элементарных классов статических и динамических ресурсов, которые не просто соответствуют известным классическим типам, но и описывают целые новые типы состояний, например, перепутанные состояния, которые не имеют аналога в классической физике.

Рассмотрим на некоторых примерах разницу в описании между квантовой и классической информацией.

По принципу соответствия “законы квантовой физики должны быть сформулированы таким образом, что в классических границах, когда в процесс вовлечено много квантов, эти законы приводили бы к классическим уравнениям для усредненных величин.” (Д.Бом).

Предположим, что Алиса имеет классический источник информации, который выдает символы X = 0, ... n с соответствующим распределением вероятностей p₀, ..., p_n. Цель Алисы и Боба состоит в том, чтобы Боб смог определить величину X наилучшим образом. Для того, чтобы достигнуть этого, Алиса приготавливает квантовое состояние r_Х выбирая его из некоторого фиксированного набора r₀,.... r_n, и посылает это состояние Бобу, который выполняет квантовое измерение над этим состоянием. Затем, он пытается сделать лучшее предположение о том, как идентифицировать X, основываясь над результатах своих измерений Y.

Хорошей мерой того, сколько информации получено Бобом о величине X из его измерений - это взаимная информация между X и результатом измерения Y. Боб может сделать заключение об X по результатам измерения Y только, если и только если H(X:Y) = H(X), и что в общем случае H(X:Y) £ H(X). Близость величины H(X:Y) к H(X) не самом деле дает хорошую меру того, как Боб смог определить Х. Цель Боба - выбрать измерение, которое максимизирует величину H(X:Y) и тем самым приближает ее к H(X). Для этого, определим достижимую информацию, как максимальную величину взаимной информации. Достижимая информация - это мера того, насколько хорошо Боб смог сделать вывод о приготовленном Алисой состоянии, которая она послала ему. Проиллюстрируем эти расссужденияследующим рисунком и сравнительной таблицей.