Файл: деп_тукс_10_11.doc

(2.11)

Для рассмотренного примера суммирование ведется по всем символам (буквам алфавита), а p_i означает вероятность появления символа с номером i. Как видно, это выражение охватывает как часто используемые буквы, так и буквы, вероятность появления которых в данном сообщении мала.

Поскольку в выражении (2.11) используется натуральный логарифм, соответствующую единицу информации называют “нат”.

Информационная энтропия - это мера недостатка (или степень неопределенности) информации о действительном состоянии физической системы.

Информационная энтропия Шеннона:

,

где

Это относится к двухуровневым системам, типа бит: “0” и “1”. Если размерность равна n, то H = log_n.

Так, для n = 3, Н = log₃, причем,  = 3.

Количество информации I (или просто информация) о состоянии классической системы, получаемое в результате измерений внешним прибором, связанным с рассматриваемой системой некоторым каналом связи, определяется как разность информационной энтропии, соответствующей начальной неопределенности состояния системы H₀, и информационной энтропии конечного состояния системы после измерения H. Таким образом,

I + H = H₀ = const.

В идеальном случае, когда отсутствуют шумы и помехи, создаваемые внешними источниками в канале связи, конечное распределение вероятностей после измерения сводится к одному определенному значению p_n = 1, т.е. H = 0, а максимальное значение полученной при измерении информации будет определяться : I_max = H₀. Таким образом, информационная энтропия Шеннона системы имеет смысл максимальной информации, заключенной в системе; она может быть определена в идеальных условиях измерения состояния системы в отсутствие шумов и помех, когда энтропия конечного состояния равна нулю, H = 0.

Рассмотрим классический логический элемент, который может находиться в одном из двух равновероятных логических состояний “0” и “1”. Переход элемента в одно из состояний, например, в состояние “0”, соответствует уменьшению статистического веса его состояния по сравнению с начальным состоянием в 2 раза (для трехуровневых систем - в 3 раза). Найдем уменьшение информационной энтропии Шеннона, которое соответствует увеличению количества информации об элементе на один бит:

Следовательно, информационная энтропия определяет число битов, которое требуется для кодирования информации в рассматриваемой системе или сообщении.

При обобщении энтропии Шеннона на квантовый случай (энтропию фон Неймана) необходимо определить оператор энтропии через оператор плотности :

S= - ln

Тогда, очевидно, физическая величина “энтропия” или S есть среднее значение этого оператора или по правилам вычисления средних величин в квантовой механике:

S= - ln = - Sp(ln )

Для рассмотрения процедуры вычисления логарифма оператора (недиагональные элементы матрицы плотности - вообще могут быть комплексными величинами, для которых логарифм не определен) рассмотрим две ситуации.

1. Чистое состояние. В этом случае возможно описание квантовой системы с помощью волновой функции в базисном представлении (т.е. как когерентную суперпозицию базисных состояний какого-нибудь оператора):

.

В этом случае, конечно, матрица плотности недиагональна. Наличие недиагональных элементов в базисном представлении как раз и отражает факт когерентности суперпозиции базисных состояний. Вообще же матрица плотности любой физической системы должна быть положительно определена, т.е. все ее собственные значения должны лежать в интервале [0,1]. Из линейной алгебры известно, что для любой эрмитовой матрицы А существует такая невырожденная матрица Т, что матрица является диагональной. Диагональные элементы матрицы в этом случае действительные и являются собственными значениями матрицыА. Более того, существует такая невырожденная матрица Т, что диагональные элементы - принимают только значения +1, -1 и/или 0.

Физически, матричное унитарное преобразование означает смену представления или базиса. Таким образом, чистое состояние системы всегда может быть представлено в виде собственного состояния какого-нибудь оператора. Например, рассмотрим когерентную суперпозицию двух состояний или кубит:

Пусть. Полным аналогом такого состояния является состояние поляризации света, когда поляризация составляет угол 45⁰ с вертикалью. Действительно, измерения поляризации отдельных фотонов в этом состоянии будут давать либо горизонтальную, либо вертикальную поляризации с вероятностью 1/2. В то же время измерения, проводимые в базисе +45⁰,всегда будут давать достоверный результат.

Эти рассуждения можно обобщить на случай произвольной (эллиптической) поляризации, когда в разложении волновой функции отличны от нуля два комплексных коэффициента.

Энтропия фон Неймана, определяемая через матрицу плотности, инвариантна относительно выбора базиса или представления, т.е., переходя к диагональному представлению,

. (2.12)

Но в чистом состоянии лишь один элемент матрицы плотности отличен от нуля, т.е. , а значит S = 0. Равенство нулю энтропии интерпретируется как минимальная неопределенность (хаотичность).

2. Смешанное состояние. Рассмотрим однородную смесь состояний: где, как обычно,Г - число состояний с данной энергией, т.е. микроканонический ансамбль Гиббса.

В смешанном состоянии недиагональные элементы матрицы плотности равны нулю - матрица имеет диагональный вид с диагональными элементами . Матрицу плотности смешанного состояния всегда можно привести к диагональному виду, но по диагонали будут стоять классические вероятности p₁......p_n.

Известно, что в диагональном представлении функции от операторов удовлетворяют соотношению:

,

где функционал F в данном случае - логарифм.

Тогда, ,

и из (2.12) следует, что

.

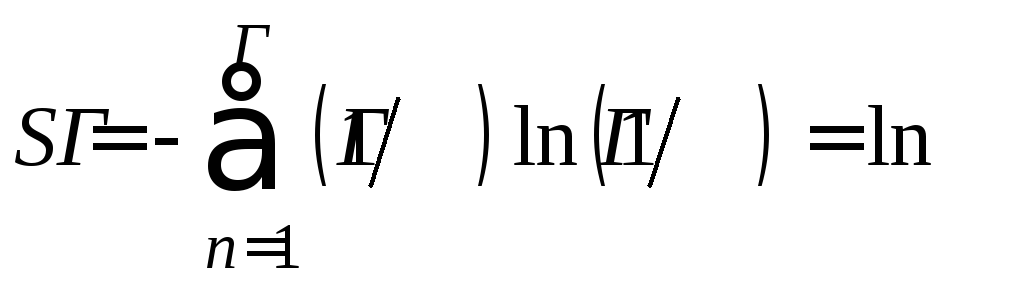Отсюда видно, что выполняется неравенство .

Рассмотрим двухуровневую систему

. (2.13)

Такой волновой функцией описываются, например, электронные или ядерные спины, двухуровневые атомы и прочее, иначе, это - кубит. Пусть основному состоянию атома приписывается значение собственного вектора |0>, а возбужденному - собственный вектор |1> (или значение проекции на ось z спина). Эти векторы в квантовой механике записываются в виде столбцов

Собственные “бра” векторы <| образуют эрмитово-сопряженные строки:

. Вектор состояния оканчивается на окружности единичного радиуса в двумерном гильбертовом пространстве. Измерение такого состояния состоит в определении коэффициентов разложения, или проекций измеряемого состояния на базисные состояния:

Собственному представлению оператора плотности двухуровневой системы, находящейся в чистом состоянии, соответствует диагональная матрица, выраженная через собственные векторы

,

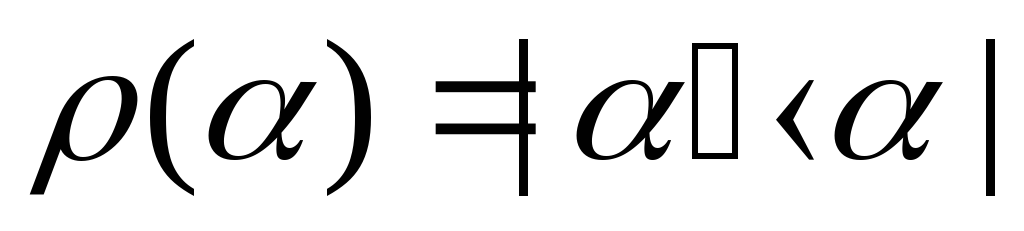причем двум возможным (собственным) состояниям отвечают следующие матрицы плотности:

. Т.о. для каждого  = 0, 1 у двухуровневой системы, находящейся в чистом состоянии, имеется только одно ненулевое значение матрицы, равное 1.

Для смешанного состояния и выбранного базиса матрица плотности имеет диагональный вид, поскольку недиагональные элементы, отвечающие за “когерентность” суперпозиции (2.13) равны нулю:

,

Отсюда сразу следует, что энтропия S совпадает с классической энтропией Шеннона случайной величины . Забегая вперед, можно сказать, что энтропия фон Неймана совпадает с энтропией Шеннона.

Рассмотрим когерентную суперпозицию (2.13). Тогда вектор ее состояния:

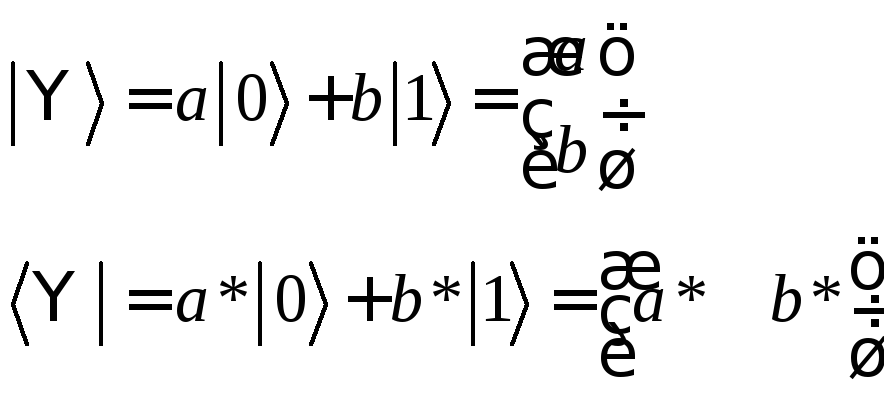
Матрица плотности чистого состояния уже недиагональна и в базисном представлении имеет вид:

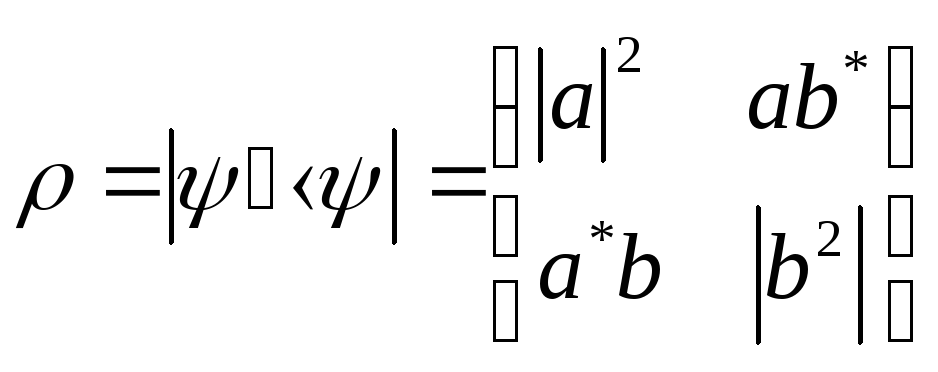(2.14)

Собственные значения матрицы находятся по правилу: пусть А - квадратная матрица , тогда любой векторх, из пространства Vⁿ для которого выполняется Ах=х называется собственным вектором, а  - собственным значением матрицы. Это уравнение эквивалентно уравнению (A-I)х = 0. Это однородная система линейных уравнений. Нетривиальные решения имеются тогда, когда определитель равен нулю:

det(A-I) = 0.

Или

.

Составим уравнение для собственных значений матрицы (2.14):

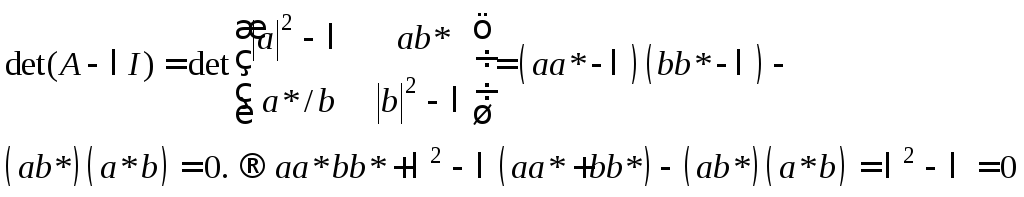
и, тогда .

Найдем энтропию Шеннона чистого состояния суперпозиции (2.13). Она совпадает с энтропией смешанного состояния с заданными классическими вероятностями заполнения или населенностями , поскольку не учитывает вклада недиагональных членов

Итак, энтропия Шеннона:

.

Максимальное значение эта величина достигает при , когда.

Отметим, что отличие матрицы плотности чистого состояния от смешанного состоит в том, что матрица плотности чистого состояния имеет только одно собственное значение, равное единице, в то время как для смешанного состояния у матрицы плотности отличны от нуля несколько собственных значений - т.н. парциальные (т.е. взвешенные с классическими вероятностями) населенности соответствующих чистых состояний.