Файл: Исаев Г Н Теоретико-методологические основы качества информационных систем.doc

В каждой строке таблицы ее элементы означают: 1-й – порядковый номер шага объединения, 2-й – значения отклонения между объединяемыми на данном шаге кластерами (евклидово расстояние), 3-й и 4-й – соответственно разность между средним значением каждой переменной по времени и стоимости и средневзвешенным значением образованного на данном шаге кластера, 5- й – суммарный вес реализаций в кластере, полученном на данном шаге. Дендрограмма отображена в соответствии с машинной распечаткой в виде древовидной горизонтальной схемы. Она содержит определенные сведения таблицы.

Слева от схемы помещены 3 столбца цифр. 1-й столбец указывает номера строк (реализаций) вводимых данных в ЭВМ из «Ведомости дефектов», 2-й – содержит коды дефектов, участвующих в кластеризации, 3-й – указывает последовательность объединения кластеров (дефектов) на каждом шаге.

Дендрограмма показывает, что на 497 шаге завершено объединение дефектов в классе по достоверности - дефекты с кодами 72,74,77,85,86 и др. На шаге 504 сформировался класс дефектов по полноте - коды 12,22, на шаге 514 сформировался класс дефектов по своевременности - код 3.

25 75 21

2 2 85 20

14 73 12

1 02 74 93

88 73 78

7 5 86 68

51 86 490

1 42 72 127

124 77 114

103 86 497

2 13 12 503

227 22 203

2 60 22 234

283 12 493

297 22 473

2 62 22 500

1 71 12 149

155 22 504

3 27 3 474

3 36 3 295

337 3 296

361 3 514

Рис. 4.1. Редуцированный вариант дендрограммы кластеризации дефектов автоматизированной обработки УБ

Анализ классификации позволяет установить, что внутри классов дефектов распределение модификаций дефектов равномерно. Можно предположить, что на уровне отдельного класса дефектов отсутствует какая-либо содержательная закономерность в распределении модификаций дефектов. Вместе с тем, очередность и характер объединения классов дефектов свидетельствуют о том, что сначала объединяются дефекты по достоверности, затем по полноте и, наконец, дефекты по своевременности, что подтверждает выдвинутые ранее предположения. Более конкретное представление о значимости каждого класса дефектов можно получить путем дальнейшей обработки статистической структуры по каждому классу дефектов в отдельности и в комплексе.

Оценка параметров ИС выполняется посредством реализации соответствующей программы статистического анализа данных. На машинном уровне исходные данные могут быть представлены массивами: массив А – данные по дефектам достоверности, массив В – по полноте, массив DE – по своевременности (таблица 4.17).

Для удобства анализа и оценки уровня качества, полученные на ЭВМ основные статистические данные, представляются по разработанной унифицированной форме в виде «Карты данных распределения дефектов» (КДРД) (таблицы 4.1-4.6). Под каждой таблицей приведены статистические характеристики. Эти характеристики получены путем расчета на ЭВМ оценок описательной статистики, а также оценок по формулам моделей измерения и оценки качества ИС (глава 3).

Таблица 4.1

Карта данных распределения дефектов достоверности по времени

Границы интервалов (мин.)	Абсолютная частота (символ)	Относительная частота	Относительная накопленная частота
1-2	12	0,08	0,08
2-3	38	0,25	0,33
3-4	52	0,34	0,67
4-5	34	0,22	0,89
5-6	13	0,08	0,97
6-7	5	0,03	1

Объем выборки: документов – 200, символов – 100000,

Среднее выборочное:

Среднее квадратическое отклонение:  = 1,188

Границы доверительного интервала среднего выборочного: нижняя – 2,895, верхняя – 3,274;

Вероятность дефекта  = 154/100000 = 0,00154

Показатель достоверности  = 1- 0,00154 = 0,99846

Оценка математического ожидания дефекта X=* = 3,084*0,00154 = 0,0047493 мин.

Таблица 4.2

Карта данных распределения дефектов полноты по времени

Границы интервалов (мин.)	Абсолютная час-тота(показатели)	Относительная частота	Относительная накопленная частота
1	2	3	4
6-7	5	0,03	0,03
7-8	7	0,04	0,07
8-9	10	0,06	0,13
9-10	16	0,1	0,23
10-11	20	0,12	0,35
11-12	25	0,16	0,51
12-13	24	0,14	0,65
13-14	21	0,13	0,78
14-15	15	0,09	0,87
15-16	9	0,05	0,92
16-17	7	0,04	0,96
17-18	7	0,04	1

Объем выборки: документов – 250, показателей – 6250.

Среднее выборочное: = 11,536.

Среднее квадратическое отклонение  = 2,671.

Границы доверительного интервала среднего выборочного: нижняя – 10,177, верхняя – 13,014.

Вероятность дефекта  = 166/6250 = 0,02656.

Показатель полноты _ = 1 – 0,02656 = 0,973444.

Оценка математического ожидания дефекта:

X = *  = 11,536 * 0,02656 = 0,3063961 мин.

Таблица 4.3

Карта данных распределения дефектов по своевременности на этапах 1 и 3

Границы интервалов (мин.)	Абсолютная частота (пачка)	Относительная частота	Накопленная частота
492-984	8	0,04	0,04
984-1476	13	0,07	0,11
1476-1968	19	0,1	0,21
1968-2460	29	0,15	0,36
2460-2952	44	0,23	0,59
2952-3444	30	0,15	0,74
3444-3936	26	0,13	0,87
3936-4428	15	0,08	0,95
4428-4920	9	0,04	0,99
4920-5412	2	0,01	1

Объем выборки: пачек документов – 269, среднее количество документов в пачке – 46, всего документов - 12374.

Среднее выборочное пачки: = 2548,30769.

Среднее квадратичное отклонение  = 1003,28.

Границы доверительного интервала среднего выборочного: нижняя – 27,11, верхняя – 3016,32.

Вероятность дефекта (пачки документов):  = 195/269 = 0,724907.

Показатель своевременности _s = 1 – 0,724907 = 0,275093.

Оценка математического ожидания дефекта

X = *  = 2548,30769 * 0,724907 = 1847,286 мин.

Оценка по документу – 40,158391 мин.

Таблица 4.4

Карта данных распределения дефектов достоверности по стоимости

Границы интервалов (коп.)	Абсолютная ча-стота (символы)	Относитель-ная частота	Относительная на-копленная частота
13-26	12	0,08	0,08
26-39	38	0,25	0,33
39-52	52	0,34	0,67
52-65	34	0,22	0,89
65-78	13	0,08	0,97
78-81	5	0,03	1

Объем выборки: документов – 200, показателей – 100000.

Среднее выборочное: = 40,175.

Среднее квадратическое отклонение  = 15,494.

Границы доверительного интервала среднего выборочного: нижняя – 37,708, верхняя – 42,642.

Вероятность дефекта  = 154/100000 = 0,00154.

Показатель достоверности _d = 1 – 0,00154 = 0,99846.

Оценка математического ожидания дефекта

X = *  = 40,175* 0,00154 = 0,0618695 коп.

Таблица 4.5

Карта данных распределения дефектов полноты по стоимости

Границы интервалов (коп.)	Абсолютная ча-стота (показатель)	Относитель-ная частота	Накопленная относительная частота
168-196	5	0,03	0,03
196-224	7	0,04	0,07
224-252	10	0,06	0,13
252-280	11	0,1	0,23
280-308	20	0,12	0,35
308-336	25	0,16	0,51
336-364	24	0,14	0,65
364-392	21	0,13	0,78
392-420	15	0,09	0,87
420-448	9	0,05	0,92
448-476	7	0,04	0,96
476-504	7	0,04	1

Объем выборки: пачек документов – 250, показателей 6250.

Среднее выборочное: = 323,009.

Среднее квадратическое отклонение  = 74,792.

Границы доверительного интервала среднего выборочного: нижняя –321,545, верхняя –334,473.

Вероятность дефекта:  = 166/6250 = 0,02656.

Показатель полноты _p = 1 – 0,02656 = 0,97344.

Оценка математического ожидания дефекта

X = *  = 323,009* 0,02656 = 8,579119 коп.

Таблица 4.6

Карта данных распределения дефектов своевременности

по стоимости на этапах 1 и 3

Границы интервалов (коп.)	Абсолютная частота (пачка)	Относитель-ная частота	Накопленная относительная частота
1	2	3	4
6396-12792	8	0,04	0,04
12792-19188	13	0,07	0,11
19188-25584	19	0,1	0,21
25584-31980	29	0,15	0,36
31980-38376	44	0,23	0,59
38376-44772	32	0,15	0,74
44772-51168	26	0,13	0,87
51168-57564	15	0,08	0,95
57564-63960	9	0,04	0,99
63960-70356	2	0,01	1

Объем выборки: пачек документов – 269, среднее количество документов

в пачке – 46, документов - 12374.

Среднее выборочное пачки: = 33126,0.

Среднее квадратическое отклонение  = 13044,0.

Границы доверительного интервала среднего выборочного: нижняя –13206,0, верхняя – 78366,0.

Вероятность дефекта:  = 195/269 = 0,724907.

Показатель своевременности _s = 1 – 0,724907 = 0,275093.

Оценка математического ожидания дефекта

X = *  = 33126,0* 0,724907 = 24013,269.

Оценка по документу – 522,02758 коп.

Графики распределения дефектов по времени отображены на рис. 4.2 – 4.4. По оси абсцисс отмечена ширина интервалов по времени. На рис. 4.4 время выражено в часах, на остальных графиках – в минутах. По оси ординат указано слева от оси количество дефектов, а справа относительная частота попадания дефектов в соответствующий интервал. Карты данных распределения дефектов достаточно наглядно отображают результаты сбора и обработки экспериментальных данных, необходимые для расчета значений показателей комплексной оценки качества. При первом приближении видно, что такие параметры как средние квадратические отклонения довольно существенно отличаются по достоверности, полноте и своевременности как относительно параметров времени, так и параметров стоимости. Если среднее выборочное по достоверности равно 3,084 мин., по полноте – 11,536 мин., то по своевременности это значение равно 2548,30 мин. Отсюда видно, что факторы-дефекты по своевременности являются доминирующими в общей структуре факторов-дефектов, снижающих качество обработки УБ.

В соответствии с моделями регрессии обобщенных показателей на основе полученных оценок могут быть составлены две матрицы фиксированных данных соответственно по производительности и себестоимости обработки УБ. Обработка матриц выполняется посредством программы регрессионного анализа. Регрессионный анализ зависимости обобщенных показателей от факторов-дефектов обработки выполняется путем применения соответствующей программы статистического анализа данных. В результате реализации регрессионной модели определяются

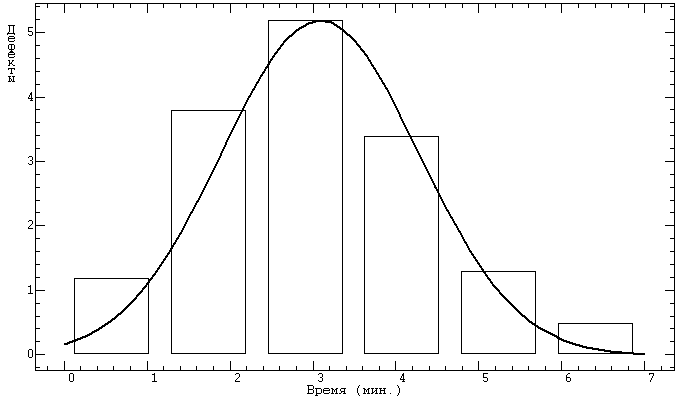
Рис. 4.2. Гистограмма распределения дефектов достоверности по времени

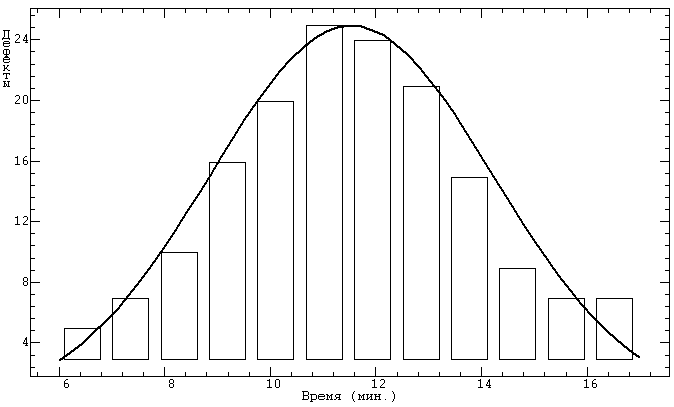
Рис.4.3. Гистограмма распределения дефектов полноты по времени

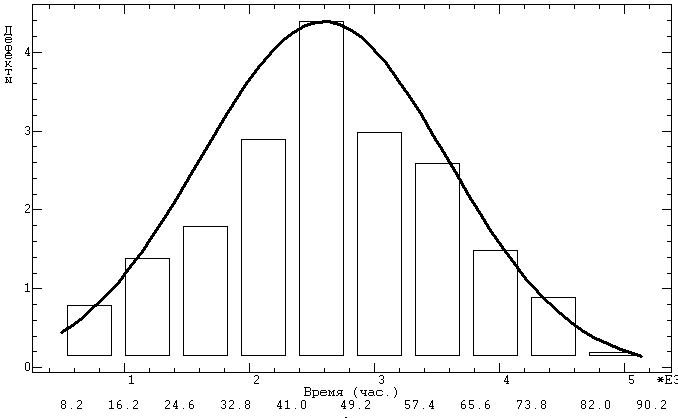
Рис. 4.4. Гистограмма распределения дефектов своевременности по времени

коэффициенты весомости по факторам-дефектам. На основе полученных оценок по достоверности, полноте и своевременности производится расчет значений матриц фиксированных данных соответственно по производительности и себестоимости (таблицы 4.7, 4.8). В этих таблицах в первых графах указаны значения процентов снижения значений переменных, указанные в графах 2-4 и значения прогнозируемых переменных в графах 5 таблиц. В таблице 4.7 предсказывающие переменные измеряются в человеко-днях, прогнозируемая переменная – в документо/днях, а в таблице 4.8, соответственно – рублях и рублях/документ.

В результате обработки данных матриц построены соответствующие графики зависимости обобщенных показателей по производительности и себестоимости от дефектов обработки (рис. 4.5, 4.6). По оси абсцисс отмечены значения процентов снижения дефектов, а по оси ординат соответствующие значения прогнозируемых переменных. Путем нанесения точек, указанных значений (табл. 4.7, 4.8), и соответствующей линии регрессии получены графические модели прогнозирования обобщенных показателей от снижения дефектов по соответствующим значениям процентов.

В практической работе оперативного управления качеством ИС на основе графиков можно получать экспресс-оценки прогнозируемой величины снижения (увеличения) соответственно по производительности и (или) себестоимости. Если необходимо определить, например, прогнозируемое значение обобщенного показателя по производительности ИС при условии снижения дефектов до 10%, то это значение будет равно ориентировочно 215 документов в день (рис. 4.5), что вполне согласуется с данными таблицы 4.7. Определяется путем нанесения линий параллельно осям

Таблица 4.7.

Матрица фиксированных данных по производительности

Таблица 4.8

Матрица фиксированных данных по себестоимости

Значение %	Достоверность (руб.)	Полнота (руб.)	Своевременность (руб.)	Себестоимость (руб.на док.)
1	2	3	4	5
0	15776,72	109383,76	266067,02	11,24
1	15618,95	108289,93	263406,06	11,17
2	15461,18	107196,10	260745,68	11,00
3	15303,42	106102,27	258085,01	11,02
4	15145,65	105008,44	255424,34	10,94
5	14987,88	103914,61	252763,67	10,86
6	14830,12	102820,78	250103,00	10,79
7	14672,35	101762,95	247442,33	10,71
8	14514,58	100633,12	244781,66	10,63
9	14356,81	99537,29	242120,99	10,56
10	14199,05	98445,45	239460,32	10,48
11	14041,28	97351,61	236799,65	10,40
12	13883,51	96257,77	234138,98	10,33
13	13725,75	95163,94	231478,31	10,25
14	13567,98	94070,10	228817,64	10,17
15	13410,21	92976,26	226156,97	10,09
16	13252,45	91882,43	223496,30	10,02
17	13094,68	90788,59	220835,63	9,94
18	12936,91	89694,75	218174,96	9,87
19	12779,14	88600,92	215514,29	9,79
20	12621,38	87507,08	212853,62	9,71